

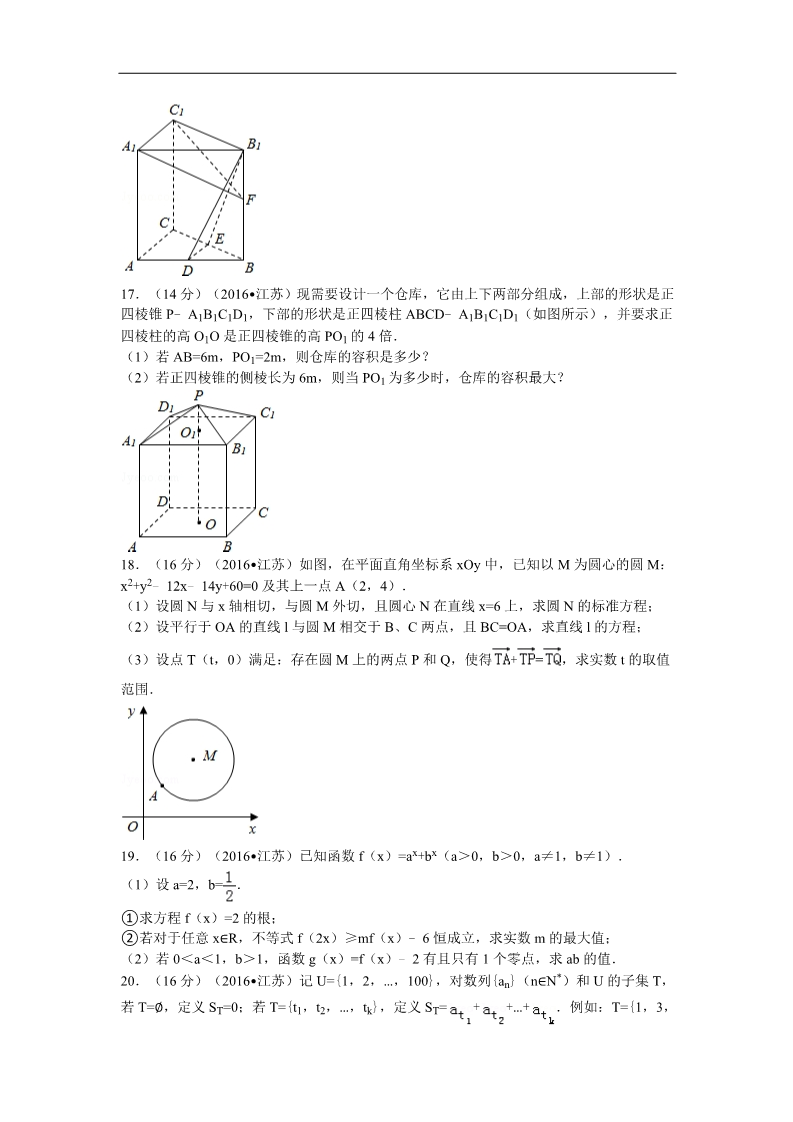
 2016 年江苏省高考数学试卷 一、填空题(共 14 小题,每小题 5 分,满分 70 分) 1.(5 分)(2016•江苏)已知集合 A={﹣1,2,3,6},B={x|﹣2<x<3},则 A∩B=______ .2.(5 分)(2016•江苏)复数 z=(1+2i)(3﹣i),其中 i 为虚数单位,则 z 的实部是______ .3.(5 分)(2016•江苏)在平面直角坐标系 xOy 中,双曲线 ﹣=1 的焦距是______. 4.(5 分)(2016•江苏)已知一组数据 4.7,4.8,5.1,5.4,5.5,则该组数据的方差是______ .5.(5 分)(2016•江苏)函数 y= 的定义域是______. 6.(5 分)(2016•江苏)如图是一个算法的流程图,则输出的 a 的值是______. 7.(5 分)(2016•江苏)将一颗质地均匀的骰子(一种各个面上分别标有 1,2,3,4,5, 6 个点的正方体玩具)先后抛掷 2 次,则出现向上的点数之和小于 10 的概率是______. 28.(5 分)(2016•江苏)已知{an}是等差数列,Sn 是其前 n 项和,若 a1+a2 =﹣3,S5=10, 则 a9 的值是______. 9.(5 分)(2016•江苏)定义在区间[0,3π]上的函数 y=sin2x 的图象与 y=cosx 的图象的 交点个数是______. 10.(5 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,F 是椭圆 +=1(a>b> 0)的右焦点,直线 y= 与椭圆交于 B,C 两点,且∠BFC=90°,则该椭圆的离心率是______ .11.(5 分)(2016•江苏)设 f(x)是定义在 R 上且周期为 2 的函数,在区间[﹣1,1)上 ,f(x)= ,其中 a∈R,若 f(﹣ )=f( ),则f(5a)的值是______ .12.(5 分)(2016•江苏)已知实数 x,y 满足 ______. ,则 x2+y2 的取值范围是 13.(5 分)(2016•江苏)如图,在△ABC 中,D 是 BC 的中点,E,F 是 AD 上的两个三 等分点, =4, =﹣1,则 的值是______. •••14.(5 分)(2016•江苏)在锐角三角形 ABC 中,若 sinA=2sinBsinC,则 tanAtanBtanC 的 最小值是______. 二、解答题(共 6 小题,满分 90 分) 15.(14 分)(2016•江苏)在△ABC 中,AC=6,cosB= ,C= (1)求 AB 的长; .(2)求 cos(A﹣ )的值. 16.(14 分)(2016•江苏)如图,在直三棱柱 ABC﹣A1B1C1 中,D,E 分别为 AB,BC 的中点,点 F 在侧棱 B1B 上,且 B1D⊥A1F,A1C1⊥A1B1.求证: (1)直线 DE∥平面 A1C1F; (2)平面 B1DE⊥平面 A1C1F. 17.(14 分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正 四棱锥 P﹣A1B1C1D1,下部的形状是正四棱柱 ABCD﹣A1B1C1D1(如图所示),并要求正 四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. (1)若 AB=6m,PO1=2m,则仓库的容积是多少? (2)若正四棱锥的侧棱长为 6m,则当 PO1 为多少时,仓库的容积最大? 18.(16 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知以 M 为圆心的圆 M: x2+y2﹣12x﹣14y+60=0 及其上一点 A(2,4). (1)设圆 N 与 x 轴相切,与圆 M 外切,且圆心 N 在直线 x=6 上,求圆 N 的标准方程; (2)设平行于 OA 的直线 l 与圆 M 相交于 B、C 两点,且 BC=OA,求直线 l 的方程; (3)设点 T(t,0)满足:存在圆 M 上的两点 P 和 Q,使得 +=,求实数 t 的取值 范围. 19.(16 分)(2016•江苏)已知函数 f(x)=ax+bx(a>0,b>0,a≠1,b≠1). (1)设 a=2,b= .①求方程 f(x)=2 的根; ②若对于任意 x∈R,不等式 f(2x)≥mf(x)﹣6 恒成立,求实数 m 的最大值; (2)若 0<a<1,b>1,函数 g(x)=f(x)﹣2 有且只有 1 个零点,求 ab 的值. 20.(16 分)(2016•江苏)记 U={1,2,…,100},对数列{an}(n∈N*)和 U 的子集 T, 若 T=∅,定义 ST=0;若 T={t1,t2,…,tk},定义 ST= ++…+ .例如:T={1,3, 66}时,ST=a1+a3+a66.现设{an}(n∈N*)是公比为 3 的等比数列,且当 T={2,4}时,ST=30 .(1)求数列{an}的通项公式; (2)对任意正整数 k(1≤k≤100),若 T⊆{1,2,…,k},求证:ST<ak+1 ;(3)设 C⊆U,D⊆U,SC≥SD,求证:SC+SC∩D≥2SD. 附加题【选做题】本题包括 A、B、C、D 四小题,请选定其中两小题,并在相应的答题区 域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算 步骤.A.【选修 4—1 几何证明选讲】 21.(10 分)(2016•江苏)如图,在△ABC 中,∠ABC=90°,BD⊥AC,D 为垂足,E 为 BC 的中点,求证:∠EDC=∠ABD. B.【选修 4—2:矩阵与变换】 22.(10 分)(2016•江苏)已知矩阵 A= ,矩阵 B 的逆矩阵 B﹣1 =,求 矩阵 AB. C.【选修 4—4:坐标系与参数方程】 23.(2016•江苏)在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参 数),椭圆 C 的参数方程为 点,求线段 AB 的长. (θ 为参数),设直线 l 与椭圆 C 相交于 A,B 两 24.(2016•江苏)设 a>0,|x﹣1|< ,|y﹣2|< ,求证:|2x+y﹣4|<a. 附加题【必做题】 25.(10 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知直线 l:x﹣y﹣2=0, 抛物线 C:y2=2px(p>0). (1)若直线 l 过抛物线 C 的焦点,求抛物线 C 的方程; (2)已知抛物线 C 上存在关于直线 l 对称的相异两点 P 和 Q. ①求证:线段 PQ 的中点坐标为(2﹣p,﹣p); ②求 p 的取值范围. 26.(10 分)(2016•江苏)(1)求 7C ﹣4C 的值; (2)设 m,n∈N*,n≥m,求证:(m+1)C +(m+2)C +(m+3) C+…+nC +(n+1)C =(m+1)C . 2016 年江苏省高考数学试卷 参考答案与试题解析 一、填空题(共 14 小题,每小题 5 分,满分 70 分) 1.(5 分)(2016•江苏)已知集合 A={﹣1,2,3,6},B={x|﹣2<x<3},则 A∩B= {﹣1 ,2} . 【分析】根据已知中集合 A={﹣1,2,3,6},B={x|﹣2<x<3},结合集合交集的定义可 得答案. 【解答】解:∵集合 A={﹣1,2,3,6},B={x|﹣2<x<3}, ∴A∩B={﹣1,2}, 故答案为:{﹣1,2} 【点评】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题. 2.(5 分)(2016•江苏)复数 z=(1+2i)(3﹣i),其中 i 为虚数单位,则 z 的实部是 5 .【分析】利用复数的运算法则即可得出. 【解答】解:z=(1+2i)(3﹣i)=5+5i, 则 z 的实部是 5, 故答案为:5. 【点评】本题考查了复数的运算性质,考查了推理能力与计算能力,属于基础题. 3.(5 分)(2016•江苏)在平面直角坐标系 xOy 中,双曲线 ﹣=1 的焦距是 2 .【分析】确定双曲线的几何量,即可求出双曲线 ﹣=1 的焦距. 【解答】解:双曲线 ﹣=1 中,a= ,b= ,∴c= =,∴双曲线 ﹣=1 的焦距是 2 .故答案为:2 .【点评】本题重点考查了双曲线的简单几何性质,考查学生的计算能力,比较基础. 4.(5 分)(2016•江苏)已知一组数据 4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 0.1 . 【分析】先求出数据 4.7,4.8,5.1,5.4,5.5 的平均数,由此能求出该组数据的方差. 【解答】解:∵数据 4.7,4.8,5.1,5.4,5.5 的平均数为: (4.7+4.8+5.1+5.4+5.5)=5.1, =∴该组数据的方差: S2= [(4.7﹣5.1)2+(4.8﹣5.1)2+(5.1﹣5.1)2+(5.4﹣5.1)2+(5.5﹣5.1)2]=0.1. 故答案为:0.1. 【点评】本题考查方差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运 用. 5.(5 分)(2016•江苏)函数 y= 的定义域是 [﹣3,1] . 【分析】根据被开方数不小于 0,构造不等式,解得答案. 【解答】解:由 3﹣2x﹣x2≥0 得:x2+2x﹣3≤0, 解得:x∈[﹣3,1], 故答案为:[﹣3,1] 【点评】本题考查的知识点是函数的定义域,二次不等式的解法,难度不大,属于基础题. 6.(5 分)(2016•江苏)如图是一个算法的流程图,则输出的 a 的值是 9 . 【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量 a 的值, 模拟程序的运行过程,可得答案. 【解答】解:当 a=1,b=9 时,不满足 a>b,故 a=5,b=7, 当 a=5,b=7 时,不满足 a>b,故 a=9,b=5 当 a=9,b=5 时,满足 a>b, 故输出的 a 值为 9, 故答案为:9 【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程 序法进行解答. 7.(5 分)(2016•江苏)将一颗质地均匀的骰子(一种各个面上分别标有 1,2,3,4,5, 6 个点的正方体玩具)先后抛掷 2 次,则出现向上的点数之和小于 10 的概率是 . 【分析】出现向上的点数之和小于 10 的对立事件是出现向上的点数之和不小于 10,由此利 用对立事件概率计算公式能求出出现向上的点数之和小于 10 的概率. 【解答】解:将一颗质地均匀的骰子(一种各个面上分别标有 1,2,3,4,5,6 个点的正 方体玩具)先后抛掷 2 次, 基本事件总数为 n=6×6=36, 出现向上的点数之和小于 10 的对立事件是出现向上的点数之和不小于 10, 出现向上的点数之和不小于 10 包含的基本事件有: (4,6),(6,4),(5,5),(5,6),(6,5),(6,6),共 6 个, ∴出现向上的点数之和小于 10 的概率: p=1﹣ = . 故答案为: .【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式 的合理运用. 28.(5 分)(2016•江苏)已知{an}是等差数列,Sn 是其前 n 项和,若 a1+a2 =﹣3,S5=10, 则 a9 的值是 20 . 【分析】利用等差数列的通项公式和前 n 项和公式列出方程组,求出首项和公差,由此能求 出 a9 的值. 2【解答】解:∵{an}是等差数列,Sn 是其前 n 项和,a1+a2 =﹣3,S5=10, ∴,解得 a1=﹣4,d=3, ∴a9=﹣4+8×3=20. 故答案为:20. 【点评】本题考查等差数列的第 9 项的求法,是基础题,解题时要认真审题,注意等差数列 的性质的合理运用. 9.(5 分)(2016•江苏)定义在区间[0,3π]上的函数 y=sin2x 的图象与 y=cosx 的图象的 交点个数是 7 . 【分析】画出函数 y=sin2x 与 y=cosx 在区间[0,3π]上的图象即可得到答案. 【解答】解:画出函数 y=sin2x 与 y=cosx 在区间[0,3π]上的图象如下: 由图可知,共 7 个交点. 故答案为:7. 【点评】本题考查正弦函数与余弦函数的图象,作出函数 y=sin2x 与 y=cosx 在区间[0,3π] 上的图象是关键,属于中档题. 10.(5 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,F 是椭圆 +=1(a>b> 0)的右焦点,直线 y= 与椭圆交于 B,C 两点,且∠BFC=90°,则该椭圆的离心率是 .【分析】设右焦点 F(c,0),将 y= 代入椭圆方程求得 B,C 的坐标,运用两直线垂直的 条件:斜率之积为﹣1,结合离心率公式,计算即可得到所求值. 【解答】解:设右焦点 F(c,0), 将 y= 代入椭圆方程可得 x=±a =± a, 可得 B(﹣ a, ),C( a, ), 由∠BFC=90°,可得 kBF•kCF=﹣1, 即有 •=﹣1, 化简为 b2=3a2﹣4c2, 由 b2=a2﹣c2,即有 3c2=2a2, 由 e= ,可得 e2= = , 可得 e= ,故答案为: .【点评】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为﹣1,考 查化简整理的运算能力,属于中档题. 11.(5 分)(2016•江苏)设 f(x)是定义在 R 上且周期为 2 的函数,在区间[﹣1,1)上 ,f(x)= ,其中 a∈R,若 f(﹣ )=f( ),则f(5a)的值是 ﹣ . 【分析】根据已知中函数的周期性,结合 f(﹣ )=f( ),可得a 值,进而得到 f(5a) 的值. 【解答】解:f(x)是定义在 R 上且周期为 2 的函数,在区间[﹣1,1)上,f(x)= ,∴f(﹣ )=f(﹣ )=﹣ +a, f( )=f( )=| ∴a= ﹣|= ,,∴f(5a)=f(3)=f(﹣1)=﹣1+ =﹣ 故答案为:﹣ ,【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出 a 值,是解答 的关键. 12.(5 分)(2016•江苏)已知实数 x,y 满足 ,则 x2+y2 的取值范围是 [ ,13] . 【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,结合两点间的距离公式 以及点到直线的距离公式进行求解即可. 【解答】解:作出不等式组对应的平面区域, 设 z=x2+y2,则 z 的几何意义是区域内的点到原点距离的平方, 由图象知 A 到原点的距离最大, 点 O 到直线 BC:2x+y﹣2=0 的距离最小, ,即 A(2,3),此时 z=22+32=4+9=13, 由得点 O 到直线 BC:2x+y﹣2=0 的距离 d= =,则 z=d2=( )2= ,故 z 的取值范围是[ ,13], 故答案为:[ ,13]. 【点评】本题主要考查线性规划的应用,涉及距离的计算,利用数形结合是解决本题的关键 . 13.(5 分)(2016•江苏)如图,在△ABC 中,D 是 BC 的中点,E,F 是 AD 上的两个三 等分点, •=4, •=﹣1,则 •的值是 . 【分析】由已知可得 +2 =+,=﹣ +,=+3 ,=﹣ +3 ,22=,=﹣ +2 ,结合已知求出 =,=,可得答案. 【解答】解:∵D 是 BC 的中点,E,F 是 AD 上的两个三等分点, ∴=+,=﹣ +,,=+3 ,=﹣ +3 2∴•=﹣2=﹣1, 2•=9 ﹣2=4, 22∴=,=,又∵ ∴=+2 ,=﹣ +2 ,22•=4 ﹣= , 故答案为: 【点评】本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档. 14.(5 分)(2016•江苏)在锐角三角形 ABC 中,若 sinA=2sinBsinC,则 tanAtanBtanC 的 最小值是 8 . 【分析】结合三角形关系和式子 sinA=2sinBsinC 可推出 sinBcosC+cosBsinC=2sinBsinC,进 而得到 tanB+tanC=2tanBtanC,结合函数特性可求得最小值. 【解答】解:由 sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC, 可得 sinBcosC+cosBsinC=2sinBsinC,① 由三角形 ABC 为锐角三角形,则 cosB>0,cosC>0, 在①式两侧同时除以 cosBcosC 可得 tanB+tanC=2tanBtanC, 又 tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣ ②, 则 tanAtanBtanC=﹣ •tanBtanC, 由 tanB+tanC=2tanBtanC 可得 tanAtanBtanC=﹣ ,令 tanBtanC=t,由 A,B,C 为锐角可得 tanA>0,tanB>0,tanC>0, 由②式得 1﹣tanBtanC<0,解得 t>1, tanAtanBtanC=﹣ =﹣ ,=( )2﹣ ,由 t>1 得,﹣ ≤<0, 因此 tanAtanBtanC 的最小值为 8, 当且仅当 t=2 时取到等号,此时 tanB+tanC=4,tanBtanC=2, 解得 tanB=2+ ,tanC=2﹣ ,tanA=4,(或 tanB,tanC 互换),此时 A,B,C 均为锐 角. 【点评】本题考查了三角恒等式的变化技巧和函数单调性知识,有一定灵活性. 二、解答题(共 6 小题,满分 90 分) 15.(14 分)(2016•江苏)在△ABC 中,AC=6,cosB= ,C= (1)求 AB 的长; .(2)求 cos(A﹣ )的值. 【分析】(1)利用正弦定理,即可求 AB 的长; (2)求出 cosA、sinA,利用两角差的余弦公式求 cos(A﹣ )的值. 【解答】解:(1)∵△ABC 中,cosB= ,∴sinB= ,∵,∴AB= =5 ;(2)cosA=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣ ∵A 为三角形的内角, .∴sinA= ,∴cos(A﹣ )= cosA+ sinA= .【点评】本题考查正弦定理,考查两角和差的余弦公式,考查学生的计算能力,属于基础题 . 16.(14 分)(2016•江苏)如图,在直三棱柱 ABC﹣A1B1C1 中,D,E 分别为 AB,BC 的中点,点 F 在侧棱 B1B 上,且 B1D⊥A1F,A1C1⊥A1B1.求证: (1)直线 DE∥平面 A1C1F; (2)平面 B1DE⊥平面 A1C1F. 【分析】(1)通过证明 DE∥AC,进而 DE∥A1C1,据此可得直线 DE∥平面 A1C1F1; (2)通过证明 A1F⊥DE 结合题目已知条件 A1F⊥B1D,进而可得平面 B1DE⊥平面 A1C1F. 【解答】解:(1)∵D,E 分别为 AB,BC 的中点, ∴DE 为△ABC 的中位线, ∴DE∥AC, ∵ABC﹣A1B1C1 为棱柱, ∴AC∥A1C1, ∴DE∥A1C1, ∵A1C1⊂平面 A1C1F,且 DE⊄平面 A1C1F, ∴DE∥A1C1F; (2)∵ABC﹣A1B1C1 为直棱柱, ∴AA1⊥平面 A1B1C1, ∴AA1⊥A1C1, 又∵A1C1⊥A1B1,且 AA1∩A1B1=A1,AA1、A1B1⊂平面 AA1B1B, ∴A1C1⊥平面 AA1B1B, ∵DE∥A1C1, ∴DE⊥平面 AA1B1B, 又∵A1F⊂平面 AA1B1B, ∴DE⊥A1F, 又∵A1F⊥B1D,DE∩B1D=D,且 DE、B1D⊂平面 B1DE, ∴A1F⊥平面 B1DE, 又∵A1F⊂平面 A1C1F, ∴平面 B1DE⊥平面 A1C1F. 【点评】本题考查直线与平面平行的证明,以及平面与平面相互垂直的证明,把握常用方法 最关键,难度不大. 17.(14 分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正 四棱锥 P﹣A1B1C1D1,下部的形状是正四棱柱 ABCD﹣A1B1C1D1(如图所示),并要求正 四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. (1)若 AB=6m,PO1=2m,则仓库的容积是多少? (2)若正四棱锥的侧棱长为 6m,则当 PO1 为多少时,仓库的容积最大? 【分析】(1)由正四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍,可得 PO1=2m 时,O1O=8m ,进而可得仓库的容积; (2)设 PO1=xm,则 O1O=4xm,A1O1= m,A1B1= •m,代入体积公 式,求出容积的表达式,利用导数法,可得最大值. 【解答】解:(1)∵PO1=2m,正四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. ∴O1O=8m, ∴仓库的容积 V= ×62×2+62×8=312m3, (2)若正四棱锥的侧棱长为 6m, 设 PO1=xm, 则 O1O=4xm,A1O1= m,A1B1= •m, 22则仓库的容积 V= ×( x<6), •)•x+( •)•4x= x3+312x,(0< ∴V′=﹣26×2+312,(0<x<6), 当 0<x<2 时,V′>0,V(x)单调递增; 当 2 <x<6 时,V′<0,V(x)单调递减; 故当 x=2 时,V(x)取最大值; 即当 PO1=2 m时,仓库的容积最大. 【点评】本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档. 18.(16 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知以 M 为圆心的圆 M: x2+y2﹣12x﹣14y+60=0 及其上一点 A(2,4). (1)设圆 N 与 x 轴相切,与圆 M 外切,且圆心 N 在直线 x=6 上,求圆 N 的标准方程; (2)设平行于 OA 的直线 l 与圆 M 相交于 B、C 两点,且 BC=OA,求直线 l 的方程; (3)设点 T(t,0)满足:存在圆 M 上的两点 P 和 Q,使得 +=,求实数 t 的取值 范围. 【分析】(1)设 N(6,n),则圆 N 为:(x﹣6)2+(y﹣n)2=n2,n>0,从而得到 |7﹣n|=|n|+5,由此能求出圆 N 的标准方程. (2)由题意得 OA=2 ,kOA=2,设 l:y=2x+b,则圆心 M 到直线 l 的距离:d= 由此能求出直线 l 的方程. ,(3) =,即| |= ,2+2 ,又| |≤10,得 t∈[2﹣2 ,2+2 ], 对于任意 t∈[2﹣2 ],欲使 ,只需要作直线 TA 的平行线,使圆心到直 线的距离为 ,由此能求出实数 t 的取值范围. 【解答】解:(1)∵N 在直线 x=6 上,∴设 N(6,n), ∵圆 N 与 x 轴相切,∴圆 N 为:(x﹣6)2+(y﹣n)2=n2,n>0, 22又圆 N 与圆 M 外切,圆 M:x2+y2﹣12x﹣14y+60=0,即圆 M:((x﹣6)+(x﹣7)=25, ∴|7﹣n|=|n|+5,解得 n=1, ∴圆 N 的标准方程为(x﹣6)2+(y﹣1)2=1. (2)由题意得 OA=2 ,kOA=2,设 l:y=2x+b, 则圆心 M 到直线 l 的距离:d= =,则|BC|=2 =2 ,BC=2 ,即 2 =2 ,解得 b=5 或 b=﹣15, ∴直线 l 的方程为:y=2x+5 或 y=2x﹣15. (3) |= =,即 ,即| |=| |, |,又| |≤10,即 对于任意 t∈[2﹣2 ≤10,解得 t∈[2﹣2 ,2+2 ], ,2+2 ],欲使 ,此时,| |≤10, 只需要作直线 TA 的平行线,使圆心到直线的距离为 ,必然与圆交于 P、Q 两点,此时| |=| |,即 ,因此实数 t 的取值范围为 t∈[2﹣2 ,2+2 ],. 【点评】本题考查圆的标准方程的求法,考查直线方程的求法,考查实数的取值范围的求法 ,是中档题,解题时要认真审题,注意圆的性质的合理运用. 19.(16 分)(2016•江苏)已知函数 f(x)=ax+bx(a>0,b>0,a≠1,b≠1). (1)设 a=2,b= .①求方程 f(x)=2 的根; ②若对于任意 x∈R,不等式 f(2x)≥mf(x)﹣6 恒成立,求实数 m 的最大值; (2)若 0<a<1,b>1,函数 g(x)=f(x)﹣2 有且只有 1 个零点,求 ab 的值. 【分析】(1)①利用方程,直接求解即可.②列出不等式,利用二次函数的性质以及函 数的最值,转化求解即可. (2)求出 g(x)=f(x)﹣2=ax+bx﹣2,求出函数的导数,构造函数 h(x)= +,求出 g(x)的最小值为:g(x0).同理①若 g(x0)<0,g(x)至少有两个零点,与条 件矛盾.②若 g(x0)>0,利用函数 g(x)=f(x)﹣2 有且只有 1 个零点,推出 g(x0)=0 ,然后求解 ab=1. 【解答】解:函数 f(x)=ax+bx(a>0,b>0,a≠1,b≠1). (1)设 a=2,b= .①方程 f(x)=2;即: ②不等式 f(2x)≥mf(x)﹣6 恒成立,即 令 t= ,t≥2. =2,可得 x=0. ≥m( )﹣6 恒成立. 不等式化为:t2﹣mt+4≥0 在 t≥2 时,恒成立.可得:△≤0 或 即:m2﹣16≤0 或 m≤4, ∴m∈(﹣∞,4]. 实数 m 的最大值为:4. (2)g(x)=f(x)﹣2=ax+bx﹣2, g′(x)=axlna+bxlnb=ax[ +]lnb, 0<a<1,b>1 可得 ,令 h(x)= 因此,x0= +,则 h(x)是递增函数,而,lna<0,lnb>0, 时,h(x0)=0, 因此 x∈(﹣∞,x0)时,h(x)<0,axlnb>0,则 g′(x)<0. x∈(x0,+∞)时,h(x)>0,axlnb>0,则 g′(x)>0, 则 g(x)在(﹣∞,x0)递减,(x0,+∞)递增,因此 g(x)的最小值为:g(x0). ①若 g(x0)<0,x<loga2 时,ax> =2,bx>0,则 g(x)>0, 因此 x1<loga2,且 x1<x0 时,g(x1)>0,因此 g(x)在(x1,x0)有零点, 则 g(x)至少有两个零点,与条件矛盾. ②若 g(x0)>0,函数 g(x)=f(x)﹣2 有且只有 1 个零点,g(x)的最小值为 g(x0), 可得 g(x0)=0, 由 g(0)=a0+b0﹣2=0, 因此 x0=0,因此 =0,﹣ =1,即 lna+lnb=0,ln(ab)=0,则 ab=1. 可得 ab=1. 【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒 成立的应用,考查分析问题解决问题的能力. 20.(16 分)(2016•江苏)记 U={1,2,…,100},对数列{an}(n∈N*)和 U 的子集 T, 若 T=∅,定义 ST=0;若 T={t1,t2,…,tk},定义 ST= ++…+ .例如:T={1,3, 66}时,ST=a1+a3+a66.现设{an}(n∈N*)是公比为 3 的等比数列,且当 T={2,4}时,ST=30 .(1)求数列{an}的通项公式; (2)对任意正整数 k(1≤k≤100),若 T⊆{1,2,…,k},求证:ST<ak+1 (3)设 C⊆U,D⊆U,SC≥SD,求证:SC+SC∩D≥2SD. ;【分析】(1)根据题意,由 ST 的定义,分析可得 ST=a2+a4=a2+9a2=30,计算可得 a2=3,进 而可得 a1 的值,由等比数列通项公式即可得答案; (2)根据题意,由 ST 的定义,分析可得 ST≤a1+a2+…ak=1+3+32+…+3k﹣1,由等比数列的前 n 项和公式计算可得证明; (3)设 A=∁C(C∩D),B=∁D(C∩D),则 A∩B=∅,进而分析可以将原命题转化为证明 SC ≥2SB,分 2 种情况进行讨论:①、若 B=∅,②、若 B≠∅,可以证明得到 SA≥2SB,即可 得证明. 【解答】解:(1)当 T={2,4}时,ST=a2+a4=a2+9a2=30, 因此 a2=3,从而 a1= 故 an=3n﹣1 =1, ,(2)ST≤a1+a2+…ak=1+3+32+…+3k﹣1 =<3k=ak+1 ,(3)设 A=∁C(C∩D),B=∁D(C∩D),则 A∩B=∅, 分析可得 SC=SA+SC∩D,SD=SB+SC∩D,则 SC+SC∩D﹣2SD=SA﹣2SB, 因此原命题的等价于证明 SC≥2SB, 由条件 SC≥SD,可得 SA≥SB, ①、若 B=∅,则 SB=0,故 SA≥2SB, ②、若 B≠∅,由 SA≥SB 可得 A≠∅,设 A 中最大元素为 l,B 中最大元素为 m, 若 m≥l+1,则其与 SA<ai+1≤am≤SB 相矛盾, 因为 A∩B=∅,所以 l≠m,则 l≥m+1, SB≤a1+a2+…am=1+3+32+…+3m﹣1 =≤=,即 SA≥2SB, 综上所述,SA≥2SB, 故 SC+SC∩D≥2SD. 【点评】本题考查数列的应用,涉及新定义的内容,解题的关键是正确理解题目中对于新定 义的描述. 附加题【选做题】本题包括 A、B、C、D 四小题,请选定其中两小题,并在相应的答题区 域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算 步骤.A.【选修 4—1 几何证明选讲】 21.(10 分)(2016•江苏)如图,在△ABC 中,∠ABC=90°,BD⊥AC,D 为垂足,E 为 BC 的中点,求证:∠EDC=∠ABD. 【分析】依题意,知∠BDC=90°,∠EDC=∠C,利用∠C+∠DBC=∠ABD+∠DBC=90°,可 得∠ABD=∠C,从而可证得结论. 【解答】解:由 BD⊥AC 可得∠BDC=90°, 因为 E 为 BC 的中点,所以 DE=CE= BC, 则:∠EDC=∠C, 由∠BDC=90°,可得∠C+∠DBC=90°, 由∠ABC=90°,可得∠ABD+∠DBC=90°, 因此∠ABD=∠C,而∠EDC=∠C, 所以,∠EDC=∠ABD. 【点评】本题考查三角形的性质应用,利用∠C+∠DBC=∠ABD+∠DBC=90°,证得∠ABD= ∠C 是关键,属于中档题. B.【选修 4—2:矩阵与变换】 22.(10 分)(2016•江苏)已知矩阵 A= 矩阵 AB. ,矩阵 B 的逆矩阵 B﹣1 =,求 ﹣1 【分析】依题意,利用矩阵变换求得 B=(B﹣1 )==,再利用矩阵乘法的性 质可求得答案. 【解答】解:∵B﹣1 =,﹣1 ∴B=(B﹣1 )==,又 A= ,∴AB= =.【点评】本题考查逆变换与逆矩阵,考查矩阵乘法的性质,属于中档题. C.【选修 4—4:坐标系与参数方程】 23.(2016•江苏)在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参 数),椭圆 C 的参数方程为 点,求线段 AB 的长. (θ 为参数),设直线 l 与椭圆 C 相交于 A,B 两 【分析】分别化直线与椭圆的参数方程为普通方程,然后联立方程组,求出直线与椭圆的交 点坐标,代入两点间的距离公式求得答案. 【解答】解:由 ,由②得 ,代入①并整理得, .由,得 ,两式平方相加得 .联立 ,解得 或.∴|AB|= .【点评】本题考查直线与椭圆的参数方程,考查了参数方程化普通方程,考查直线与椭圆位 置关系的应用,是基础题. 24.(2016•江苏)设 a>0,|x﹣1|< ,|y﹣2|< ,求证:|2x+y﹣4|<a. 【分析】运用绝对值不等式的性质:|a+b|≤|a|+|b|,结合不等式的基本性质,即可得证. 【解答】证明:由 a>0,|x﹣1|< ,|y﹣2|< 可得|2x+y﹣4|=|2(x﹣1)+(y﹣2)| ,≤2|x﹣1|+|y﹣2|< + =a, 则|2x+y﹣4|<a 成立. 【点评】本题考查绝对值不等式的证明,注意运用绝对值不等式的性质,以及不等式的简单 性质,考查运算能力,属于基础题. 附加题【必做题】 25.(10 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知直线 l:x﹣y﹣2=0, 抛物线 C:y2=2px(p>0). (1)若直线 l 过抛物线 C 的焦点,求抛物线 C 的方程; (2)已知抛物线 C 上存在关于直线 l 对称的相异两点 P 和 Q. ①求证:线段 PQ 的中点坐标为(2﹣p,﹣p); ②求 p 的取值范围. 【分析】(1)求出抛物线的焦点坐标,然后求解抛物线方程. (2):①设点 P(x1,y1),Q(x2,y2),通过抛物线方程,求解 kPQ,通过 P,Q 关于 直线 l 对称,点的 kPQ=﹣1,推出 ,PQ 的中点在直线 l 上,推出 =2﹣p ,即可证明线段 PQ 的中点坐标为(2﹣p,﹣p); ②利用线段 PQ 中点坐标(2﹣p,﹣p).推出 ,得到关于 y2+2py+4p2﹣4p=0,有两个不相等的实数根,列出不等式即可求出 p 的范围. 【解答】解:(1)∵l:x﹣y﹣2=0,∴l 与 x 轴的交点坐标(2,0), 即抛物线的焦点坐标(2,0). ∴,∴抛物线 C:y2=8x. (2)证明:①设点 P(x1,y1),Q(x2,y2),则: ,即: ,kPQ ==,又∵P,Q 关于直线 l 对称,∴kPQ=﹣1,即 y1+y2=﹣2p,∴ ,又 PQ 的中点在直线 l 上,∴ ==2﹣p, ∴线段 PQ 的中点坐标为(2﹣p,﹣p); ②因为 Q 中点坐标(2﹣p,﹣p). ∴∴,即 ,即关于 y2+2py+4p2﹣4p=0,有两个不相等的实数根, ∴△>0,(2p)2﹣4(4p2﹣4p)>0, ∴p∈ .【点评】本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及 计算能力. 26.(10 分)(2016•江苏)(1)求 7C ﹣4C 的值; (2)设 m,n∈N*,n≥m,求证:(m+1)C +(m+2)C +…+nC +(n+1)C =(m+1)C 【分析】(1)由已知直接利用组合公式能求出 7 (2)对任意 m∈N*,当 n=m 时,验证等式成立;再假设 n=k(k≥m)时命题成立,推导出 +(m+3) C.的值. 当 n=k+1 时,命题也成立,由此利用数学归纳法能证明(m+1)C +(m+2)C )C +…+nC +(n+1)C =(m+1)C 【解答】解:(1)7 ﹣4× =7×20﹣4×35=0. +(m+3 .=证明:(2)对任意 m∈N*, ①当 n=m 时,左边=(m+1) =m+1, 右边=(m+1) =m+1,等式成立. ②假设 n=k(k≥m)时命题成立, 即(m+1)C +(m+2)C +(m+3)C +…+k +(k+1) =(m+1) +(k+1) +(k+2) ,当 n=k+1 时, 左边=(m+1) +(m+2) +(m+3) +=,右边= ∵=(m+1)[ =(m+1)× =(k+2) =(k+2) ∴﹣][k+3﹣(k﹣m+1)] ,=(m+1) ,∴左边=右边, ∴n=k+1 时,命题也成立, ∴m,n∈N*,n≥m,(m+1)C +(m+2)C +(m+3)C +…+nC +(n+1)C =(m+1)C .【点评】本题考查组合数的计算与证明,是中档题,解题时要认真审题,注意组合数公式和 数学归纳法的合理运用.
2016 年江苏省高考数学试卷 一、填空题(共 14 小题,每小题 5 分,满分 70 分) 1.(5 分)(2016•江苏)已知集合 A={﹣1,2,3,6},B={x|﹣2<x<3},则 A∩B=______ .2.(5 分)(2016•江苏)复数 z=(1+2i)(3﹣i),其中 i 为虚数单位,则 z 的实部是______ .3.(5 分)(2016•江苏)在平面直角坐标系 xOy 中,双曲线 ﹣=1 的焦距是______. 4.(5 分)(2016•江苏)已知一组数据 4.7,4.8,5.1,5.4,5.5,则该组数据的方差是______ .5.(5 分)(2016•江苏)函数 y= 的定义域是______. 6.(5 分)(2016•江苏)如图是一个算法的流程图,则输出的 a 的值是______. 7.(5 分)(2016•江苏)将一颗质地均匀的骰子(一种各个面上分别标有 1,2,3,4,5, 6 个点的正方体玩具)先后抛掷 2 次,则出现向上的点数之和小于 10 的概率是______. 28.(5 分)(2016•江苏)已知{an}是等差数列,Sn 是其前 n 项和,若 a1+a2 =﹣3,S5=10, 则 a9 的值是______. 9.(5 分)(2016•江苏)定义在区间[0,3π]上的函数 y=sin2x 的图象与 y=cosx 的图象的 交点个数是______. 10.(5 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,F 是椭圆 +=1(a>b> 0)的右焦点,直线 y= 与椭圆交于 B,C 两点,且∠BFC=90°,则该椭圆的离心率是______ .11.(5 分)(2016•江苏)设 f(x)是定义在 R 上且周期为 2 的函数,在区间[﹣1,1)上 ,f(x)= ,其中 a∈R,若 f(﹣ )=f( ),则f(5a)的值是______ .12.(5 分)(2016•江苏)已知实数 x,y 满足 ______. ,则 x2+y2 的取值范围是 13.(5 分)(2016•江苏)如图,在△ABC 中,D 是 BC 的中点,E,F 是 AD 上的两个三 等分点, =4, =﹣1,则 的值是______. •••14.(5 分)(2016•江苏)在锐角三角形 ABC 中,若 sinA=2sinBsinC,则 tanAtanBtanC 的 最小值是______. 二、解答题(共 6 小题,满分 90 分) 15.(14 分)(2016•江苏)在△ABC 中,AC=6,cosB= ,C= (1)求 AB 的长; .(2)求 cos(A﹣ )的值. 16.(14 分)(2016•江苏)如图,在直三棱柱 ABC﹣A1B1C1 中,D,E 分别为 AB,BC 的中点,点 F 在侧棱 B1B 上,且 B1D⊥A1F,A1C1⊥A1B1.求证: (1)直线 DE∥平面 A1C1F; (2)平面 B1DE⊥平面 A1C1F. 17.(14 分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正 四棱锥 P﹣A1B1C1D1,下部的形状是正四棱柱 ABCD﹣A1B1C1D1(如图所示),并要求正 四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. (1)若 AB=6m,PO1=2m,则仓库的容积是多少? (2)若正四棱锥的侧棱长为 6m,则当 PO1 为多少时,仓库的容积最大? 18.(16 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知以 M 为圆心的圆 M: x2+y2﹣12x﹣14y+60=0 及其上一点 A(2,4). (1)设圆 N 与 x 轴相切,与圆 M 外切,且圆心 N 在直线 x=6 上,求圆 N 的标准方程; (2)设平行于 OA 的直线 l 与圆 M 相交于 B、C 两点,且 BC=OA,求直线 l 的方程; (3)设点 T(t,0)满足:存在圆 M 上的两点 P 和 Q,使得 +=,求实数 t 的取值 范围. 19.(16 分)(2016•江苏)已知函数 f(x)=ax+bx(a>0,b>0,a≠1,b≠1). (1)设 a=2,b= .①求方程 f(x)=2 的根; ②若对于任意 x∈R,不等式 f(2x)≥mf(x)﹣6 恒成立,求实数 m 的最大值; (2)若 0<a<1,b>1,函数 g(x)=f(x)﹣2 有且只有 1 个零点,求 ab 的值. 20.(16 分)(2016•江苏)记 U={1,2,…,100},对数列{an}(n∈N*)和 U 的子集 T, 若 T=∅,定义 ST=0;若 T={t1,t2,…,tk},定义 ST= ++…+ .例如:T={1,3, 66}时,ST=a1+a3+a66.现设{an}(n∈N*)是公比为 3 的等比数列,且当 T={2,4}时,ST=30 .(1)求数列{an}的通项公式; (2)对任意正整数 k(1≤k≤100),若 T⊆{1,2,…,k},求证:ST<ak+1 ;(3)设 C⊆U,D⊆U,SC≥SD,求证:SC+SC∩D≥2SD. 附加题【选做题】本题包括 A、B、C、D 四小题,请选定其中两小题,并在相应的答题区 域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算 步骤.A.【选修 4—1 几何证明选讲】 21.(10 分)(2016•江苏)如图,在△ABC 中,∠ABC=90°,BD⊥AC,D 为垂足,E 为 BC 的中点,求证:∠EDC=∠ABD. B.【选修 4—2:矩阵与变换】 22.(10 分)(2016•江苏)已知矩阵 A= ,矩阵 B 的逆矩阵 B﹣1 =,求 矩阵 AB. C.【选修 4—4:坐标系与参数方程】 23.(2016•江苏)在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参 数),椭圆 C 的参数方程为 点,求线段 AB 的长. (θ 为参数),设直线 l 与椭圆 C 相交于 A,B 两 24.(2016•江苏)设 a>0,|x﹣1|< ,|y﹣2|< ,求证:|2x+y﹣4|<a. 附加题【必做题】 25.(10 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知直线 l:x﹣y﹣2=0, 抛物线 C:y2=2px(p>0). (1)若直线 l 过抛物线 C 的焦点,求抛物线 C 的方程; (2)已知抛物线 C 上存在关于直线 l 对称的相异两点 P 和 Q. ①求证:线段 PQ 的中点坐标为(2﹣p,﹣p); ②求 p 的取值范围. 26.(10 分)(2016•江苏)(1)求 7C ﹣4C 的值; (2)设 m,n∈N*,n≥m,求证:(m+1)C +(m+2)C +(m+3) C+…+nC +(n+1)C =(m+1)C . 2016 年江苏省高考数学试卷 参考答案与试题解析 一、填空题(共 14 小题,每小题 5 分,满分 70 分) 1.(5 分)(2016•江苏)已知集合 A={﹣1,2,3,6},B={x|﹣2<x<3},则 A∩B= {﹣1 ,2} . 【分析】根据已知中集合 A={﹣1,2,3,6},B={x|﹣2<x<3},结合集合交集的定义可 得答案. 【解答】解:∵集合 A={﹣1,2,3,6},B={x|﹣2<x<3}, ∴A∩B={﹣1,2}, 故答案为:{﹣1,2} 【点评】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题. 2.(5 分)(2016•江苏)复数 z=(1+2i)(3﹣i),其中 i 为虚数单位,则 z 的实部是 5 .【分析】利用复数的运算法则即可得出. 【解答】解:z=(1+2i)(3﹣i)=5+5i, 则 z 的实部是 5, 故答案为:5. 【点评】本题考查了复数的运算性质,考查了推理能力与计算能力,属于基础题. 3.(5 分)(2016•江苏)在平面直角坐标系 xOy 中,双曲线 ﹣=1 的焦距是 2 .【分析】确定双曲线的几何量,即可求出双曲线 ﹣=1 的焦距. 【解答】解:双曲线 ﹣=1 中,a= ,b= ,∴c= =,∴双曲线 ﹣=1 的焦距是 2 .故答案为:2 .【点评】本题重点考查了双曲线的简单几何性质,考查学生的计算能力,比较基础. 4.(5 分)(2016•江苏)已知一组数据 4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 0.1 . 【分析】先求出数据 4.7,4.8,5.1,5.4,5.5 的平均数,由此能求出该组数据的方差. 【解答】解:∵数据 4.7,4.8,5.1,5.4,5.5 的平均数为: (4.7+4.8+5.1+5.4+5.5)=5.1, =∴该组数据的方差: S2= [(4.7﹣5.1)2+(4.8﹣5.1)2+(5.1﹣5.1)2+(5.4﹣5.1)2+(5.5﹣5.1)2]=0.1. 故答案为:0.1. 【点评】本题考查方差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运 用. 5.(5 分)(2016•江苏)函数 y= 的定义域是 [﹣3,1] . 【分析】根据被开方数不小于 0,构造不等式,解得答案. 【解答】解:由 3﹣2x﹣x2≥0 得:x2+2x﹣3≤0, 解得:x∈[﹣3,1], 故答案为:[﹣3,1] 【点评】本题考查的知识点是函数的定义域,二次不等式的解法,难度不大,属于基础题. 6.(5 分)(2016•江苏)如图是一个算法的流程图,则输出的 a 的值是 9 . 【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量 a 的值, 模拟程序的运行过程,可得答案. 【解答】解:当 a=1,b=9 时,不满足 a>b,故 a=5,b=7, 当 a=5,b=7 时,不满足 a>b,故 a=9,b=5 当 a=9,b=5 时,满足 a>b, 故输出的 a 值为 9, 故答案为:9 【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程 序法进行解答. 7.(5 分)(2016•江苏)将一颗质地均匀的骰子(一种各个面上分别标有 1,2,3,4,5, 6 个点的正方体玩具)先后抛掷 2 次,则出现向上的点数之和小于 10 的概率是 . 【分析】出现向上的点数之和小于 10 的对立事件是出现向上的点数之和不小于 10,由此利 用对立事件概率计算公式能求出出现向上的点数之和小于 10 的概率. 【解答】解:将一颗质地均匀的骰子(一种各个面上分别标有 1,2,3,4,5,6 个点的正 方体玩具)先后抛掷 2 次, 基本事件总数为 n=6×6=36, 出现向上的点数之和小于 10 的对立事件是出现向上的点数之和不小于 10, 出现向上的点数之和不小于 10 包含的基本事件有: (4,6),(6,4),(5,5),(5,6),(6,5),(6,6),共 6 个, ∴出现向上的点数之和小于 10 的概率: p=1﹣ = . 故答案为: .【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式 的合理运用. 28.(5 分)(2016•江苏)已知{an}是等差数列,Sn 是其前 n 项和,若 a1+a2 =﹣3,S5=10, 则 a9 的值是 20 . 【分析】利用等差数列的通项公式和前 n 项和公式列出方程组,求出首项和公差,由此能求 出 a9 的值. 2【解答】解:∵{an}是等差数列,Sn 是其前 n 项和,a1+a2 =﹣3,S5=10, ∴,解得 a1=﹣4,d=3, ∴a9=﹣4+8×3=20. 故答案为:20. 【点评】本题考查等差数列的第 9 项的求法,是基础题,解题时要认真审题,注意等差数列 的性质的合理运用. 9.(5 分)(2016•江苏)定义在区间[0,3π]上的函数 y=sin2x 的图象与 y=cosx 的图象的 交点个数是 7 . 【分析】画出函数 y=sin2x 与 y=cosx 在区间[0,3π]上的图象即可得到答案. 【解答】解:画出函数 y=sin2x 与 y=cosx 在区间[0,3π]上的图象如下: 由图可知,共 7 个交点. 故答案为:7. 【点评】本题考查正弦函数与余弦函数的图象,作出函数 y=sin2x 与 y=cosx 在区间[0,3π] 上的图象是关键,属于中档题. 10.(5 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,F 是椭圆 +=1(a>b> 0)的右焦点,直线 y= 与椭圆交于 B,C 两点,且∠BFC=90°,则该椭圆的离心率是 .【分析】设右焦点 F(c,0),将 y= 代入椭圆方程求得 B,C 的坐标,运用两直线垂直的 条件:斜率之积为﹣1,结合离心率公式,计算即可得到所求值. 【解答】解:设右焦点 F(c,0), 将 y= 代入椭圆方程可得 x=±a =± a, 可得 B(﹣ a, ),C( a, ), 由∠BFC=90°,可得 kBF•kCF=﹣1, 即有 •=﹣1, 化简为 b2=3a2﹣4c2, 由 b2=a2﹣c2,即有 3c2=2a2, 由 e= ,可得 e2= = , 可得 e= ,故答案为: .【点评】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为﹣1,考 查化简整理的运算能力,属于中档题. 11.(5 分)(2016•江苏)设 f(x)是定义在 R 上且周期为 2 的函数,在区间[﹣1,1)上 ,f(x)= ,其中 a∈R,若 f(﹣ )=f( ),则f(5a)的值是 ﹣ . 【分析】根据已知中函数的周期性,结合 f(﹣ )=f( ),可得a 值,进而得到 f(5a) 的值. 【解答】解:f(x)是定义在 R 上且周期为 2 的函数,在区间[﹣1,1)上,f(x)= ,∴f(﹣ )=f(﹣ )=﹣ +a, f( )=f( )=| ∴a= ﹣|= ,,∴f(5a)=f(3)=f(﹣1)=﹣1+ =﹣ 故答案为:﹣ ,【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出 a 值,是解答 的关键. 12.(5 分)(2016•江苏)已知实数 x,y 满足 ,则 x2+y2 的取值范围是 [ ,13] . 【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,结合两点间的距离公式 以及点到直线的距离公式进行求解即可. 【解答】解:作出不等式组对应的平面区域, 设 z=x2+y2,则 z 的几何意义是区域内的点到原点距离的平方, 由图象知 A 到原点的距离最大, 点 O 到直线 BC:2x+y﹣2=0 的距离最小, ,即 A(2,3),此时 z=22+32=4+9=13, 由得点 O 到直线 BC:2x+y﹣2=0 的距离 d= =,则 z=d2=( )2= ,故 z 的取值范围是[ ,13], 故答案为:[ ,13]. 【点评】本题主要考查线性规划的应用,涉及距离的计算,利用数形结合是解决本题的关键 . 13.(5 分)(2016•江苏)如图,在△ABC 中,D 是 BC 的中点,E,F 是 AD 上的两个三 等分点, •=4, •=﹣1,则 •的值是 . 【分析】由已知可得 +2 =+,=﹣ +,=+3 ,=﹣ +3 ,22=,=﹣ +2 ,结合已知求出 =,=,可得答案. 【解答】解:∵D 是 BC 的中点,E,F 是 AD 上的两个三等分点, ∴=+,=﹣ +,,=+3 ,=﹣ +3 2∴•=﹣2=﹣1, 2•=9 ﹣2=4, 22∴=,=,又∵ ∴=+2 ,=﹣ +2 ,22•=4 ﹣= , 故答案为: 【点评】本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档. 14.(5 分)(2016•江苏)在锐角三角形 ABC 中,若 sinA=2sinBsinC,则 tanAtanBtanC 的 最小值是 8 . 【分析】结合三角形关系和式子 sinA=2sinBsinC 可推出 sinBcosC+cosBsinC=2sinBsinC,进 而得到 tanB+tanC=2tanBtanC,结合函数特性可求得最小值. 【解答】解:由 sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC, 可得 sinBcosC+cosBsinC=2sinBsinC,① 由三角形 ABC 为锐角三角形,则 cosB>0,cosC>0, 在①式两侧同时除以 cosBcosC 可得 tanB+tanC=2tanBtanC, 又 tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣ ②, 则 tanAtanBtanC=﹣ •tanBtanC, 由 tanB+tanC=2tanBtanC 可得 tanAtanBtanC=﹣ ,令 tanBtanC=t,由 A,B,C 为锐角可得 tanA>0,tanB>0,tanC>0, 由②式得 1﹣tanBtanC<0,解得 t>1, tanAtanBtanC=﹣ =﹣ ,=( )2﹣ ,由 t>1 得,﹣ ≤<0, 因此 tanAtanBtanC 的最小值为 8, 当且仅当 t=2 时取到等号,此时 tanB+tanC=4,tanBtanC=2, 解得 tanB=2+ ,tanC=2﹣ ,tanA=4,(或 tanB,tanC 互换),此时 A,B,C 均为锐 角. 【点评】本题考查了三角恒等式的变化技巧和函数单调性知识,有一定灵活性. 二、解答题(共 6 小题,满分 90 分) 15.(14 分)(2016•江苏)在△ABC 中,AC=6,cosB= ,C= (1)求 AB 的长; .(2)求 cos(A﹣ )的值. 【分析】(1)利用正弦定理,即可求 AB 的长; (2)求出 cosA、sinA,利用两角差的余弦公式求 cos(A﹣ )的值. 【解答】解:(1)∵△ABC 中,cosB= ,∴sinB= ,∵,∴AB= =5 ;(2)cosA=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣ ∵A 为三角形的内角, .∴sinA= ,∴cos(A﹣ )= cosA+ sinA= .【点评】本题考查正弦定理,考查两角和差的余弦公式,考查学生的计算能力,属于基础题 . 16.(14 分)(2016•江苏)如图,在直三棱柱 ABC﹣A1B1C1 中,D,E 分别为 AB,BC 的中点,点 F 在侧棱 B1B 上,且 B1D⊥A1F,A1C1⊥A1B1.求证: (1)直线 DE∥平面 A1C1F; (2)平面 B1DE⊥平面 A1C1F. 【分析】(1)通过证明 DE∥AC,进而 DE∥A1C1,据此可得直线 DE∥平面 A1C1F1; (2)通过证明 A1F⊥DE 结合题目已知条件 A1F⊥B1D,进而可得平面 B1DE⊥平面 A1C1F. 【解答】解:(1)∵D,E 分别为 AB,BC 的中点, ∴DE 为△ABC 的中位线, ∴DE∥AC, ∵ABC﹣A1B1C1 为棱柱, ∴AC∥A1C1, ∴DE∥A1C1, ∵A1C1⊂平面 A1C1F,且 DE⊄平面 A1C1F, ∴DE∥A1C1F; (2)∵ABC﹣A1B1C1 为直棱柱, ∴AA1⊥平面 A1B1C1, ∴AA1⊥A1C1, 又∵A1C1⊥A1B1,且 AA1∩A1B1=A1,AA1、A1B1⊂平面 AA1B1B, ∴A1C1⊥平面 AA1B1B, ∵DE∥A1C1, ∴DE⊥平面 AA1B1B, 又∵A1F⊂平面 AA1B1B, ∴DE⊥A1F, 又∵A1F⊥B1D,DE∩B1D=D,且 DE、B1D⊂平面 B1DE, ∴A1F⊥平面 B1DE, 又∵A1F⊂平面 A1C1F, ∴平面 B1DE⊥平面 A1C1F. 【点评】本题考查直线与平面平行的证明,以及平面与平面相互垂直的证明,把握常用方法 最关键,难度不大. 17.(14 分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正 四棱锥 P﹣A1B1C1D1,下部的形状是正四棱柱 ABCD﹣A1B1C1D1(如图所示),并要求正 四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. (1)若 AB=6m,PO1=2m,则仓库的容积是多少? (2)若正四棱锥的侧棱长为 6m,则当 PO1 为多少时,仓库的容积最大? 【分析】(1)由正四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍,可得 PO1=2m 时,O1O=8m ,进而可得仓库的容积; (2)设 PO1=xm,则 O1O=4xm,A1O1= m,A1B1= •m,代入体积公 式,求出容积的表达式,利用导数法,可得最大值. 【解答】解:(1)∵PO1=2m,正四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. ∴O1O=8m, ∴仓库的容积 V= ×62×2+62×8=312m3, (2)若正四棱锥的侧棱长为 6m, 设 PO1=xm, 则 O1O=4xm,A1O1= m,A1B1= •m, 22则仓库的容积 V= ×( x<6), •)•x+( •)•4x= x3+312x,(0< ∴V′=﹣26×2+312,(0<x<6), 当 0<x<2 时,V′>0,V(x)单调递增; 当 2 <x<6 时,V′<0,V(x)单调递减; 故当 x=2 时,V(x)取最大值; 即当 PO1=2 m时,仓库的容积最大. 【点评】本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档. 18.(16 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知以 M 为圆心的圆 M: x2+y2﹣12x﹣14y+60=0 及其上一点 A(2,4). (1)设圆 N 与 x 轴相切,与圆 M 外切,且圆心 N 在直线 x=6 上,求圆 N 的标准方程; (2)设平行于 OA 的直线 l 与圆 M 相交于 B、C 两点,且 BC=OA,求直线 l 的方程; (3)设点 T(t,0)满足:存在圆 M 上的两点 P 和 Q,使得 +=,求实数 t 的取值 范围. 【分析】(1)设 N(6,n),则圆 N 为:(x﹣6)2+(y﹣n)2=n2,n>0,从而得到 |7﹣n|=|n|+5,由此能求出圆 N 的标准方程. (2)由题意得 OA=2 ,kOA=2,设 l:y=2x+b,则圆心 M 到直线 l 的距离:d= 由此能求出直线 l 的方程. ,(3) =,即| |= ,2+2 ,又| |≤10,得 t∈[2﹣2 ,2+2 ], 对于任意 t∈[2﹣2 ],欲使 ,只需要作直线 TA 的平行线,使圆心到直 线的距离为 ,由此能求出实数 t 的取值范围. 【解答】解:(1)∵N 在直线 x=6 上,∴设 N(6,n), ∵圆 N 与 x 轴相切,∴圆 N 为:(x﹣6)2+(y﹣n)2=n2,n>0, 22又圆 N 与圆 M 外切,圆 M:x2+y2﹣12x﹣14y+60=0,即圆 M:((x﹣6)+(x﹣7)=25, ∴|7﹣n|=|n|+5,解得 n=1, ∴圆 N 的标准方程为(x﹣6)2+(y﹣1)2=1. (2)由题意得 OA=2 ,kOA=2,设 l:y=2x+b, 则圆心 M 到直线 l 的距离:d= =,则|BC|=2 =2 ,BC=2 ,即 2 =2 ,解得 b=5 或 b=﹣15, ∴直线 l 的方程为:y=2x+5 或 y=2x﹣15. (3) |= =,即 ,即| |=| |, |,又| |≤10,即 对于任意 t∈[2﹣2 ≤10,解得 t∈[2﹣2 ,2+2 ], ,2+2 ],欲使 ,此时,| |≤10, 只需要作直线 TA 的平行线,使圆心到直线的距离为 ,必然与圆交于 P、Q 两点,此时| |=| |,即 ,因此实数 t 的取值范围为 t∈[2﹣2 ,2+2 ],. 【点评】本题考查圆的标准方程的求法,考查直线方程的求法,考查实数的取值范围的求法 ,是中档题,解题时要认真审题,注意圆的性质的合理运用. 19.(16 分)(2016•江苏)已知函数 f(x)=ax+bx(a>0,b>0,a≠1,b≠1). (1)设 a=2,b= .①求方程 f(x)=2 的根; ②若对于任意 x∈R,不等式 f(2x)≥mf(x)﹣6 恒成立,求实数 m 的最大值; (2)若 0<a<1,b>1,函数 g(x)=f(x)﹣2 有且只有 1 个零点,求 ab 的值. 【分析】(1)①利用方程,直接求解即可.②列出不等式,利用二次函数的性质以及函 数的最值,转化求解即可. (2)求出 g(x)=f(x)﹣2=ax+bx﹣2,求出函数的导数,构造函数 h(x)= +,求出 g(x)的最小值为:g(x0).同理①若 g(x0)<0,g(x)至少有两个零点,与条 件矛盾.②若 g(x0)>0,利用函数 g(x)=f(x)﹣2 有且只有 1 个零点,推出 g(x0)=0 ,然后求解 ab=1. 【解答】解:函数 f(x)=ax+bx(a>0,b>0,a≠1,b≠1). (1)设 a=2,b= .①方程 f(x)=2;即: ②不等式 f(2x)≥mf(x)﹣6 恒成立,即 令 t= ,t≥2. =2,可得 x=0. ≥m( )﹣6 恒成立. 不等式化为:t2﹣mt+4≥0 在 t≥2 时,恒成立.可得:△≤0 或 即:m2﹣16≤0 或 m≤4, ∴m∈(﹣∞,4]. 实数 m 的最大值为:4. (2)g(x)=f(x)﹣2=ax+bx﹣2, g′(x)=axlna+bxlnb=ax[ +]lnb, 0<a<1,b>1 可得 ,令 h(x)= 因此,x0= +,则 h(x)是递增函数,而,lna<0,lnb>0, 时,h(x0)=0, 因此 x∈(﹣∞,x0)时,h(x)<0,axlnb>0,则 g′(x)<0. x∈(x0,+∞)时,h(x)>0,axlnb>0,则 g′(x)>0, 则 g(x)在(﹣∞,x0)递减,(x0,+∞)递增,因此 g(x)的最小值为:g(x0). ①若 g(x0)<0,x<loga2 时,ax> =2,bx>0,则 g(x)>0, 因此 x1<loga2,且 x1<x0 时,g(x1)>0,因此 g(x)在(x1,x0)有零点, 则 g(x)至少有两个零点,与条件矛盾. ②若 g(x0)>0,函数 g(x)=f(x)﹣2 有且只有 1 个零点,g(x)的最小值为 g(x0), 可得 g(x0)=0, 由 g(0)=a0+b0﹣2=0, 因此 x0=0,因此 =0,﹣ =1,即 lna+lnb=0,ln(ab)=0,则 ab=1. 可得 ab=1. 【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒 成立的应用,考查分析问题解决问题的能力. 20.(16 分)(2016•江苏)记 U={1,2,…,100},对数列{an}(n∈N*)和 U 的子集 T, 若 T=∅,定义 ST=0;若 T={t1,t2,…,tk},定义 ST= ++…+ .例如:T={1,3, 66}时,ST=a1+a3+a66.现设{an}(n∈N*)是公比为 3 的等比数列,且当 T={2,4}时,ST=30 .(1)求数列{an}的通项公式; (2)对任意正整数 k(1≤k≤100),若 T⊆{1,2,…,k},求证:ST<ak+1 (3)设 C⊆U,D⊆U,SC≥SD,求证:SC+SC∩D≥2SD. ;【分析】(1)根据题意,由 ST 的定义,分析可得 ST=a2+a4=a2+9a2=30,计算可得 a2=3,进 而可得 a1 的值,由等比数列通项公式即可得答案; (2)根据题意,由 ST 的定义,分析可得 ST≤a1+a2+…ak=1+3+32+…+3k﹣1,由等比数列的前 n 项和公式计算可得证明; (3)设 A=∁C(C∩D),B=∁D(C∩D),则 A∩B=∅,进而分析可以将原命题转化为证明 SC ≥2SB,分 2 种情况进行讨论:①、若 B=∅,②、若 B≠∅,可以证明得到 SA≥2SB,即可 得证明. 【解答】解:(1)当 T={2,4}时,ST=a2+a4=a2+9a2=30, 因此 a2=3,从而 a1= 故 an=3n﹣1 =1, ,(2)ST≤a1+a2+…ak=1+3+32+…+3k﹣1 =<3k=ak+1 ,(3)设 A=∁C(C∩D),B=∁D(C∩D),则 A∩B=∅, 分析可得 SC=SA+SC∩D,SD=SB+SC∩D,则 SC+SC∩D﹣2SD=SA﹣2SB, 因此原命题的等价于证明 SC≥2SB, 由条件 SC≥SD,可得 SA≥SB, ①、若 B=∅,则 SB=0,故 SA≥2SB, ②、若 B≠∅,由 SA≥SB 可得 A≠∅,设 A 中最大元素为 l,B 中最大元素为 m, 若 m≥l+1,则其与 SA<ai+1≤am≤SB 相矛盾, 因为 A∩B=∅,所以 l≠m,则 l≥m+1, SB≤a1+a2+…am=1+3+32+…+3m﹣1 =≤=,即 SA≥2SB, 综上所述,SA≥2SB, 故 SC+SC∩D≥2SD. 【点评】本题考查数列的应用,涉及新定义的内容,解题的关键是正确理解题目中对于新定 义的描述. 附加题【选做题】本题包括 A、B、C、D 四小题,请选定其中两小题,并在相应的答题区 域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算 步骤.A.【选修 4—1 几何证明选讲】 21.(10 分)(2016•江苏)如图,在△ABC 中,∠ABC=90°,BD⊥AC,D 为垂足,E 为 BC 的中点,求证:∠EDC=∠ABD. 【分析】依题意,知∠BDC=90°,∠EDC=∠C,利用∠C+∠DBC=∠ABD+∠DBC=90°,可 得∠ABD=∠C,从而可证得结论. 【解答】解:由 BD⊥AC 可得∠BDC=90°, 因为 E 为 BC 的中点,所以 DE=CE= BC, 则:∠EDC=∠C, 由∠BDC=90°,可得∠C+∠DBC=90°, 由∠ABC=90°,可得∠ABD+∠DBC=90°, 因此∠ABD=∠C,而∠EDC=∠C, 所以,∠EDC=∠ABD. 【点评】本题考查三角形的性质应用,利用∠C+∠DBC=∠ABD+∠DBC=90°,证得∠ABD= ∠C 是关键,属于中档题. B.【选修 4—2:矩阵与变换】 22.(10 分)(2016•江苏)已知矩阵 A= 矩阵 AB. ,矩阵 B 的逆矩阵 B﹣1 =,求 ﹣1 【分析】依题意,利用矩阵变换求得 B=(B﹣1 )==,再利用矩阵乘法的性 质可求得答案. 【解答】解:∵B﹣1 =,﹣1 ∴B=(B﹣1 )==,又 A= ,∴AB= =.【点评】本题考查逆变换与逆矩阵,考查矩阵乘法的性质,属于中档题. C.【选修 4—4:坐标系与参数方程】 23.(2016•江苏)在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参 数),椭圆 C 的参数方程为 点,求线段 AB 的长. (θ 为参数),设直线 l 与椭圆 C 相交于 A,B 两 【分析】分别化直线与椭圆的参数方程为普通方程,然后联立方程组,求出直线与椭圆的交 点坐标,代入两点间的距离公式求得答案. 【解答】解:由 ,由②得 ,代入①并整理得, .由,得 ,两式平方相加得 .联立 ,解得 或.∴|AB|= .【点评】本题考查直线与椭圆的参数方程,考查了参数方程化普通方程,考查直线与椭圆位 置关系的应用,是基础题. 24.(2016•江苏)设 a>0,|x﹣1|< ,|y﹣2|< ,求证:|2x+y﹣4|<a. 【分析】运用绝对值不等式的性质:|a+b|≤|a|+|b|,结合不等式的基本性质,即可得证. 【解答】证明:由 a>0,|x﹣1|< ,|y﹣2|< 可得|2x+y﹣4|=|2(x﹣1)+(y﹣2)| ,≤2|x﹣1|+|y﹣2|< + =a, 则|2x+y﹣4|<a 成立. 【点评】本题考查绝对值不等式的证明,注意运用绝对值不等式的性质,以及不等式的简单 性质,考查运算能力,属于基础题. 附加题【必做题】 25.(10 分)(2016•江苏)如图,在平面直角坐标系 xOy 中,已知直线 l:x﹣y﹣2=0, 抛物线 C:y2=2px(p>0). (1)若直线 l 过抛物线 C 的焦点,求抛物线 C 的方程; (2)已知抛物线 C 上存在关于直线 l 对称的相异两点 P 和 Q. ①求证:线段 PQ 的中点坐标为(2﹣p,﹣p); ②求 p 的取值范围. 【分析】(1)求出抛物线的焦点坐标,然后求解抛物线方程. (2):①设点 P(x1,y1),Q(x2,y2),通过抛物线方程,求解 kPQ,通过 P,Q 关于 直线 l 对称,点的 kPQ=﹣1,推出 ,PQ 的中点在直线 l 上,推出 =2﹣p ,即可证明线段 PQ 的中点坐标为(2﹣p,﹣p); ②利用线段 PQ 中点坐标(2﹣p,﹣p).推出 ,得到关于 y2+2py+4p2﹣4p=0,有两个不相等的实数根,列出不等式即可求出 p 的范围. 【解答】解:(1)∵l:x﹣y﹣2=0,∴l 与 x 轴的交点坐标(2,0), 即抛物线的焦点坐标(2,0). ∴,∴抛物线 C:y2=8x. (2)证明:①设点 P(x1,y1),Q(x2,y2),则: ,即: ,kPQ ==,又∵P,Q 关于直线 l 对称,∴kPQ=﹣1,即 y1+y2=﹣2p,∴ ,又 PQ 的中点在直线 l 上,∴ ==2﹣p, ∴线段 PQ 的中点坐标为(2﹣p,﹣p); ②因为 Q 中点坐标(2﹣p,﹣p). ∴∴,即 ,即关于 y2+2py+4p2﹣4p=0,有两个不相等的实数根, ∴△>0,(2p)2﹣4(4p2﹣4p)>0, ∴p∈ .【点评】本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及 计算能力. 26.(10 分)(2016•江苏)(1)求 7C ﹣4C 的值; (2)设 m,n∈N*,n≥m,求证:(m+1)C +(m+2)C +…+nC +(n+1)C =(m+1)C 【分析】(1)由已知直接利用组合公式能求出 7 (2)对任意 m∈N*,当 n=m 时,验证等式成立;再假设 n=k(k≥m)时命题成立,推导出 +(m+3) C.的值. 当 n=k+1 时,命题也成立,由此利用数学归纳法能证明(m+1)C +(m+2)C )C +…+nC +(n+1)C =(m+1)C 【解答】解:(1)7 ﹣4× =7×20﹣4×35=0. +(m+3 .=证明:(2)对任意 m∈N*, ①当 n=m 时,左边=(m+1) =m+1, 右边=(m+1) =m+1,等式成立. ②假设 n=k(k≥m)时命题成立, 即(m+1)C +(m+2)C +(m+3)C +…+k +(k+1) =(m+1) +(k+1) +(k+2) ,当 n=k+1 时, 左边=(m+1) +(m+2) +(m+3) +=,右边= ∵=(m+1)[ =(m+1)× =(k+2) =(k+2) ∴﹣][k+3﹣(k﹣m+1)] ,=(m+1) ,∴左边=右边, ∴n=k+1 时,命题也成立, ∴m,n∈N*,n≥m,(m+1)C +(m+2)C +(m+3)C +…+nC +(n+1)C =(m+1)C .【点评】本题考查组合数的计算与证明,是中档题,解题时要认真审题,注意组合数公式和 数学归纳法的合理运用.
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





