
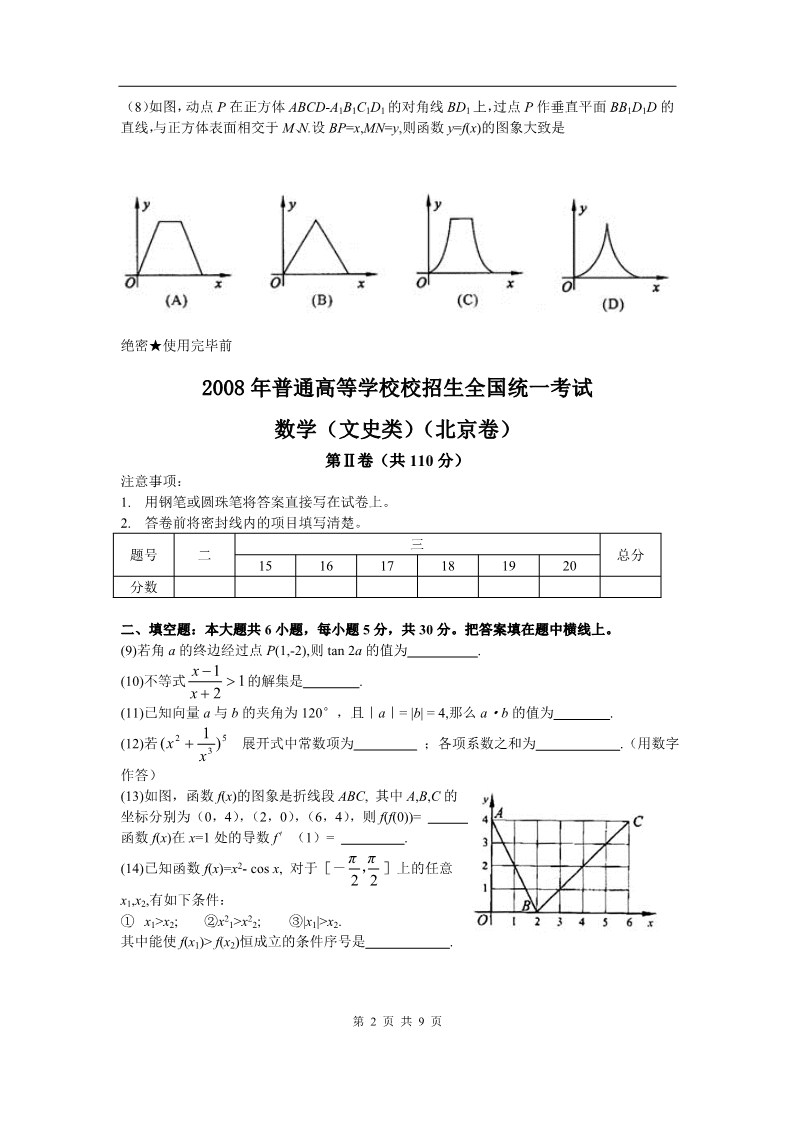
 绝密★启用前 2008年普通高等学校招生全国统一考试(北京卷) 数学(文史类) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷 1 至 2 页。第Ⅱ卷 3 至 9 页,共 150 分,考试时间 120 分钟。考试结束,将本试卷和答题卡一并交回。 第Ⅰ卷(选择题 共 40 分) 注意事项: 1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。 2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡颇擦 干净后,再选涂其他答案。不能答在试卷上。 一、本大题共 8 小题,第小题 5 分,共 40 分。在每小题列出的四个选项中,选出符合题目 要求的一项。 (1)若集合 A={x|-2≤x≤3}≤3, B={x|x<-1 或 x>4}, 则集合 A∩B 等于 (A){x|x≤3 或 x>4} (C){x|3≤x<4} (B){x|-1<x≤3} (D) {x|-2≤x<-1} (2)若 a=log3π, b=log76,c=log20.8, 则 (A)a>b>c (B)b>a>c (D)b>c>a (C)c>a>b x2 y2 9(3)“双曲线的方程为 1”是“双曲线的准线方程为 x= ”的 916 5(A)充分而不必要条件 (C)充分必要条件 (B)必要而不充分条件 (D)既不充分也不必要条件 (4)已知△ABC 中,a= 2,b= 3,B=60°,那么角 A 等于 (C)45° (A)135° (B)90° (D)30° (5)函数 f(x)=(x-1)2+1(x<1)的反函数为 (A)f –1(x)=1+ x 1 (x>1) (B)f–1(x)=1- x 1 (x>1) (D)f–1(x)=1- x 1 (x≥1) (C)f –1(x)=1+ x 1 (x≥1) x-y+1≥0, (6)若实数 x,y 满足 x+y≥0, 则 z=x+2y 的最小值是 x≤0, 1(A)0 (D)2 (B) (C) 12(7)已知等差数列{an}中,a2=6,a5=15.若 bn=a2n,则数列{bn} 的前 5 项和等于 (A)30 (C)90 (B)45 (D)186 第 1 页 共 9 页 (8)如图,动点 P 在正方体 ABCD-A1B1C1D1 的对角线 BD1 上,过点 P 作垂直平面 BB1D1D 的 直线,与正方体表面相交于 M、N.设 BP=x,MN=y,则函数 y=f(x)的图象大致是 绝密★使用完毕前 2008年普通高等学校校招生全国统一考试 数学(文史类)(北京卷) 第Ⅱ卷(共 110 分) 注意事项: 1. 用钢笔或圆珠笔将答案直接写在试卷上。 2. 答卷前将密封线内的项目填写清楚。 三 题号 二总分 15 16 17 18 19 20 分数 二、填空题:本大题共 6 小题,每小题 5 分,共 30 分。把答案填在题中横线上。 (9)若角 a 的终边经过点 P(1,-2),则 tan 2a 的值为 . x 1 (10)不等式 1的解集是 . x 2 (11)已知向量 a 与 b 的夹角为 120°,且|a|= |b| = 4,那么 a·b 的值为 . 1×3 5(12)若 (x2 )展开式中常数项为 ;各项系数之和为 .(用数字 作答) (13)如图,函数 f(x)的图象是折线段 ABC, 其中 A,B,C 的 坐标分别为(0,4),(2,0),(6,4),则 f(f(0))= ;函数 f(x)在 x=1 处的导数 f′(1)= (14)已知函数 f(x)=x2- cos x, 对于[- x1,x2,有如下条件: .π π ,]上的任意 2 2 ① x1>x2; ②x2 >x2 ; ③|x1|>x2. 12其中能使 f(x1)> f(x2)恒成立的条件序号是 . 第 2 页 共 9 页 三、解答题:本大题共 6小题,共 80分。解答应写出文字说明。演算步骤或证明过程。 (15)(本小题共 13 分) 已知函数 f (x) sin2 x 3sinxsin(x )( 0) 的最小正周期为π. 2(Ⅰ)求ω的值; 2 3(Ⅱ)求函数 f(x)在区间[0, ]上的取值范围. (16)(本小题共 14 分) 如图,在三棱锥 P-ABC 中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. (Ⅰ)求证:PC⊥AB; (Ⅱ)求二面角 B-AP-C 的大小. (17)(本小题共 13 分) 已知函数 f (x) x3 ax2 3bx c(b 0),且g(x) f (x) 2 是奇函数. (Ⅰ)求 a,c 的值; (Ⅱ)求函数 f(x)的单调区间. (18)(本小题共 13 分) 甲、乙等五名奥运志愿者被随机地分到 A,B,C,D 四个不同的岗位服务,每个岗位 至少有一名志愿者. (Ⅰ)求甲、乙两人同时参加 A 岗位服务的概率; (Ⅱ)求甲、乙两人不在同一个岗位服务的概率。 第 3 页 共 9 页 (19)(本小题共 14 分) 已知△ABC 的顶点 A,B 在椭圆 x2 3y2 4上,C 在直线 l: y=x+2 上,且 AB∥l. (Ⅰ)当 AB 边通过坐标原点 O 时,求 AB 的长及△ABC 的面积; (Ⅱ)当∠ABC=90°,且斜边 AC 的长最大时,求 AB 所在直线的方程. (20)(本小题共 13 分) 数列{an}满足 a1 1,an1 (n2 n )an (n 1,2,……),是常数. (Ⅰ)当 a2=-1 时,求λ及 a3 的值; (Ⅱ)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由; (Ⅲ)求λ的取值范围,使得存在正整数 m, 当 n>m 时总有 an<0. 第 4 页 共 9 页 绝密★考试结束前 2008年普通高等学校招生全国统一考试 数学(文史类)(北京卷)参考答案 一、选择题(本大题共 8 小题,每小题 5 分,共 40 分) (1)D (5)B (2)A (6)A (3)A (7)C (4)C (8)B 二、填空题(本大题共 6 小题,每小题 5 分,共 30 分) 4(9) (10)|x|x<-2| 3(11)-8 (12)10 (14)② 32 (13)2 -2 三、解答题(本大题共 6 小题,共 80 分) (15)(共 13 分) 1 cos2x 3解:(Ⅰ) f (x) sin 2x 223112==sinx cos2x 221sin(2x ) . 62因为函数 f(x)的最小正周期为π,且ω>0, 2 2 所以 解得ω=1. 61(Ⅱ)由(Ⅰ)得 f (x) sin(2x ) . 22 3因为 0≤x≤ ,6167 6所以 所以 ≤2x ≤.6≤sin (2x )≤1. 26123232因此 0≤sin(2x ) ≤,即 f(x)的取值范围为[0, ](16)(共 14 分) 解法一: (Ⅰ)取 AB 中点 D,连结 PD,CD. ∵AP=BP, ∴PD⊥AB. 第 5 页 共 9 页 ∵AC=BC. ∴CD⊥AB. ∵PD∩CD=D. ∴AB⊥平面 PCD. ∵PC 平面 PCD, ∴PC⊥AB. (Ⅱ)∵AC=BC, AP=BP, ∴△APC≌△BPC. 又 PC⊥AC, ∴PC⊥BC. 又∠ACB=90°,即 AC⊥BC, 且 AC∩PC=C, ∴BC⊥平面 PAC 取 AP 中点 E,连接 BE,CE ∵AB=BP ∴BE⊥AP. ∵EC 是 BE 在平面 PAC 内的射影, ∴CE⊥AP. ∴∠BEC 是二面角 B-AP-C 的平面角. 3在△BCE 中,∠BCE=90°, BC=2, BE= AB 6 ,2BC BE 6∴sin∠BEC= .36∴二面角 B-AP-C 的大小为 aresin .3解法二: (Ⅰ)∵AC=BC, AP=BP, ∴△APC≌△BPC. 又 PC⊥AC. ∴PC⊥BC. ∵AC∩BC=C, ∴PC⊥平面 ABC. ∵AB 平面 ABC, ∴PC⊥AB. (Ⅱ)如图,以 C 为原点建立空间直角坐标系 C-xyz. 则 C(0,0,0),A(0,2,0),B(2,0,0). 设 P(0,0,t), ∵|PB|=|AB|=2 2 , 第 6 页 共 9 页 ∴t=2, P(0,0,2). 取 AP 中点 E,连结 BE,CE. ∵|AC|=|PC|,|AB|=|BP|, ∴CE⊥AP, BE⊥AP. ∴∠BEC 是二面角 B-AP-C 的平面角. ∵E(0,1,1), EC (0,1,1), EB (2,1,1), EC EB EC EB 23.∴cos∠BEC= 32 6 3∴二面角 B-AP-C 的大小为 arccos (17)(共 13 分) .3解:(Ⅰ)因为函数 g(x)=f(x)-2 为奇函数, 所以,对任意的 x∈R, g (-x)= -g (x), 即 f (-x)- 2= -f (x)+2. 又 f(x)=x3+ax2+3bx+c, 所以-x3+ax2-3bx+c-2=-x3-ax2-3bx-c+2. a a, 所以 {c 2 c 2. 解得 a=0,c=2. (Ⅱ)由(Ⅰ)得 f(x)=x3+3bx+2. 所以 f′(x)=3×2+3b(b≠0). 当 b<0 时,由 f′(x)=0 得 x=± b. x 变化时,f′(x)的变化情况如下表: x(-∞,- b )- b (- b , b ) b ( b ,+∞) f′(x) +0-0+所以,当 b<0 时,函数 f (x)在(-∞,- b )上单调递增,在(- b , b )上单调 递减,在( b ,+∞)上单调递增. 当 b>0 时,f′(x)>0.所以函数 f (x)在(-∞,+∞)上单调递增. (18)(共 13 分) 解: (Ⅰ)记甲、乙两人同时参加 A 岗位服务为事件 EA,那么 A33 C32 A44 1 P(EA)= .40 第 7 页 共 9 页 1即甲、乙两人同时参加 A 岗位服务的概率是 .40 (Ⅱ)记甲、乙两个同时参加同一岗位服务为事件 E,那么 A44 C32 A44 1P(E)= .10 所以,甲、乙两人不在同一岗位服务的概率是 9P( E)=1-P(E)= .10 (19)(共 14 分) 解:(Ⅰ)因为 AB∥l,且 AB 边通过点(0,0),所以 AB 所在直线的方程为 y=x. 设 A,B 两点坐标分别为(x1,y1),(x2,y2). 22x 3y 4, y x 由得x 1, 所以 AB 2 x1 x2 2 2. 又因为 AB 边上的高 h 等于原点到直线 l 的距离, 1所以 h 2.SABC AB h 2. 2(Ⅱ)设 AB 所在直线的方程为 y=x+m. 22x 3y 4, y x m 由得4×2 6mx 3m2 4 0. 因为 A,B 在椭圆上, 所以 12m2 64>0. 设A,B 两点坐标分别为(x1, y1),(x2, y2). 3m 3m2 4 则x1 x2 , x1x2 ,2432 6m2 所以 AB 2 x1 x2 .22 m 又因为BC 的长等于点(0, m)到直线 l 的距离,即 BC .2所以 AC 2 AB 2 BC 2 m2 2m 10 (m 1)2 11. 所以当m=-1 时,AC 边最长.(这时 12 64>0 此时 AB 所在直线的方程为 y=x-1. (20)(共 13 分) )解:(Ⅰ)由于 an1 (n2 n )an (n 1,2,), 且 a1=1, 第 8 页 共 9 页 所以当 a2= -1 时,得 1 2 3. ,故 从而 a3 (22 2 3)(1) 3. (Ⅱ)数列{an}不可能为等差数列.证明如下: 由 a1=1, an1 (n2 n )an 得 a2 2 ,a3 (6 )(2 ),a4 (12 )(6 )(2 ). 若存在 ,使{an}为等差数列,则 a3-a2=a2-a1,即 (5 )(2 ) 1 , 解得 =3. 于是 a2 a1 1 2,a4 a3 (11 )(6 )(2 ) 24. 这与{an}为等差数列矛盾,所以,对任意 ,{an}都不可能是等差数列. ( Ⅲ ) 记 bn n2 n (n 1,2,), 根 据 题 意 可 知 , b1 < 0 且 bn 0 , 即 > 2 且 n2 n(nN*),这时总存在 n0 N*,满足:当 n≥n0 时,bn>0;当 n≤n0-1 时,bn<0. 所以由 an+1=bnan 及 a1=1>0 可知,若 n0 为偶数,则 an <0 ,从而当 n>n0 0时 an<0;若 n0 为奇数,则 an >0 ,从而当 n>n0 时 an>0. 0因此“存在 m N*,当 n>m 时总有 an<0”的充分必要条件是:no 为偶数, 记 no=2k(k=1,2, …),则 满足 b2k (2k)2 2k >0, b2k1 (2k 1)2 2k 1 <0. 故的取值范围是 4k2 2k<<4k2+2k (k N*). 第 9 页 共 9 页
绝密★启用前 2008年普通高等学校招生全国统一考试(北京卷) 数学(文史类) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷 1 至 2 页。第Ⅱ卷 3 至 9 页,共 150 分,考试时间 120 分钟。考试结束,将本试卷和答题卡一并交回。 第Ⅰ卷(选择题 共 40 分) 注意事项: 1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。 2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡颇擦 干净后,再选涂其他答案。不能答在试卷上。 一、本大题共 8 小题,第小题 5 分,共 40 分。在每小题列出的四个选项中,选出符合题目 要求的一项。 (1)若集合 A={x|-2≤x≤3}≤3, B={x|x<-1 或 x>4}, 则集合 A∩B 等于 (A){x|x≤3 或 x>4} (C){x|3≤x<4} (B){x|-1<x≤3} (D) {x|-2≤x<-1} (2)若 a=log3π, b=log76,c=log20.8, 则 (A)a>b>c (B)b>a>c (D)b>c>a (C)c>a>b x2 y2 9(3)“双曲线的方程为 1”是“双曲线的准线方程为 x= ”的 916 5(A)充分而不必要条件 (C)充分必要条件 (B)必要而不充分条件 (D)既不充分也不必要条件 (4)已知△ABC 中,a= 2,b= 3,B=60°,那么角 A 等于 (C)45° (A)135° (B)90° (D)30° (5)函数 f(x)=(x-1)2+1(x<1)的反函数为 (A)f –1(x)=1+ x 1 (x>1) (B)f–1(x)=1- x 1 (x>1) (D)f–1(x)=1- x 1 (x≥1) (C)f –1(x)=1+ x 1 (x≥1) x-y+1≥0, (6)若实数 x,y 满足 x+y≥0, 则 z=x+2y 的最小值是 x≤0, 1(A)0 (D)2 (B) (C) 12(7)已知等差数列{an}中,a2=6,a5=15.若 bn=a2n,则数列{bn} 的前 5 项和等于 (A)30 (C)90 (B)45 (D)186 第 1 页 共 9 页 (8)如图,动点 P 在正方体 ABCD-A1B1C1D1 的对角线 BD1 上,过点 P 作垂直平面 BB1D1D 的 直线,与正方体表面相交于 M、N.设 BP=x,MN=y,则函数 y=f(x)的图象大致是 绝密★使用完毕前 2008年普通高等学校校招生全国统一考试 数学(文史类)(北京卷) 第Ⅱ卷(共 110 分) 注意事项: 1. 用钢笔或圆珠笔将答案直接写在试卷上。 2. 答卷前将密封线内的项目填写清楚。 三 题号 二总分 15 16 17 18 19 20 分数 二、填空题:本大题共 6 小题,每小题 5 分,共 30 分。把答案填在题中横线上。 (9)若角 a 的终边经过点 P(1,-2),则 tan 2a 的值为 . x 1 (10)不等式 1的解集是 . x 2 (11)已知向量 a 与 b 的夹角为 120°,且|a|= |b| = 4,那么 a·b 的值为 . 1×3 5(12)若 (x2 )展开式中常数项为 ;各项系数之和为 .(用数字 作答) (13)如图,函数 f(x)的图象是折线段 ABC, 其中 A,B,C 的 坐标分别为(0,4),(2,0),(6,4),则 f(f(0))= ;函数 f(x)在 x=1 处的导数 f′(1)= (14)已知函数 f(x)=x2- cos x, 对于[- x1,x2,有如下条件: .π π ,]上的任意 2 2 ① x1>x2; ②x2 >x2 ; ③|x1|>x2. 12其中能使 f(x1)> f(x2)恒成立的条件序号是 . 第 2 页 共 9 页 三、解答题:本大题共 6小题,共 80分。解答应写出文字说明。演算步骤或证明过程。 (15)(本小题共 13 分) 已知函数 f (x) sin2 x 3sinxsin(x )( 0) 的最小正周期为π. 2(Ⅰ)求ω的值; 2 3(Ⅱ)求函数 f(x)在区间[0, ]上的取值范围. (16)(本小题共 14 分) 如图,在三棱锥 P-ABC 中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. (Ⅰ)求证:PC⊥AB; (Ⅱ)求二面角 B-AP-C 的大小. (17)(本小题共 13 分) 已知函数 f (x) x3 ax2 3bx c(b 0),且g(x) f (x) 2 是奇函数. (Ⅰ)求 a,c 的值; (Ⅱ)求函数 f(x)的单调区间. (18)(本小题共 13 分) 甲、乙等五名奥运志愿者被随机地分到 A,B,C,D 四个不同的岗位服务,每个岗位 至少有一名志愿者. (Ⅰ)求甲、乙两人同时参加 A 岗位服务的概率; (Ⅱ)求甲、乙两人不在同一个岗位服务的概率。 第 3 页 共 9 页 (19)(本小题共 14 分) 已知△ABC 的顶点 A,B 在椭圆 x2 3y2 4上,C 在直线 l: y=x+2 上,且 AB∥l. (Ⅰ)当 AB 边通过坐标原点 O 时,求 AB 的长及△ABC 的面积; (Ⅱ)当∠ABC=90°,且斜边 AC 的长最大时,求 AB 所在直线的方程. (20)(本小题共 13 分) 数列{an}满足 a1 1,an1 (n2 n )an (n 1,2,……),是常数. (Ⅰ)当 a2=-1 时,求λ及 a3 的值; (Ⅱ)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由; (Ⅲ)求λ的取值范围,使得存在正整数 m, 当 n>m 时总有 an<0. 第 4 页 共 9 页 绝密★考试结束前 2008年普通高等学校招生全国统一考试 数学(文史类)(北京卷)参考答案 一、选择题(本大题共 8 小题,每小题 5 分,共 40 分) (1)D (5)B (2)A (6)A (3)A (7)C (4)C (8)B 二、填空题(本大题共 6 小题,每小题 5 分,共 30 分) 4(9) (10)|x|x<-2| 3(11)-8 (12)10 (14)② 32 (13)2 -2 三、解答题(本大题共 6 小题,共 80 分) (15)(共 13 分) 1 cos2x 3解:(Ⅰ) f (x) sin 2x 223112==sinx cos2x 221sin(2x ) . 62因为函数 f(x)的最小正周期为π,且ω>0, 2 2 所以 解得ω=1. 61(Ⅱ)由(Ⅰ)得 f (x) sin(2x ) . 22 3因为 0≤x≤ ,6167 6所以 所以 ≤2x ≤.6≤sin (2x )≤1. 26123232因此 0≤sin(2x ) ≤,即 f(x)的取值范围为[0, ](16)(共 14 分) 解法一: (Ⅰ)取 AB 中点 D,连结 PD,CD. ∵AP=BP, ∴PD⊥AB. 第 5 页 共 9 页 ∵AC=BC. ∴CD⊥AB. ∵PD∩CD=D. ∴AB⊥平面 PCD. ∵PC 平面 PCD, ∴PC⊥AB. (Ⅱ)∵AC=BC, AP=BP, ∴△APC≌△BPC. 又 PC⊥AC, ∴PC⊥BC. 又∠ACB=90°,即 AC⊥BC, 且 AC∩PC=C, ∴BC⊥平面 PAC 取 AP 中点 E,连接 BE,CE ∵AB=BP ∴BE⊥AP. ∵EC 是 BE 在平面 PAC 内的射影, ∴CE⊥AP. ∴∠BEC 是二面角 B-AP-C 的平面角. 3在△BCE 中,∠BCE=90°, BC=2, BE= AB 6 ,2BC BE 6∴sin∠BEC= .36∴二面角 B-AP-C 的大小为 aresin .3解法二: (Ⅰ)∵AC=BC, AP=BP, ∴△APC≌△BPC. 又 PC⊥AC. ∴PC⊥BC. ∵AC∩BC=C, ∴PC⊥平面 ABC. ∵AB 平面 ABC, ∴PC⊥AB. (Ⅱ)如图,以 C 为原点建立空间直角坐标系 C-xyz. 则 C(0,0,0),A(0,2,0),B(2,0,0). 设 P(0,0,t), ∵|PB|=|AB|=2 2 , 第 6 页 共 9 页 ∴t=2, P(0,0,2). 取 AP 中点 E,连结 BE,CE. ∵|AC|=|PC|,|AB|=|BP|, ∴CE⊥AP, BE⊥AP. ∴∠BEC 是二面角 B-AP-C 的平面角. ∵E(0,1,1), EC (0,1,1), EB (2,1,1), EC EB EC EB 23.∴cos∠BEC= 32 6 3∴二面角 B-AP-C 的大小为 arccos (17)(共 13 分) .3解:(Ⅰ)因为函数 g(x)=f(x)-2 为奇函数, 所以,对任意的 x∈R, g (-x)= -g (x), 即 f (-x)- 2= -f (x)+2. 又 f(x)=x3+ax2+3bx+c, 所以-x3+ax2-3bx+c-2=-x3-ax2-3bx-c+2. a a, 所以 {c 2 c 2. 解得 a=0,c=2. (Ⅱ)由(Ⅰ)得 f(x)=x3+3bx+2. 所以 f′(x)=3×2+3b(b≠0). 当 b<0 时,由 f′(x)=0 得 x=± b. x 变化时,f′(x)的变化情况如下表: x(-∞,- b )- b (- b , b ) b ( b ,+∞) f′(x) +0-0+所以,当 b<0 时,函数 f (x)在(-∞,- b )上单调递增,在(- b , b )上单调 递减,在( b ,+∞)上单调递增. 当 b>0 时,f′(x)>0.所以函数 f (x)在(-∞,+∞)上单调递增. (18)(共 13 分) 解: (Ⅰ)记甲、乙两人同时参加 A 岗位服务为事件 EA,那么 A33 C32 A44 1 P(EA)= .40 第 7 页 共 9 页 1即甲、乙两人同时参加 A 岗位服务的概率是 .40 (Ⅱ)记甲、乙两个同时参加同一岗位服务为事件 E,那么 A44 C32 A44 1P(E)= .10 所以,甲、乙两人不在同一岗位服务的概率是 9P( E)=1-P(E)= .10 (19)(共 14 分) 解:(Ⅰ)因为 AB∥l,且 AB 边通过点(0,0),所以 AB 所在直线的方程为 y=x. 设 A,B 两点坐标分别为(x1,y1),(x2,y2). 22x 3y 4, y x 由得x 1, 所以 AB 2 x1 x2 2 2. 又因为 AB 边上的高 h 等于原点到直线 l 的距离, 1所以 h 2.SABC AB h 2. 2(Ⅱ)设 AB 所在直线的方程为 y=x+m. 22x 3y 4, y x m 由得4×2 6mx 3m2 4 0. 因为 A,B 在椭圆上, 所以 12m2 64>0. 设A,B 两点坐标分别为(x1, y1),(x2, y2). 3m 3m2 4 则x1 x2 , x1x2 ,2432 6m2 所以 AB 2 x1 x2 .22 m 又因为BC 的长等于点(0, m)到直线 l 的距离,即 BC .2所以 AC 2 AB 2 BC 2 m2 2m 10 (m 1)2 11. 所以当m=-1 时,AC 边最长.(这时 12 64>0 此时 AB 所在直线的方程为 y=x-1. (20)(共 13 分) )解:(Ⅰ)由于 an1 (n2 n )an (n 1,2,), 且 a1=1, 第 8 页 共 9 页 所以当 a2= -1 时,得 1 2 3. ,故 从而 a3 (22 2 3)(1) 3. (Ⅱ)数列{an}不可能为等差数列.证明如下: 由 a1=1, an1 (n2 n )an 得 a2 2 ,a3 (6 )(2 ),a4 (12 )(6 )(2 ). 若存在 ,使{an}为等差数列,则 a3-a2=a2-a1,即 (5 )(2 ) 1 , 解得 =3. 于是 a2 a1 1 2,a4 a3 (11 )(6 )(2 ) 24. 这与{an}为等差数列矛盾,所以,对任意 ,{an}都不可能是等差数列. ( Ⅲ ) 记 bn n2 n (n 1,2,), 根 据 题 意 可 知 , b1 < 0 且 bn 0 , 即 > 2 且 n2 n(nN*),这时总存在 n0 N*,满足:当 n≥n0 时,bn>0;当 n≤n0-1 时,bn<0. 所以由 an+1=bnan 及 a1=1>0 可知,若 n0 为偶数,则 an <0 ,从而当 n>n0 0时 an<0;若 n0 为奇数,则 an >0 ,从而当 n>n0 时 an>0. 0因此“存在 m N*,当 n>m 时总有 an<0”的充分必要条件是:no 为偶数, 记 no=2k(k=1,2, …),则 满足 b2k (2k)2 2k >0, b2k1 (2k 1)2 2k 1 <0. 故的取值范围是 4k2 2k<<4k2+2k (k N*). 第 9 页 共 9 页
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





