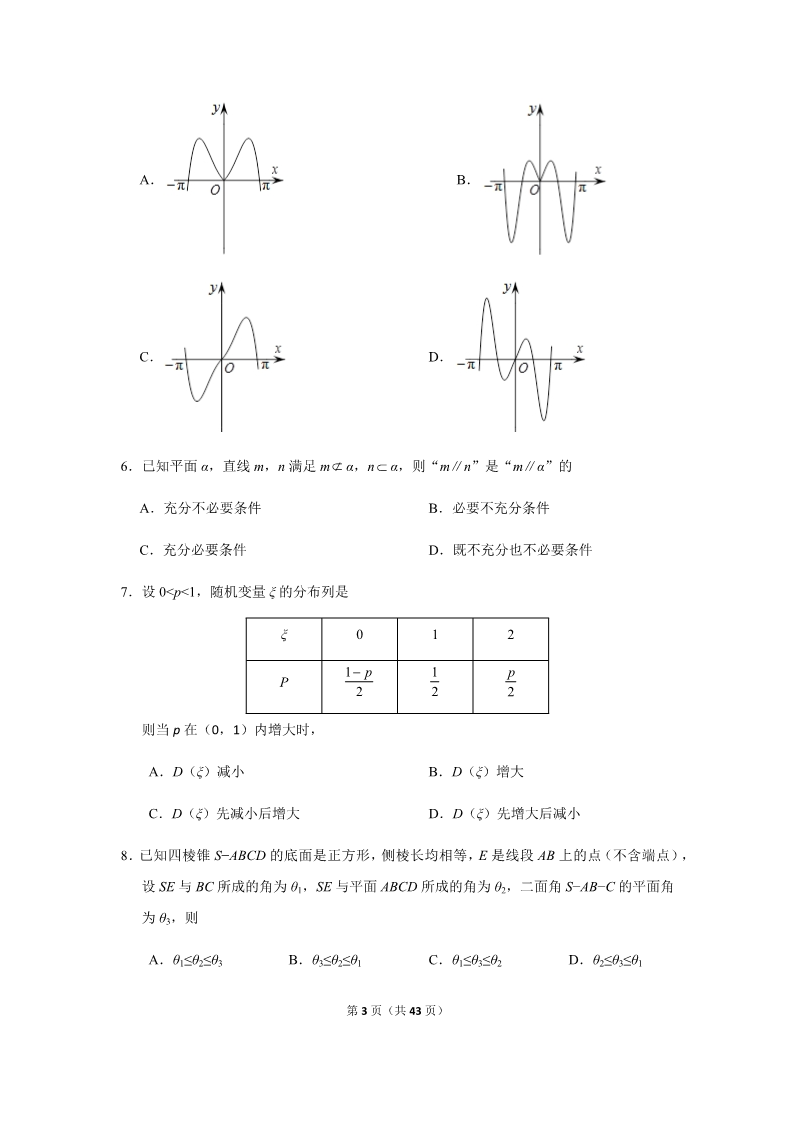
绝密★启用前 2018 年普通高等学校招生全国统一考试（浙江卷） 数 学 本试题卷分选择题和非选择题两部分。全卷共 4 页，选择题部分 1 至 2 页；非选择题部 分 3 至 4 页。满分 150 分。考试用时 120 分钟。 考生注意： 1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题 卷和答题纸规定的位置上。 2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答， 在本试题卷上的作答一律无效。 参考公式： V Sh 柱体的体积公式 若事件 A，B 互斥，则 P(A B) P(A) P(B) 若事件 A，B 相互独立，则 P(AB) P(A)P(B) Sh其中 表示柱体的底面积， 表示柱体的高 1V Sh 锥体的体积公式 3若事件 A 在一次试验中发生的概率是 p，则 n 次 独立重复试验中事件 A 恰好发生 k 次的概率 Sh其中 表示锥体的底面积， 表示锥体的高 P (k) Ckn pk (1 p)nk (k 0,1,2,,n) n球的表面积公式 S 4R2 1V (S1 S1S2 S2 )h 台体的体积公式 3球的体积公式 S ,S h2 分别表示台体的上、下底面积， 表 其中 14V R3 示台体的高 3其中 R 表示球的半径 第 1 页（共 43 页） 选择题部分（共 40 分） 一、选择题：本大题共 10 小题，每小题 4 分，共 40 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 ð A= 1．已知全集 U={1，2，3，4，5}，A={1，3}，则 UA． B．{1，3} C．{2，4，5} D．{1，2，3，4， 5} x2 y2 =1 2．双曲线 A．(− 的焦点坐标是 322，0)，( ，0) B．(−2，0)，(2，0) D．(0，−2)，(0，2) 22)C．(0，− )，(0， 3．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是 2211侧视图 正视图 俯视图 A．2 B．4 C．6 D．8 24．复数 (i 为虚数单位)的共轭复数是 B．1−i 1 i A．1+i C．−1+i D．−1−i 2|x| 5．函数 y= sin2x 的图象可能是 第 2 页（共 43 页） A． B． C． D． 6．已知平面 α，直线 m，n 满足 m α，n α，则“m∥n”是“m∥α”的 B．必要不充分条件 A．充分不必要条件 C．充分必要条件 D．既不充分也不必要条件 7．设 0<p<1，随机变量 ξ 的分布列是 ξ0121 p 212pP2p01则当 在（， ）内增大时， A．D（ξ）减小 B．D（ξ）增大 C．D（ξ）先减小后增大 D．D（ξ）先增大后减小 8．已知四棱锥 S−ABCD 的底面是正方形，侧棱长均相等，E 是线段 AB 上的点（不含端点）， 设 SE 与 BC 所成的角为 θ1，SE 与平面 ABCD 所成的角为 θ2，二面角 S−AB−C 的平面角 为 θ3，则 A．θ1≤θ2≤θ3 B．θ3≤θ2≤θ1 C．θ1≤θ3≤θ2 D．θ2≤θ3≤θ1 第 3 页（共 43 页） π9．已知 a，b，e 是平面向量，e 是单位向量．若非零向量 a 与 e 的夹角为 ，向量b 满足 3b2−4e·b+3=0，则|a−b|的最小值是 A． −1 B． +1 C．2 D．2− a 1 333a a a a ln(a a a ) a ,a ,a ,a 4 成等比数列，且 10．已知 ．若 1，则 1234123123a a ,a a a a ,a a a a ,a a C． A． B． 132413241324a a ,a a D． 1324非选择题部分（共 110 分） 二、填空题：本大题共 7 小题，多空题每题 6 分，单空题每题 4 分，共 36 分。 11．我国古代数学著作《张邱建算经》中记载百鸡问题：“今有鸡翁一，值钱五；鸡母一， 值钱三；鸡雏三，值钱一。凡百钱，买鸡百只，问鸡翁、母、雏各几何？”设鸡翁，鸡 x y z 100, x母，鸡雏个数分别为 ， z 81 x 时， ___________， y，z，则 当15x 3y z 100, 3y ___________． x y 0, 2x y 6, x y 2, 12．若 x, y 满足约束条件 ___________． 则 z x 3y 的最小值是___________ ，最大值是 713．在△ABC 中，角 A，B，C 所对的边分别为 a，b，c．若 a= ，b=2，A=60°，则 sin B=___________，c=___________． 18 的展开式的常数项是___________． )(3 x 14．二项式 2x x 4, x x2 4x 3, x 15 ． 已 知λ ∈ R ， 函 数f(x)= ， 当λ=2 时 ， 不 等 式f(x)<0 的 解 集 是 ___________．若函数 f(x)恰有 2 个零点，则 λ 的取值范围是___________． 第 4 页（共 43 页） 16．从 1，3，5，7，9 中任取 2 个数字，从 0，2，4，6 中任取 2 个数字，一共可以组成___________ 个没有重复数字的四位数.(用数字作答) x2 4 +y2=m(m>1)上两点 A，B 满足 AP =2 PB ，则当 m=___________ 17．已知点 P(0，1)，椭圆 时，点 B 横坐标的绝对值最大． 三、解答题：本大题共 5 小题，共 74 分。解答应写出文字说明、证明过程或演算步骤。 18 14 αO分）已知角 的顶点与原点 重合，始边与轴的非负半轴重合，它的 x．（本题满分 34 ，- P终边过点 （ ）． 55sin α+π （（Ⅰ）求 ）的值； 5β（Ⅱ）若角 满足 sin α+β =cosβ ，求 的值． （）13 19 ．（本题满分 15 ABCA B CA AB BC C ABC 均垂直于平面 ，∠ 分）如图，已知多面体 ，，，111111ABC=120° A A=4 C C=1 AB=BC=B B=2 ．，，，111AB （Ⅰ）证明： 1⊥平面 A B C ；1 1 1 AC （Ⅱ）求直线 1 与平面 ABB 1 所成的角的正弦值． 20 15 {a } nq>1 a +a +a =28 a +2 a是3a， 5 的等 ．（本题满分 分）已知等比数列 的公比 ，且 ，3454差中项．数列 第 5 页（共 43 页） {b } nb =1 1{，数列 （ b−b a} n2n2+n 的前 项和为． 满足 ）n+1 nnq（Ⅰ）求 的值； {b } *（Ⅱ）求数列 的通项公式．学科网 n21．（本题满分 15 分）如图，已知点 P 是 y 轴左侧(不含 y 轴)一点，抛物线 C：y2=4x 上存在 不同的两点 A，B 满足 PA，PB 的中点均在 C 上． yAPMxOB（Ⅰ）设 AB 中点为 M，证明：PM 垂直于 y 轴； y2 （Ⅱ）若 P 是半椭圆 x2+ =1(x<0)上的动点，求△PAB 面积的取值范围． 4×22．（本题满分 15 分）已知函数 f(x)= −lnx． （Ⅰ）若 f(x)在 x=x1，x2(x1≠x2)处导数相等，证明：f(x1)+f(x2)>8−8ln2； （Ⅱ）若 a≤3−4ln2，证明：对于任意 k>0，直线 y=kx+a 与曲线 y=f(x)有唯一公共点． 2018 年普通高等学校招生全国统一考试（浙江卷） 数 学·参考答案 4一、选择题：本题考查基本知识和基本运算。每小题 分，满分 40 分。 1.C 2.B 3.C 4.B 5.D 6.A 7.D 8.D 9.A 10.B 64二、填空题：本题考查基本知识和基本运算。多空题每题 分，单空题每题 分，满分 36 分。 第 6 页（共 43 页） 21 711.8 11 ；12.−2 813. 14.7 ；;3 (1,4);(1,3] (4,) 15. 16.1260 17.5 5三、解答题：本大题共 小题，共 74 分。 18. 本题主要考查三角函数及其恒等变换等基础知识，同时考查运算求解能力。满分 14 分。 3445（Ⅰ）由角 的终边过点 P( , ) sin 得，5545sin( π) sin .所以 3435（Ⅱ）由角 的终边过点 P( , ) cos 得，55512 13 sin( ) cos( ) .由得13 ( ) cos cos( )cos sin( )sin 得 ， 由56 65 16 65 cos cos .所以 或19. 本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空 15 间想象能力和运算求解能力。满分 方法一： 分。 AB 2, AA 4, BB 2, AA AB, BB AB （Ⅰ）由 得AB A B 2 2 ，111111 1 A B2 AB2 AA2 .1所以 111AB A B .故11 1 第 7 页（共 43 页） BB 2,CC 1, BB BC,CC BC 由BC 2 ，得B C1 5 ，11111AB BC 2,ABC 120 由得，AC 2 3 CC AC ，得 AC 13 AB2 B C2 AC2 AB B C .由，所以 ，故 1111111 1 1AB A B C .1 1 1 因此 平面 1C（Ⅱ）如图，过点 1 作 C D A B A B .1 ，交直线 于点 ，连结 DAD 1111AB A B C A B C ABB ，1由由平面 1 得平面 平面 111111C D A BC D 1 得 ABB ，1平面 111C ADAC ABB 1 所成的角 学科 网 ..所以 是1 与平面 161由B C1 5, A B 2 2,AC1 21 得cosC1A B ,sin C1A B ，1111111 1 77C1D 39 sin C AD 所以 C D 3 ，故 .11AC1 13 39 AC ABB .因此，直线 方法二： 1 与平面 1 所成的角的正弦值是 13 第 8 页（共 43 页） AC O的中点 为原点，分别以射线 OB OC ，x y 为 ， 轴的正半轴，建立空 （Ⅰ）如图，以 O-xyz. 间直角坐标系 由题意知各点坐标如下： A(0, 3,0), B(1,0,0), A (0, 3,4), B (1,0,2),C1(0, 3,1), 11uuur uuuur uuuur 1因此 AB (1, 3,2),A B (1, 3,2), AC1 (0,2 3,3), 111uuur uuuur AB A B ..由得得AB A B 0 11 1 11 1 uuur uuuur AB AC 由AB AC1 0 11 1 11AB A B C .1 1 1 所以 平面 1AC ABB 1 所成的角为 .（Ⅱ）设直线 由（Ⅰ）可知 ABB 1 与平面 uuur uuur uuur AC1 (0,2 3,1),AB (1, 3,0),BB (0,0,2), 1n (x, y, z) 1 的法向量 .设平面 uuur n AB 0, x 3y 0, 2z 0, .n ( 3,1,0) 由即可取 uuur n BB 0, 1uuur uuur | AC n | 39 sin |cos AC ,n | uuur 1 .所以 113 | AC1 || n | 第 9 页（共 43 页） 39 AC ABB 1 所成的角的正弦值是 .因此，直线 1 与平面 13 20. 本题主要考查等差数列、等比数列、数列求和等基础知识，同时考查运算求解能力 15 和综合应用能力。满分 分。 a 2 a ,a a a 2a 4 （Ⅰ）由 是5 的等差中项得 ，43354a a a 3a 4 28 所以 解得 ，3454a 8 .418(q ) 20 a a 20 由得，35qq 1 q 2 .因为 （Ⅱ）设 ，所以 c (bn1 bn )a {c } Sn.n ，数列 前项和为 nnnS ,n 1, 1c c 4n 1 .由解得 nnSn Sn1,n 2. a 2n1 由（Ⅰ）可知 ，n1bn1 bn (4n 1)( )n1 所以 ，21b bn1 (4n 5)( )n2 ,n 2 故，n2bn b (bn bn1) (bn1 bn2 ) (b3 b2 ) (b2 b ) 11111 (4n 5)( )n2 (4n 9)( )n3 7 3 .222第 10 页（共 43 页） 111T 3 7 11( )2 (4n 5)( )n2 ,n 2 设，n222121111Tn 3 7( )2 (4n 9)( )n2 (4n 5)( )n1 2222121111Tn 3 4 4( )2 4( )n2 (4n 5)( )n1 所以 因此 ，22221T 14 (4n 3)( )n2 ,n 2 ，n21b 1 b 15 (4n 3)( )n2 .又，所以 1n221 ．本题主要考查椭圆、抛物线的几何性质，直线与抛物线的位置关系等基础知识，同时考 15 查运算求解能力和综合应用能力。满分 分。 11P(x , y ) A( y2 , y ) B( y2 , y ) （Ⅰ）设 ，，．00112244yy因为 ，PA PB 的中点在抛物线上，所以 ，2 为方程 11y2 x0 y2 2y y8x y2 0 y y 即的两个不同的实数根． 2(0 ) 4 400022y y 2y 所以 ．120y垂直于 轴． 因此， PM y y 2y , 120（Ⅱ）由（Ⅰ）可知 y y 8x y2 , 120013| PM | (y2 y2 ) x y02 3×0 2所以 ，．| y1 y2 | 2 2(y0 4×0 ) 12084第 11 页（共 43 页） 313 2 42因此， 的面积 ．△PAB S△PAB | PM || y1 y2 | (y0 4×0 )2 2y02 y2 4x 4×2 4x 4[4,5] 2因为 ，所以 ．x0 1(x0 0) 0000415 10 4因此， 面积的取值范围是 ．△PAB [6 2, ]22 ．本题主要考查函数的单调性，导数的运算及其应用，同时考查逻辑思维能力和综合应用 15 能力。满分 分。 11f (x) fx（Ⅰ）函数 （ ）的导函数 ，x2 x 1111f (x ) f (x ) 由得2，1×1 x2 2 x1 2 x2 1112x x 因为 2 ，所以 ．1×1 x2 1x1x2 x1 x2 24 x1x2 由基本不等式得 ．2x x x x 256 ．因为 2 ，所以 11 2 12f (x ) f (x ) x1 ln x1 x2 ln x2 x x ln(x x ) 由题意得 ．21212112g(x) g(x) x ln x 设则，1( x 4) ，4x 所以 x（0，16） 16 0（16，+∞） g(x) -+第 12 页（共 43 页） g(x) 2-4ln2 g所以 （）在 x[256 +， ∞）上单调递增， g(x x ) g(256) 8 8ln 2 故即，12f (x ) f (x ) 8 8ln 2 ．12a 1 ( a k) )2 1，则 m= n= (（Ⅱ）令 ，ekfm–km–a>|a|+k–k–a≥0 （ ）， 1an| a | 1 n( k) n( k) <0 f n （ ） –kn–a< ≤，nnxmnfx=kx +a 所以，存在 0∈（ ，）使 （） ， 00aRk0+所以，对于任意的 ∈ 及 ∈（， ∞），直线 y=kx+a y=f x （ ）有公共点． 与曲线 x ln x a fx=kx+a 由 （ ）得 k ．xx ln x a hx设 （） =，xxln x 1 a g(x) 1 a h′ = x则（ ） ，2x2 x2 xgx其中 （） = ln x ．2gx由（Ⅰ）可知 （） ≥g 16 a≤3–4ln2 （ ），又， –g x（ ） –1+a≤–g 16 –1+a=–3+4ln2+a≤0 （ ）， 故h′ –kx–a=0 x≤0 hx0+fx所以 （） ，即函数（ ）在（ ， ∞）上单调递减，因此方程 （ ）至 1多个实根． a≤3–4ln2 k>0 y=kx+a y=f x 与曲线 （）有唯一公共点． 综上，当 时，对于任意 ，直线 第 13 页（共 43 页） 第 14 页（共 43 页） 2018 年浙江省高考数学试卷 参考答案与试题解析 一、选择题：本大题共 10 小题，每小题 4 分，共 40 分。在每小题给出的四个 选项中，只有一项是符合题目要求的。 1．（4 分）已知全集 U={1，2，3，4，5}，A={1，3}，则∁UA=（ ） A．∅ B．{1，3} C．{2，4，5} D．{1，2，3，4， 5} 【考点】1F：补集及其运算．菁优网版权所有 【分析】根据补集的定义直接求解：∁UA 是由所有属于集合 U 但不属于 A 的元素 构成的集合． 【解答】解：根据补集的定义，∁UA 是由所有属于集合 U 但不属于 A 的元素构成 的集合，由已知，有且仅有 2，4，5 符合元素的条件． ∁UA={2，4，5} 故选：C． 【点评】本题考查了补集的定义以及简单求解，属于简单题． 2．（4 分）双曲线 ﹣y2=1 的焦点坐标是（ ） A．（﹣ ，0），（ ，0） B．（﹣2，0），（2，0） C．（0， ﹣），（0， ） D．（0，﹣2），（0，2） 第 15 页（共 43 页） 【考点】KC：双曲线的性质．菁优网版权所有 【专题】34：方程思想；4O：定义法；5D：圆锥曲线的定义、性质与方程． 【分析】根据双曲线方程，可得该双曲线的焦点在 x 轴上，由平方关系算出 c= =2，即可得到双曲线的焦点坐标． 【解答】解：∵双曲线方程可得双曲线的焦点在 x 轴上，且 a2=3，b2=1， 由此可得 c= =2， ∴该双曲线的焦点坐标为（±2，0） 故选：B． 【点评】本题考查双曲线焦点坐标，着重考查了双曲线的标准方程和焦点坐标求 法等知识，属于基础题． 3．（4 分）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位： cm3）是（ ） A．2 B．4 C．6 D．8 第 16 页（共 43 页） 【考点】L!：由三视图求面积、体积．菁优网版权所有 【专题】35：转化思想；5F：空间位置关系与距离． 【分析】直接利用三视图的复原图求出几何体的体积． 【解答】解：根据三视图：该几何体为底面为直角梯形的四棱柱． 如图所示： 故该几何体的体积为：V= 故选：C． ．【点评】本题考查的知识要点：三视图的应用． 4．（4 分）复数 A．1+i （i 为虚数单位）的共轭复数是（ ） B．1﹣i C．﹣1+i D．﹣1﹣i 【考点】A5：复数的运算．菁优网版权所有 【专题】5N：数系的扩充和复数． 【分析】化简已知复数 z，由共轭复数的定义可得． 【解答】解：化简可得 z= 第 17 页（共 43 页） ==1+i， ∴z 的共轭复数 =1﹣i 故选：B． 【点评】本题考查复数的代数形式的运算，涉及共轭复数，属基础题． 5．（4 分）函数 y=2|x|sin2x 的图象可能是（ ） A． B． C． D． 【考点】3A：函数的图象与图象的变换．菁优网版权所有 【专题】35：转化思想；51：函数的性质及应用． 【分析】直接利用函数的图象和性质求出结果． 【解答】解：根据函数的解析式 y=2|x|sin2x，得到：函数的图象为奇函数， 故排除 A 和 B． 第 18 页（共 43 页） 当 x= 时，函数的值也为 0， 故排除 C． 故选：D． 【点评】本题考查的知识要点：函数的性质和赋值法的应用． 6．（4 分）已知平面 α，直线 m，n 满足 m⊄α，n⊂α，则“m∥n”是“m∥α”的（ ） A．充分不必要条件 C．充分必要条件 B．必要不充分条件 D．既不充分也不必要条件 【考点】29：充分条件、必要条件、充要条件．菁优网版权所有 【专题】38：对应思想；4O：定义法；5L：简易逻辑． 【分析】根据线面平行的定义和性质以及充分条件和必要条件的定义进行判断即 可． 【解答】解：∵m⊄α，n⊂α， ∴当 m∥n 时，m∥α 成立，即充分性成立， 当 m∥α 时，m∥n 不一定成立，即必要性不成立， 则“m∥n”是“m∥α”的充分不必要条件． 故选：A． 【点评】本题主要考查充分条件和必要条件的判断，根据线面平行的定义和性质 是解决本题的关键，是基础题． 7．（4 分）设 0＜p＜1，随机变量 ξ 的分布列是 第 19 页（共 43 页） ξ012P则当 p 在（0，1）内增大时，（ ） A．D（ξ）减小 B．D（ξ）增大 C．D（ξ）先减小后增大 D．D（ξ）先增大后减小 【考点】CH：离散型随机变量的期望与方差．菁优网版权所有 【专题】33：函数思想；4O：定义法；5I：概率与统计． 【分析】求出随机变量 ξ 的分布列与方差，再讨论 D（ξ）的单调情况． 【解答】解：设 0＜p＜1，随机变量 ξ 的分布列是 E（ξ）=0× +1× +2× =p+ ； 方差是 D（ξ）= =﹣p2+p+ × + × + ×=﹣ + ， ∴p∈（0， ）时，D（ξ）单调递增； p∈（ ，1）时，D（ξ）单调递减； ∴D（ξ）先增大后减小． 故选：D． 【点评】本题考查了离散型随机变量的数学期望与方差的计算问题，也考查了运 第 20 页（共 43 页） 算求解能力，是基础题． 8．（4 分）已知四棱锥 S﹣ABCD 的底面是正方形，侧棱长均相等，E 是线段 AB 上的点（不含端点）．设 SE 与 BC 所成的角为 θ1，SE 与平面 ABCD 所成的角为 θ2，二面角 S﹣AB﹣C 的平面角为 θ3，则（ ） A．θ1≤θ2≤θ3 B．θ3≤θ2≤θ1 C．θ1≤θ3≤θ2 D．θ2≤θ3≤θ1 【考点】L3：棱锥的结构特征；LM：异面直线及其所成的角；MI：直线与平面 所成的角；MJ：二面角的平面角及求法．菁优网版权所有 【专题】31：数形结合；44：数形结合法；5G：空间角． 【分析】作出三个角，表示出三个角的正弦或正切值，根据三角函数的单调性即 可得出三个角的大小． 【解答】解：∵由题意可知 S 在底面 ABCD 的射影为正方形 ABCD 的中心． 过 E 作 EF∥BC，交 CD 于 F，过底面 ABCD 的中心 O 作 ON⊥EF 交 EF 于 N， 连接 SN， 取 AB 中点 M，连接 SM，OM，OE，则 EN=OM， 则 θ1=∠SEN，θ2=∠SEO，θ3=∠SMO． 显然，θ1，θ2，θ3 均为锐角． ∵tanθ1= =，tanθ3= ，SN≥SO， ∴θ1≥θ3， 又 sinθ3= ，sinθ2= ，SE≥SM， ∴θ3≥θ2． 第 21 页（共 43 页） 故选：D． 【点评】本题考查了空间角的计算，三角函数的应用，属于中档题． 9．（4 分）已知 ， ， 是平面向量， 是单位向量．若非零向量 与 的夹角 为，向量 满足﹣4 • +3=0，则| ﹣ |的最小值是（ ） A． ﹣1 B． +1 C．2 D．2﹣ 【考点】9O：平面向量数量积的性质及其运算．菁优网版权所有 【专题】11：计算题；31：数形结合；4R：转化法；5A：平面向量及应用． 【分析】把等式 ﹣4 • +3=0 变形，可得得 ，即（）⊥ ），设 ，则的终点在以（2，0）为圆心，以 1 为半径的圆 （周上，再由已知得到 的终点在不含端点O 的两条射线 y= （x＞0）上， 画出图形，数形结合得答案． 【解答】解：由 ﹣4 • +3=0，得 ，∴（ ）⊥（ ）， 第 22 页（共 43 页） 如图，不妨设 ，则 的终点在以（2，0）为圆心，以 1 为半径的圆周上， 又非零向量 与 的夹角为，则 的终点在不含端点O 的两条射线 y= （x＞0）上． 不妨以 y= 1． 为例，则| ﹣ |的最小值是（2，0）到直线 的距离减 即．故选：A． 【点评】本题考查平面向量的数量积运算，考查数学转化思想方法与数形结合的 解题思想方法，属难题． 10．（4 分）已知 a1，a2，a3，a4 成等比数列，且 a1+a2+a3+a4=ln（a1+a2+a3），若 a1 ＞1，则（ ） A．a1＜a3，a2＜a4 B．a1＞a3，a2＜a4 C．a1＜a3，a2＞a4 D．a1＞a3，a2＞a4 第 23 页（共 43 页） 【考点】4H：对数的运算性质；87：等比数列的性质；8I：数列与函数的综合． 菁优网版权所有 【专题】11：计算题；32：分类讨论；34：方程思想；49：综合法；51：函数的 性质及应用；54：等差数列与等比数列． 【分析】利用等比数列的性质以及对数函数的单调性，通过数列的公比的讨论分 析判断即可． 【解答】解：a1，a2，a3，a4 成等比数列，由等比数列的性质可知，奇数项符号 相同，偶数项符号相同， a1＞1，设公比为 q， 当 q＞0 时，a1+a2+a3+a4＞a1+a2+a3，a1+a2+a3+a4=ln（a1+a2+a3），不成立， 即：a1＞a3，a2＞a4，a1＜a3，a2＜a4，不成立，排除 A、D． 当 q=﹣1 时，a1+a2+a3+a4=0，ln（a1+a2+a3）＞0，等式不成立，所以 q≠﹣1； 当 q＜﹣1 时，a1+a2+a3+a4＜0，ln（a1+a2+a3）＞0，a1+a2+a3+a4=ln（a1+a2+a3）不 成立， 当 q∈（﹣1，0）时，a1＞a3＞0，a2＜a4＜0，并且 a1+a2+a3+a4=ln（a1+a2+a3），能 够成立， 故选：B． 【点评】本题考查等比数列的性质的应用，函数的值的判断，对数函数的性质， 考查发现问题解决问题的能力，难度比较大． 二、填空题：本大题共 7 小题，多空题每题 6 分，单空题每题 4 分，共 36 分。 11．（6 分）我国古代数学著作《张邱建算经》中记载百鸡问题：“今有鸡翁一， 第 24 页（共 43 页） 值钱五；鸡母一，值钱三；鸡雏三，值钱一．凡百钱，买鸡百只，问鸡翁、 母 、 雏 各 几 何 ？ ” 设 鸡 翁 ， 鸡 母 ， 鸡 雏 个 数 分 别 为x ， y ， z ， 则 ，当 z=81 时，x= 8 ，y= 11 ． 【考点】53：函数的零点与方程根的关系．菁优网版权所有 【专题】11：计算题；33：函数思想；49：综合法；51：函数的性质及应用． 【分析】直接利用方程组以及 z 的值，求解即可． 【解答】解： ，当 z=81 时，化为： ，解得 x=8，y=11． 故答案为：8；11． 【点评】本题考查方程组的解法，是基本知识的考查． 12．（6 分）若 x，y 满足约束条件 大值是 8 ． ，则 z=x+3y 的最小值是 ﹣2 ，最 【考点】7C：简单线性规划．菁优网版权所有 【专题】1：常规题型；11：计算题；35：转化思想；49：综合法；5T：不等 式． 【分析】作出题中不等式组表示的平面区域，得到如图的△ABC 及其内部，再将 目标函数 z=x+3y 对应的直线进行平移，观察直线在 y 轴上的截距变化，然后 第 25 页（共 43 页） 求解最优解得到结果． 【解答】解：作出 x，y 满足约束条件 表示的平面区域， 如图： 其中 B（4，﹣2），A（2，2）． 设 z=F（x，y）=x+3y， 将直线 l：z=x+3y 进行平移，观察直线在 y 轴上的截距变化， 可得当 l 经过点 B 时，目标函数 z 达到最小值． ∴z 最小值=F（4，﹣2）=﹣2． 可得当 l 经过点 A 时，目标函数 z 达到最最大值： z 最大值=F（2，2）=8． 故答案为：﹣2；8． 【点评】本题给出二元一次不等式组，求目标函数的最小值，着重考查了二元一 次不等式组表示的平面区域和简单的线性规划等知识，属于中档题． 第 26 页（共 43 页） 13．（6 分）在△ABC 中，角 A，B，C 所对的边分别为 a，b，c．若 a= ，b=2， A=60°，则 sinB= ，c= 3 ． 【考点】HP：正弦定理．菁优网版权所有 【专题】11：计算题；35：转化思想；49：综合法；58：解三角形． 【分析】由正弦定理得 ，由此能求出sinB，由余弦定理得 cos60°= =，由此能求出 c． 【解答】解：∵在△ABC 中，角 A，B，C 所对的边分别为 a，b，c． a= ，b=2，A=60°， ∴由正弦定理得： ，即 =，解得 sinB= =．由余弦定理得： cos60°= ，解得 c=3 或 c=﹣1（舍）， ∴sinB= ，c=3． 故答案为： ，3． 【点评】本题考查三角形中角的正弦值、边长的求法，考查正弦定理、余弦定理 等基础知识，考查运算求解能力，考查函数与方程思想，是中档题． 第 27 页（共 43 页） 14．（4 分）二项式（ + ）8 的展开式的常数项是 7 ． 【考点】DA：二项式定理．菁优网版权所有 【专题】35：转化思想；4O：定义法；5P：二项式定理． 【分析】写出二项展开式的通项并整理，由 x 的指数为 0 求得 r 值，则答案可 求． 【解答】解：由 =．令=0，得 r=2． ∴二项式（ + ）8 的展开式的常数项是 故答案为：7． ．【点评】本题考查了二项式系数的性质，关键是熟记二项展开式的通项，是基础 题． 15．（6 分）已知 λ∈R，函数 f（x）= ，当 λ=2 时，不等式 f（x）＜ 0 的解集是 {x|1＜x＜4} ．若函数 f（x）恰有 2 个零点，则 λ 的取值范围 是 （1，3]∪（4，+∞） ． 【考点】3E：函数单调性的性质与判断；57：函数与方程的综合运用；5B：分段 函数的应用．菁优网版权所有 【专题】11：计算题；31：数形结合；34：方程思想；49：综合法；51：函数的 性质及应用． 第 28 页（共 43 页） 【分析】利用分段函数转化求解不等式的解集即可；利用函数的图象，通过函数 的零点得到不等式求解即可． 【解答】解：当 λ=2 时函数 f（x）= ，显然 x≥2 时，不等式 x﹣4 ＜0 的解集：{x|2≤x＜4}；x＜2 时，不等式 f（x）＜0 化为：x2﹣4x+3＜0， 解得 1＜x＜2，综上，不等式的解集为：{x|1＜x＜4}． 函数 f（x）恰有 2 个零点， 函数 f（x）= 的草图如图： 函数 f（x）恰有 2 个零点，则 1＜λ≤3 或 λ＞4． 故答案为：{x|1＜x＜4}；（1，3]∪（4，+∞）． 【点评】本题考查函数与方程的应用，考查数形结合以及函数的零点个数的判断， 考查发现问题解决问题的能力． 16．（4 分）从 1，3，5，7，9 中任取 2 个数字，从 0，2，4，6 中任取 2 个数字， 一共可以组成 1260 个没有重复数字的四位数．（用数字作答） 第 29 页（共 43 页） 【考点】D9：排列、组合及简单计数问题．菁优网版权所有 【专题】11：计算题；35：转化思想；49：综合法；5O：排列组合． 【分析】可先从 1，3，5，7，9 中任取 2 个数字，然后通过 0 是否存在，求解即 可． 【解答】解：从 1，3，5，7，9 中任取 2 个数字有 种方法， 从 2，4，6，0 中任取 2 个数字不含 0 时，有 种方法， 可以组成 =720 个没有重复数字的四位数； 含有 0 时，0 不能在千位位置，其它任意排列，共有 =540， 故一共可以组成 1260 个没有重复数字的四位数． 故答案为：1260． 【点评】本题考查排列组合及简单的计数问题，先选后排是解决问题的关键，注 意“0“是否在 4 位数中去易错点，是中档题． 17．（4 分）已知点 P（0，1），椭圆 +y2=m（m＞1）上两点 A，B 满足 =2 ，则当 m= 5 时，点 B 横坐标的绝对值最大． 【考点】K4：椭圆的性质．菁优网版权所有 【专题】34：方程思想；48：分析法；5A：平面向量及应用；5D：圆锥曲线的 定义、性质与方程． 【分析】设 A（x1，y1），B（x2，y2），运用向量共线的坐标表示，以及点满足椭 2圆方程，求得 y1，y2，有 x2 =m﹣（ ）2，运用二次函数的最值求法，可得 第 30 页（共 43 页） 所求最大值和 m 的值． 【解答】解：设 A（x1，y1），B（x2，y2）， 由 P（0，1）， =2 ，可得﹣x1=2×2，1﹣y1=2（y2﹣1）， 即有 x1=﹣2×2，y1+2y2=3， 22又 x1 +4y1 =4m， 22即为 x2 +y1 =m，① 22×2 +4y2 =4m，② ①﹣②得（y1﹣2y2）（y1+2y2）=﹣3m， 可得 y1﹣2y2=﹣m， 解得 y1= ，y2= ，2则 m=x2 +（ ）2， 2即有 x2 =m﹣（ ）2= =，2即有 m=5 时，x2 有最大值 4， 即点 B 横坐标的绝对值最大． 故答案为：5． 【点评】本题考查椭圆的方程和应用，考查向量共线的坐标表示和方程思想、转 化思想，以及二次函数的最值的求法，属于中档题． 第 31 页（共 43 页） 三、解答题：本大题共 5 小题，共 74 分。解答应写出文字说明、证明过程或演 算步骤。 18．（14 分）已知角 α 的顶点与原点 O 重合，始边与 x 轴的非负半轴重合，它的 终边过点 P（﹣ ，﹣ ）． （Ⅰ）求 sin（α+π）的值； （Ⅱ）若角 β 满足 sin（α+β）= ，求 cosβ 的值． 【考点】G9：任意角的三角函数的定义；GP：两角和与差的三角函数．菁优网版权所有 【专题】33：函数思想；4R：转化法；56：三角函数的求值． 【分析】（Ⅰ）由已知条件即可求 r，则 sin（α+π）的值可得； （Ⅱ）由已知条件即可求 sinα，cosα，cos（α+β），再由 cosβ=cos[（α+β）﹣α]=cos （α+β）cosα+sin（α+β）sinα 代值计算得答案． 【解答】解：（Ⅰ）∵角 α 的顶点与原点 O 重合，始边与 x 轴非负半轴重合，终 边过点 P（﹣ ，﹣ ）． ∴x=﹣ ，y= ，r=|OP|= ∴sin（α+π）=﹣sinα= ，；（Ⅱ）由 x=﹣ ，y= ，r=|OP|=1， 得，，又由 sin（α+β）= ，得=，第 32 页（共 43 页） 则 cosβ=cos[ （ α+β ） ﹣α]=cos （ α+β ） cosα+sin （ α+β ） sinα= ，或 cosβ=cos[ （ α+β ） ﹣α]=cos （ α+β ） cosα+sin （ α+β ） sinα= ．∴cosβ 的值为 或．【点评】本题考查了任意角的三角函数的定义，考查了三角函数的诱导公式的应 用，是中档题． 19．（15 分）如图，已知多面体 ABCA1B1C1，A1A，B1B，C1C 均垂直于平面 ABC，∠ ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2． （Ⅰ）证明：AB1⊥平面 A1B1C1； （Ⅱ）求直线 AC1 与平面 ABB1 所成的角的正弦值． 【考点】LW：直线与平面垂直；MI：直线与平面所成的角．菁优网版权所有 【专题】31：数形结合；41：向量法；5F：空间位置关系与距离；5G：空间 角． 【分析】（I）利用勾股定理的逆定理证明 AB1⊥A1B1，AB1⊥B1C1，从而可得 AB1⊥ 第 33 页（共 43 页） 平面 A1B1C1； （II）以 AC 的中点为坐标原点建立空间坐标系，求出平面 ABB1 的法向量 ，计 算 与 的夹角即可得出线面角的大小． 【解答】（I）证明：∵A1A⊥平面 ABC，B1B⊥平面 ABC， ∴AA1∥BB1， ∵AA1=4，BB1=2，AB=2， ∴A1B1= =2 ，222又 AB1= =2 ，∴AA1 =AB1 +A1B1 ， ∴AB1⊥A1B1， 同理可得：AB1⊥B1C1， 又 A1B1∩B1C1=B1， ∴AB1⊥平面 A1B1C1． （II）解：取 AC 中点 O，过 O 作平面 ABC 的垂线 OD，交 A1C1 于 D， ∵AB=BC，∴OB⊥OC， ∵AB=BC=2，∠BAC=120°，∴OB=1，OA=OC= ，以 O 为原点，以 OB，OC，OD 所在直线为坐标轴建立空间直角坐标系如图所示： 则 A（0，﹣ ，0），B（1，0，0），B1（1，0，2），C1（0， ，1）， ∴=（1， ，0）， =（0，0，2）， =（0，2 ，1）， 设平面 ABB1 的法向量为 =（x，y，z），则 ，第 34 页（共 43 页） ∴，令 y=1 可得 =（﹣ ，1，0）， ∴cos＜ ＞= ==．设直线 AC1 与平面 ABB1 所成的角为 θ，则 sinθ=|cos＜ ＞|= ．∴直线 AC1 与平面 ABB1 所成的角的正弦值为 ．【点评】本题考查了线面垂直的判定定理，线面角的计算与空间向量的应用，属 于中档题． 20．（15 分）已知等比数列{an}的公比 q＞1，且 a3+a4+a5=28，a4+2 是 a3，a5 的 等差中项．数列{bn}满足 b1=1，数列{（bn+1﹣bn）an}的前 n 项和为 2n2+n． （Ⅰ）求 q 的值； （Ⅱ）求数列{bn}的通项公式． 【考点】8M：等差数列与等比数列的综合．菁优网版权所有 【专题】34：方程思想；48：分析法；54：等差数列与等比数列． 【分析】（Ⅰ）运用等比数列的通项公式和等差数列中项性质，解方程可得公比 第 35 页（共 43 页） q； （ Ⅱ ） 设cn= （ bn+1﹣bn ） an= （ bn+1﹣bn ） 2n﹣1 ， 运 用 数 列 的 递 推 式 可 得 cn=4n﹣1 ， 再 由 数 列 的 恒 等 式 求 得bn=b1+（ b2﹣b1 ） +（ b3﹣b2 ） +…+ （bn﹣bn﹣1），运用错位相减法，可得所求数列的通项公式． 【解答】解：（Ⅰ）等比数列{an}的公比 q＞1，且 a3+a4+a5=28，a4+2 是 a3，a5 的 等差中项， 可得 2a4+4=a3+a5=28﹣a4， 解得 a4=8， 由 +8+8q=28，可得 q=2（ 舍去）， 则 q 的值为 2； （Ⅱ）设 cn=（bn+1﹣bn）an=（bn+1﹣bn）2n﹣1 可得 n=1 时，c1=2+1=3， ，n≥2 时，可得 cn=2n2+n﹣2（n﹣1）2﹣（n﹣1）=4n﹣1， 上式对 n=1 也成立， 则（bn+1﹣bn）an=4n﹣1， 即有 bn+1﹣bn=（4n﹣1）•（ ）n﹣1 ，可得 bn=b1+（b2﹣b1）+（b3﹣b2）+…+（bn﹣bn﹣1 ），=1+3•（ ）0+7•（ ）1+…+（4n﹣5）•（ ）n﹣2 bn= +3•（ ）+7•（ ）2+…+（4n﹣5）•（ ）n﹣1 ，第 36 页（共 43 页） 相减可得 bn= +4[（ ）+（ ）2+…+（ ）n﹣2]﹣（4n﹣5）•（ ）n﹣1 = +4• ﹣（4n﹣5）•（ ）n﹣1 ，化简可得 bn=15﹣（4n+3）•（ ）n﹣2 ．【点评】本题考查等比数列的通项公式和等差数列中项的性质，考查数列的恒等 式和错位相减法的运用，考查运算能力，属于中档题． 21．（15 分）如图，已知点 P 是 y 轴左侧（不含 y 轴）一点，抛物线 C：y2=4x 上 存在不同的两点 A，B 满足 PA，PB 的中点均在 C 上． （Ⅰ）设 AB 中点为 M，证明：PM 垂直于 y 轴； （Ⅱ）若 P 是半椭圆 x2+ =1（x＜0）上的动点，求△PAB 面积的取值范围． 【考点】KL：直线与椭圆的综合；KN：直线与抛物线的综合．菁优网版权所有 【专题】34：方程思想；48：分析法；5D：圆锥曲线的定义、性质与方程． 第 37 页（共 43 页） 【分析】（Ⅰ）设 P（m，n），A（ ，y1），B（ ，y2），运用中点坐标公式 可得 M 的坐标，再由中点坐标公式和点在抛物线上，代入化简整理可得 y1， y2 为关于 y 的方程 y2﹣2ny+8m﹣n2=0 的两根，由韦达定理即可得到结论； （Ⅱ）由题意可得 m2+ =1，﹣1≤m＜0，﹣2＜n＜2，可得△PAB 面积为 S= |PM|•|y1﹣y2|，再由配方和换元法，可得面积 S 关于新元的三次函数，运用 单调性可得所求范围． 【解答】解：（Ⅰ）证明：可设 P（m，n），A（ ，y1），B（ ，y2）， AB 中点为 M 的坐标为（ ，）， 抛物线 C：y2=4x 上存在不同的两点 A，B 满足 PA，PB 的中点均在 C 上， 可得（ （）2=4• ，）2=4• ，化简可得 y1，y2 为关于 y 的方程 y2﹣2ny+8m﹣n2=0 的两根， 可得 y1+y2=2n，y1y2=8m﹣n2， 可得 n= ，则 PM 垂直于 y 轴； 第 38 页（共 43 页） （Ⅱ）若 P 是半椭圆 x2+ =1（x＜0）上的动点， 可得 m2+ =1，﹣1≤m＜0，﹣2＜n＜2， 由（Ⅰ）可得 y1+y2=2n，y1y2=8m﹣n2， 由 PM 垂直于 y 轴，可得△PAB 面积为 S= |PM|•|y1﹣y2| = （ ﹣m）• =[ •（4n2﹣16m+2n2）﹣ m]• （n2﹣4m） =，可令 t= ==，可得 m=﹣ 时，t 取得最大值 m=﹣1 时，t 取得最小值 2， ；即 2≤t≤ 则 S= ，t3 在 2≤t≤ 递增，可得S∈[6 ]． ，]， △PAB 面积的取值范围为[6 ，第 39 页（共 43 页） 【点评】本题考查抛物线的方程和运用，考查转化思想和运算能力，以及换元法 和三次函数的单调性，属于难题． 22．（15 分）已知函数 f（x）= ﹣lnx． （Ⅰ）若 f（x）在 x=x1，x2（x1≠x2）处导数相等，证明：f（x1）+f（x2）＞ 8﹣8ln2； （Ⅱ）若 a≤3﹣4ln2，证明：对于任意 k＞0，直线 y=kx+a 与曲线 y=f（x）有唯 一公共点． 【考点】6E：利用导数研究函数的最值．菁优网版权所有 【专题】14：证明题；35：转化思想；49：综合法；53：导数的综合应用． 【分析】（Ⅰ）推导出 x＞0，f′（x）= ﹣ ，由 f（x）在 x=x1，x2（x1≠x2） 处导数相等，得到 + = ，由基本不等式得： =≥，从而 x1x2＞256，由题意得 f（x1）+f（x2）= ﹣ln（x1x2），设 g（x）= ，则 =，利用导 第 40 页（共 43 页） 数性质能证明 f（x1）+f（x2）＞8﹣8ln2． （Ⅱ）令 m=e﹣（|a|+k），n=（ ）2+1，则 f（m）﹣km﹣a＞|a|+k﹣k﹣a≥0， 推导出存在 x0∈（m，n），使 f（x0）=kx0+a，对于任意的 a∈R 及 k∈（0，+∞）， 直线 y=kx+a 与曲线 y=f（x）有公共点，由 f（x）=kx+a，得 k= ，设 h（x）= ，则 h′（x）= =，利用导数性质能 证明 a≤3﹣4ln2 时，对于任意 k＞0，直线 y=kx+a 与曲线 y=f（x）有唯一公共 点． 【解答】证明：（Ⅰ）∵函数 f（x）= ﹣lnx， ∴x＞0，f′（x）= ﹣ ， ∵f（x）在 x=x1，x2（x1≠x2）处导数相等， ∴=﹣，∵x1≠x2，∴ + = ， 由基本不等式得： =≥，∵x1≠x2，∴x1x2＞256， 由题意得 f（x1）+f（x2）= =﹣ln（x1x2）， 设 g（x）= ，则 ，∴列表讨论： x16 （0，16） （16，+∞） 第 41 页（共 43 页） ﹣0g′（x） g（x） +2﹣4ln2 ↓↑∴g（x）在[256，+∞）上单调递增， ∴g（x1x2）＞g（256）=8﹣8ln2， ∴f（x1）+f（x2）＞8﹣8ln2． （Ⅱ）令 m=e﹣（|a|+k），n=（ ）2+1， 则 f（m）﹣km﹣a＞|a|+k﹣k﹣a≥0， f（n）﹣kn﹣a＜n（ ∴存在 x0∈（m，n），使 f（x0）=kx0+a， ∴对于任意的 a∈R 及 k∈（0，+∞），直线 y=kx+a 与曲线 y=f（x）有公共点， ﹣ ﹣k）≤n（ ﹣k）＜0， 由 f（x）=kx+a，得 k= 设 h（x）= ，，则 h′（x）= =，其中 g（x）= ﹣lnx， 由（1）知 g（x）≥g（16）， 又 a≤3﹣4ln2，∴﹣g（x）﹣1+a≤﹣g（16）﹣1+a=﹣3+4ln2+a≤0， ∴h′（x）≤0，即函数 h（x）在（0，+∞）上单调递减， ∴方程 f（x）﹣kx﹣a=0 至多有一个实根， 综上，a≤3﹣4ln2 时，对于任意 k＞0，直线 y=kx+a 与曲线 y=f（x）有唯一公共 第 42 页（共 43 页） 点． 【点评】本题考查函数的单调性，导数的运算及其应用，同时考查逻辑思维能力 和综合应用能力，是中档题． 第 43 页（共 43 页）
声明：如果本站提供的资源有问题或者不能下载，请点击页面底部的"联系我们"；
本站提供的资源大部分来自网络收集整理，如果侵犯了您的版权，请联系我们删除。
