
 2017 年江苏省高考数学试卷 一.填空题 1.(5 分)已知集合 A={1,2},B={a,a2+3}.若 A∩B={1},则实数 a 的值 为 . 2 .( 5 分 ) 已 知 复 数z= ( 1+i )( 1+2i ), 其 中i 是 虚 数 单 位 , 则z 的 模 是 . 3.(5 分)某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为 200, 400,300,100 件.为检验产品的质量,现用分层抽样的方法从以上所有的产品 中抽取 60 件进行检验,则应从丙种型号的产品中抽取 件. 4.(5 分)如图是一个算法流程图:若输入 x 的值为 ,则输出y 的值 是 . 5.(5 分)若 tan(α﹣ )= .则 tanα= . 6.(5 分)如图,在圆柱 O1O2 内有一个球 O,该球与圆柱的上、下底面及母线均 相切,记圆柱 O1O2 的体积为 V1,球 O 的体积为 V2,则 的值是 . 第 1 页(共 37 页) 7.(5 分)记函数 f(x)= x,则 x∈D 的概率是 定义域为 D.在区间[﹣4,5]上随机取一个数 . 8.(5 分)在平面直角坐标系 xOy 中,双曲线 ﹣y2=1 的右准线与它的两条渐 近线分别交于点 P,Q,其焦点是 F1,F2,则四边形 F1PF2Q 的面积是 . 9.(5 分)等比数列{an}的各项均为实数,其前 n 项为 Sn,已知 S3= ,S6= ,则 a8= . 10.(5 分)某公司一年购买某种货物 600 吨,每次购买 x 吨,运费为 6 万元/次, 一年的总存储费用为 4x 万元.要使一年的总运费与总存储费用之和最小,则 x 的值是 . 11.(5 分)已知函数 f(x)=x3﹣2x+ex﹣ ,其中 e 是自然对数的底数.若 f (a﹣1)+f(2a2)≤0.则实数 a 的取值范围是 12.(5 分)如图,在同一个平面内,向量 的夹角为 α,且 tanα=7, R),则 m+n= . . ,,的模分别为 1,1, ,与与的夹角为 45°.若 =m +n (m,n∈ 13.(5 分)在平面直角坐标系 xOy 中,A(﹣12,0),B(0,6),点 P 在圆 O: x2+y2=50 上.若 ≤20,则点 P 的横坐标的取值范围是 . 第 2 页(共 37 页) 14.(5 分)设 f(x)是定义在 R 上且周期为 1 的函数,在区间[0,1)上,f(x) =,其中集合 D={x|x= . ,n∈N*},则方程 f(x)﹣lgx=0 的解的个数 是 二.解答题 15.(14 分)如图,在三棱锥 A﹣BCD 中,AB⊥AD,BC⊥BD,平面 ABD⊥平面 BCD,点 E、F(E 与 A、D 不重合)分别在棱 AD,BD 上,且 EF⊥AD. 求证:(1)EF∥平面 ABC; (2)AD⊥AC. 16.(14 分)已知向量 =(cosx,sinx), =(3,﹣ ),x∈[0,π]. 第 3 页(共 37 页) (1)若 ∥ ,求x 的值; (2)记 f(x)= ,求 f(x)的最大值和最小值以及对应的 x 的值. 17.(14 分)如图,在平面直角坐标系 xOy 中,椭圆 E: =1(a>b>0) 的左、右焦点分别为 F1,F2,离心率为 ,两准线之间的距离为8.点 P 在椭圆 E 第 4 页(共 37 页) 上,且位于第一象限,过点 F1 作直线 PF1 的垂线 l1,过点 F2 作直线 PF2 的垂线 l2. (1)求椭圆 E 的标准方程; (2)若直线 l1,l2 的交点 Q 在椭圆 E 上,求点 P 的坐标. 18.(16 分)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ 的高均为 32cm,容器Ⅰ的底面对角线 AC 的长为 10 cm,容器Ⅱ的两底面对角 线 EG,E1G1 的长分别为 14cm 和 62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深 均为 12cm.现有一根玻璃棒 l,其长度为 40cm.(容器厚度、玻璃棒粗细均忽略 第 5 页(共 37 页) 不计) (1)将 l 放在容器Ⅰ中,l 的一端置于点 A 处,另一端置于侧棱 CC1 上,求 l 没 入水中部分的长度; (2)将 l 放在容器Ⅱ中,l 的一端置于点 E 处,另一端置于侧棱 GG1 上,求 l 没 入水中部分的长度. 19 .( 16 分 ) 对 于 给 定 的 正 整 数k , 若 数 列 {an} 满 足 : an﹣k+an﹣k+1+…+an﹣1+an+1+…+an+k﹣1+an+k=2kan 对任意正整数 n(n>k)总成立,则 称数列{an}是“P(k)数列”. (1)证明:等差数列{an}是“P(3)数列”; 第 6 页(共 37 页) (2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数 列. 20.(16 分)已知函数 f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数 f′ (x)的极值点是 f(x)的零点.(极值点是指函数取极值时对应的自变量的值) (1)求 b 关于 a 的函数关系式,并写出定义域; (2)证明:b2>3a; 第 7 页(共 37 页) (3)若 f(x),f′(x)这两个函数的所有极值之和不小于﹣ ,求 a 的取值范 围. 二.非选择题,附加题(21-24 选做题)【选修 4-1:几何证明选讲】(本小题满分 0 分) 21.如图,AB 为半圆 O 的直径,直线 PC 切半圆 O 于点 C,AP⊥PC,P 为垂 足. 求证:(1)∠PAC=∠CAB; 第 8 页(共 37 页) (2)AC2 =AP•AB. [选修 4-2:矩阵与变换] 22.已知矩阵 A= (1)求 AB; ,B= .(2)若曲线 C1: =1 在矩阵 AB 对应的变换作用下得到另一曲线 C2,求 C2 的方程. [选修 4-4:坐标系与参数方程] 23.在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参数), 第 9 页(共 37 页) 曲线 C 的参数方程为 (s 为参数).设 P 为曲线 C 上的动点,求点 P 到 直线 l 的距离的最小值. [选修 4-5:不等式选讲] 24.已知 a,b,c,d 为实数,且 a2+b2=4,c2+d2=16,证明 ac+bd≤8. 第 10 页(共 37 页) 【必做题】 25.如图,在平行六面体 ABCD﹣A1B1C1D1 中,AA1⊥平面 ABCD,且 AB=AD=2,AA1= ,∠BAD=120°. (1)求异面直线 A1B 与 AC1 所成角的余弦值; (2)求二面角 B﹣A1D﹣A 的正弦值. 26.已知一个口袋有 m 个白球,n 个黑球(m,n∈N*,n≥2),这些球除颜色外 全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为 1,2, 3,…,m+n 的抽屉内,其中第 k 次取出的球放入编号为 k 的抽屉(k=1,2, 3,…,m+n). 123…m+n (1)试求编号为 2 的抽屉内放的是黑球的概率 p; 第 11 页(共 37 页) (2)随机变量 x 表示最后一个取出的黑球所在抽屉编号的倒数,E(X)是 X 的 数学期望,证明 E(X)< . 第 12 页(共 37 页) 2017 年江苏省高考数学试卷 参考答案与试题解析 一.填空题 1.(5 分)(2017•江苏)已知集合 A={1,2},B={a,a2+3}.若 A∩B={1},则实 数 a 的值为 1 . 【分析】利用交集定义直接求解. 【解答】解:∵集合 A={1,2},B={a,a2+3}.A∩B={1}, ∴a=1 或 a2+3=1, 解得 a=1. 故答案为:1. 【点评】本题考查实数值的求法,是基础题,解题时要认真审题,注意交集定义 及性质的合理运用. 2.(5 分)(2017•江苏)已知复数 z=(1+i)(1+2i),其中 i 是虚数单位,则 z 的 模是 . 【分析】利用复数的运算法则、模的计算公式即可得出. 【解答】解:复数 z=(1+i)(1+2i)=1﹣2+3i=﹣1+3i, ∴|z|= =.故答案为: .【点评】本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能 力,属于基础题. 3.(5 分)(2017•江苏)某工厂生产甲、乙、丙、丁四种不同型号的产品,产量 分别为 200,400,300,100 件.为检验产品的质量,现用分层抽样的方法从以 上所有的产品中抽取 60 件进行检验,则应从丙种型号的产品中抽取 18 件. 【分析】由题意先求出抽样比例即为 ,再由此比例计算出应从丙种型号的产 第 13 页(共 37 页) 品中抽取的数目. 【解答】解:产品总数为 200+400+300+100=1000 件,而抽取 60 辆进行检验, 抽样比例为 =,则应从丙种型号的产品中抽取 300× 故答案为:18 =18 件, 【点评】本题的考点是分层抽样.分层抽样即要抽样时保证样本的结构和总体的 结构保持一致,按照一定的比例,即样本容量和总体容量的比值,在各层中进行 抽取. 4.(5 分)(2017•江苏)如图是一个算法流程图:若输入 x 的值为 ,则输出y 的值是 ﹣2 . 【分析】直接模拟程序即得结论. 【解答】解:初始值 x= ,不满足 x≥1, 所以 y=2+log2 =2﹣ 故答案为:﹣2. =﹣2, 【点评】本题考查程序框图,模拟程序是解决此类问题的常用方法,注意解题方 法的积累,属于基础题. 第 14 页(共 37 页) 5.(5 分)(2017•江苏)若 tan(α﹣ )= .则 tanα= . 【分析】直接根据两角差的正切公式计算即可 【解答】解:∵tan(α﹣ )= ==∴6tanα﹣6=tanα+1, 解得 tanα= , 故答案为: . 【点评】本题考查了两角差的正切公式,属于基础题 6.(5 分)(2017•江苏)如图,在圆柱 O1O2 内有一个球 O,该球与圆柱的上、 下底面及母线均相切,记圆柱 O1O2 的体积为 V1,球 O 的体积为 V2,则 的值 是 . 【分析】设出球的半径,求出圆柱的体积以及球的体积即可得到结果. 【解答】解:设球的半径为 R,则球的体积为: 圆柱的体积为:πR2•2R=2πR3. R3, 则== . 故答案为: . 【点评】本题考查球的体积以及圆柱的体积的求法,考查空间想象能力以及计算 第 15 页(共 37 页) 能力. 7.(5 分)(2017•江苏)记函数 f(x)= 定义域为 D.在区间[﹣4,5]上 随机取一个数 x,则 x∈D 的概率是 . 【分析】求出函数的定义域,结合几何概型的概率公式进行计算即可. 【解答】解:由 6+x﹣x2≥0 得 x2﹣x﹣6≤0,得﹣2≤x≤3, 则 D=[﹣2,3], 则在区间[﹣4,5]上随机取一个数 x,则 x∈D 的概率 P= = , 故答案为: 【点评】本题主要考查几何概型的概率公式的计算,结合函数的定义域求出 D, 以及利用几何概型的概率公式是解决本题的关键. 8.(5 分)(2017•江苏)在平面直角坐标系 xOy 中,双曲线 ﹣y2=1 的右准线 与它的两条渐近线分别交于点 P,Q,其焦点是 F1,F2,则四边形 F1PF2Q 的面积 是 . 【分析】求出双曲线的准线方程和渐近线方程,得到 P,Q 坐标,求出焦点坐标, 然后求解四边形的面积. 【解答】解:双曲线 ﹣y2=1 的右准线:x= ,双曲线渐近线方程为:y= x, 所以 P( ,),Q( ,﹣ ),F1(﹣2,0).F2(2,0). 则四边形 F1PF2Q 的面积是: 故答案为:2 =2 ..【点评】本题考查双曲线的简单性质的应用,考查计算能力. 9.(5 分)(2017•江苏)等比数列{an}的各项均为实数,其前 n 项为 Sn,已知 S3= ,S6= ,则 a8= 32 . 第 16 页(共 37 页) 【分析】设等比数列{an}的公比为 q≠1,S3= ,S6= ,可得 = , =,联立解出即可得出. 【解答】解:设等比数列{an}的公比为 q≠1, ∵S3= ,S6= ,∴ 解得 a1= ,q=2. = , =,则 a8= =32. 故答案为:32. 【点评】本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能 力,属于中档题. 10.(5 分)(2017•江苏)某公司一年购买某种货物 600 吨,每次购买 x 吨,运 费为 6 万元/次,一年的总存储费用为 4x 万元.要使一年的总运费与总存储费用 之和最小,则 x 的值是 30 . 【分析】由题意可得:一年的总运费与总存储费用之和= +4x,利用基本 不等式的性质即可得出. 【解答】解:由题意可得:一年的总运费与总存储费用之和= +4x≥4×2× =240(万元). 当且仅当 x=30 时取等号. 故答案为:30. 【点评】本题考查了基本不等式的性质及其应用,考查了推理能力与计算能力, 属于基础题. 11.(5 分)(2017•江苏)已知函数 f(x)=x3﹣2x+ex﹣ ,其中 e 是自然对数 的底数.若 f(a﹣1)+f(2a2)≤0.则实数 a 的取值范围是 [﹣1, ] . 第 17 页(共 37 页) 【分析】求出 f(x)的导数,由基本不等式和二次函数的性质,可得 f(x)在 R 上递增;再由奇偶性的定义,可得 f(x)为奇函数,原不等式即为 2a2≤1﹣a, 运用二次不等式的解法即可得到所求范围. 【解答】解:函数 f(x)=x3﹣2x+ex﹣ 的导数为: f′(x)=3×2﹣2+ex+ ≥﹣2+2 =0, 可得 f(x)在 R 上递增; 又 f(﹣x)+f(x)=(﹣x)3+2x+e﹣x﹣ex+x3﹣2x+ex﹣ =0, 可得 f(x)为奇函数, 则 f(a﹣1)+f(2a2)≤0, 即有 f(2a2)≤﹣f(a﹣1)=f(1﹣a), 即有 2a2≤1﹣a, 解得﹣1≤a≤ , 故答案为:[﹣1, ]. 【点评】本题考查函数的单调性和奇偶性的判断和应用,注意运用导数和定义法, 考查转化思想的运用和二次不等式的解法,考查运算能力,属于中档题. 12.(5 分)(2017•江苏)如图,在同一个平面内,向量 1,1, 的夹角为α,且 tanα=7, 的夹角为45°.若 =m +n (m,n∈R),则 m+n= 3 . ,,的模分别为 ,与与【分析】如图所示,建立直角坐标系.A(1,0).由 与的夹角为 α,且 第 18 页(共 37 页) tanα=7.可得 cosα= (α+45°)= .B ,sinα= .C .可得 cos(α+45°)= .sin .利用 =m +n (m,n∈R),即可得出. 【解答】解:如图所示,建立直角坐标系.A(1,0). 的夹角为 α,且 tanα=7. 由与∴cosα= ∴C ,sinα= ..cos(α+45°)= (cosα﹣sinα)= sin(α+45°)= (sinα+cosα)= . .∴B .∵=m +n (m,n∈R), ∴ =m﹣ n, =0+ n, 解得 n= ,m= . 则 m+n=3. 故答案为:3. 【点评】本题考查了向量坐标运算性质、和差公式,考查了推理能力与计算能力, 属于中档题. 13.(5 分)(2017•江苏)在平面直角坐标系 xOy 中,A(﹣12,0),B(0,6), 点 P 在圆 O:x2+y2=50 上.若 ,1] . ≤20,则点 P 的横坐标的取值范围是 [﹣5 第 19 页(共 37 页) 【分析】根据题意,设 P(x0,y0),由数量积的坐标计算公式化简变形可得 2×0+y0+5≤0,分析可得其表示表示直线 2x+y+5≤0 以及直线下方的区域,联立直 线与圆的方程可得交点的横坐标,结合图形分析可得答案. 22【解答】解:根据题意,设 P(x0,y0),则有 x0 +y0 =50, = ( ﹣12﹣x0 , ﹣y0 ) • ( ﹣x0 , 6﹣y0 ) = ( 12+x0 ) x0﹣y0 ( 6﹣y0 ) 22=12×0+6y+x0 +y0 ≤20, 化为:12×0﹣6y0+30≤0, 即 2×0﹣y0+5≤0,表示直线 2x+y+5≤0 以及直线下方的区域, 联立 ,解可得 x0=﹣5 或 x0=1, 结合图形分析可得:点 P 的横坐标 x0 的取值范围是[﹣5 ,1], 故答案为:[﹣5 ,1]. 【点评】本题考查数量积的运算以及直线与圆的位置关系,关键是利用数量积化 简变形得到关于 x0、y0 的关系式. 14.(5 分)(2017•江苏)设 f(x)是定义在 R 上且周期为 1 的函数,在区间[0, 1)上,f(x)= ,其中集合 D={x|x= ,n∈N*},则方程 f(x)﹣lgx=0 的解的个数是 8 . 【分析】由已知中 f(x)是定义在 R 上且周期为 1 的函数,在区间[0,1)上,f 第 20 页(共 37 页) (x)= ,其中集合 D={x|x= ,n∈N*},分析 f(x)的图象与 y=lgx 图象交点的个数,进而可得答案. 【解答】解:∵在区间[0,1)上,f(x)= ,第一段函数上的点的横纵坐标均为有理数, 又 f(x)是定义在 R 上且周期为 1 的函数, ∴在区间[1,2)上,f(x)= ,此时 f(x)的图象与 y=lgx 有且 只有一个交点; 同理: 区间[2,3)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[3,4)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[4,5)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[5,6)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[6,7)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[7,8)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[8,9)上,f(x)的图象与 y=lgx 有且只有一个交点; 在区间[9,+∞)上,f(x)的图象与 y=lgx 无交点; 故 f(x)的图象与 y=lgx 有 8 个交点; 即方程 f(x)﹣lgx=0 的解的个数是 8, 故答案为:8 【点评】本题考查的知识点是根的存在性及根的个数判断,函数的图象和性质, 转化思想,难度中档. 二.解答题 15.(14 分)(2017•江苏)如图,在三棱锥 A﹣BCD 中,AB⊥AD,BC⊥BD,平 面 ABD⊥平面 BCD,点 E、F(E 与 A、D 不重合)分别在棱 AD,BD 上,且 EF⊥ AD. 第 21 页(共 37 页) 求证:(1)EF∥平面 ABC; (2)AD⊥AC. 【分析】(1)利用 AB∥EF 及线面平行判定定理可得结论; (2)通过取线段 CD 上点 G,连结 FG、EG 使得 FG∥BC,则 EG∥AC,利用线面 垂直的性质定理可知 FG⊥AD,结合线面垂直的判定定理可知 AD⊥平面 EFG,从 而可得结论. 【解答】证明:(1)因为 AB⊥AD,EF⊥AD,且 A、B、E、F 四点共面, 所以 AB∥EF, 又因为 EF⊊平面 ABC,AB⊆平面 ABC, 所以由线面平行判定定理可知:EF∥平面 ABC; (2)在线段 CD 上取点 G,连结 FG、EG 使得 FG∥BC,则 EG∥AC, 因为 BC⊥BD,所以 FG∥BC, 又因为平面 ABD⊥平面 BCD, 所以 FG⊥平面 ABD,所以 FG⊥AD, 又因为 AD⊥EF,且 EF∩FG=F, 所以 AD⊥平面 EFG,所以 AD⊥EG, 故 AD⊥AC. 【点评】本题考查线面平行及线线垂直的判定,考查空间想象能力,考查转化思 想,涉及线面平行判定定理,线面垂直的性质及判定定理,注意解题方法的积累, 属于中档题. 第 22 页(共 37 页) 16.(14 分)(2017•江苏)已知向量 =(cosx,sinx), =(3,﹣ ),x∈[0, π]. (1)若 ∥ ,求x 的值; (2)记 f(x)= ,求 f(x)的最大值和最小值以及对应的 x 的值. 【分析】(1)根据向量的平行即可得到 tanx=﹣ ,问题得以解决, (2)根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出 【解答】解:(1)∵ =(cosx,sinx), =(3,﹣ ), ∥ , ∴﹣ cosx=3sinx, ∴tanx=﹣ ,∵x∈[0,π], ∴x= ,(2)f(x)= =3cosx﹣ sinx=2 (cosx﹣ sinx)=2 cos(x+ ), ∵x∈[0,π], ∴x+ ∈[ , ], ∴﹣1≤cos(x+ )≤ ,当 x=0 时,f(x)有最大值,最大值 3, 当 x= 时,f(x)有最小值,最大值﹣2 .【点评】本题考查了向量的平行和向量的数量积以及三角函数的化简和三角函 数的性质,属于基础题 17.(14 分)(2017•江苏)如图,在平面直角坐标系 xOy 中,椭圆 E: =1 (a>b>0)的左、右焦点分别为 F1,F2,离心率为 ,两准线之间的距离为 8.点 P 在椭圆 E 上,且位于第一象限,过点 F1 作直线 PF1 的垂线 l1,过点 F2 作 第 23 页(共 37 页) 直线 PF2 的垂线 l2. (1)求椭圆 E 的标准方程; (2)若直线 l1,l2 的交点 Q 在椭圆 E 上,求点 P 的坐标. 【分析】(1)由椭圆的离心率公式求得 a=2c,由椭圆的准线方程 x=± ,则 2 ×=8,即可求得 a 和 c 的值,则 b2=a2﹣c2=3,即可求得椭圆方程; (2)设 P 点坐标,分别求得直线 PF2 的斜率及直线 PF1 的斜率,则即可求得 l2 22及 l1 的斜率及方程,联立求得 Q 点坐标,由 Q 在椭圆方程,求得 y0 =x0 ﹣1,联 立即可求得 P 点坐标; 方法二:设 P(m,n),当 m≠1 时, =,=,求得直线 l1 及 l1 的方程,联立求得 Q 点坐标,根据对称性可得 求得 P 点坐标. =±n2,联立椭圆方程,即可 【解答】解:(1)由题意可知:椭圆的离心率 e= = ,则 a=2c,① 椭圆的准线方程 x=± ,由 2× =8,② 由①②解得:a=2,c=1, 则 b2=a2﹣c2=3, ∴椭圆的标准方程: ;(2)方法一:设 P(x0,y0),则直线 PF2 的斜率 =,则直线 l2 的斜率 k2=﹣ ,直线 l2 的方程 y=﹣ (x﹣1), 第 24 页(共 37 页) 直线 PF1 的斜率 =,则直线 l2 的斜率 k2=﹣ ,直线 l2 的方程 y=﹣ (x+1), 联立 ,解得: ,则 Q(﹣x0, ), 由 P,Q 在椭圆上,P,Q 的横坐标互为相反数,纵坐标应相等,则 y0= ,22∴y0 =x0 ﹣1, 则,解得: ,则 ,又 P 在第一象限,所以 P 的坐标为: P( ). ,方法二:设 P(m,n),由 P 在第一象限,则 m>0,n>0, 当 m=1 时, 当 m≠1 时, 不存在,解得:Q 与 F1 重合,不满足题意, =,=,第 25 页(共 37 页) 由 l1⊥PF1,l2⊥PF2,则 =﹣ ,=﹣ ,直线 l1 的方程 y=﹣ (x+1),①直线 l2 的方程 y=﹣ (x﹣1),② 联立解得:x=﹣m,则 Q(﹣m, 由 Q 在椭圆方程,由对称性可得: 即 m2﹣n2=1,或 m2+n2=1, ), =±n2, 由 P(m,n),在椭圆方程, ,解得: ,或 ,无 解, 又 P 在第一象限,所以 P 的坐标为: P( ,). 【点评】本题考查椭圆的标准方程,直线与椭圆的位置关系,考查直线的斜率公 式,考查数形结合思想,考查计算能力,属于中档题. 18.(16 分)(2017•江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台 形玻璃容器Ⅱ的高均为 32cm,容器Ⅰ的底面对角线 AC 的长为 10 cm,容器Ⅱ 的两底面对角线 EG,E1G1 的长分别为 14cm 和 62cm.分别在容器Ⅰ和容器Ⅱ中 注入水,水深均为 12cm.现有一根玻璃棒 l,其长度为 40cm.(容器厚度、玻璃 棒粗细均忽略不计) (1)将 l 放在容器Ⅰ中,l 的一端置于点 A 处,另一端置于侧棱 CC1 上,求 l 没 入水中部分的长度; (2)将 l 放在容器Ⅱ中,l 的一端置于点 E 处,另一端置于侧棱 GG1 上,求 l 没 入水中部分的长度. 第 26 页(共 37 页) 【分析】(1)设玻璃棒在 CC1 上的点为 M,玻璃棒与水面的交点为 N,过 N 作 NP ∥MC,交 AC 于点 P,推导出 CC1 ⊥平面 ABCD,CC1 ⊥AC,NP⊥AC,求出 MC=30cm,推导出△ANP∽△AMC,由此能出玻璃棒 l 没入水中部分的长度. (2)设玻璃棒在 GG1 上的点为 M,玻璃棒与水面的交点为 N,过点 N 作 NP⊥ EG,交 EG 于点 P,过点 E 作 EQ⊥E1G1,交 E1G1 于点 Q,推导出 EE1G1G 为等腰 梯形,求出 E1Q=24cm,E1E=40cm,由正弦定理求出 sin∠GEM= ,由此能求出 玻璃棒 l 没入水中部分的长度. 【解答】解:(1)设玻璃棒在 CC1 上的点为 M,玻璃棒与水面的交点为 N, 在平面 ACM 中,过 N 作 NP∥MC,交 AC 于点 P, ∵ABCD﹣A1B1C1D1 为正四棱柱,∴CC1⊥平面 ABCD, 又∵AC⊂平面 ABCD,∴CC1⊥AC,∴NP⊥AC, ∴NP=12cm,且 AM2=AC2+MC2,解得 MC=30cm, ∵NP∥MC,∴△ANP∽△AMC, ∴=,,得 AN=16cm. ∴玻璃棒 l 没入水中部分的长度为 16cm. (2)设玻璃棒在 GG1 上的点为 M,玻璃棒与水面的交点为 N, 在平面 E1EGG1 中,过点 N 作 NP⊥EG,交 EG 于点 P, 过点 E 作 EQ⊥E1G1,交 E1G1 于点 Q, ∵EFGH﹣E1F1G1H1 为正四棱台,∴EE1=GG1,EG∥E1G1, EG≠E1G1, ∴EE1G1G 为等腰梯形,画出平面 E1EGG1 的平面图, ∵E1G1=62cm,EG=14cm,EQ=32cm,NP=12cm, 第 27 页(共 37 页) ∴E1Q=24cm, 由勾股定理得:E1E=40cm, ∴sin∠EE1G1= ,sin∠EGM=sin∠EE1G1= ,cos ,根据正弦定理得: =,∴sin ,cos ,∴sin∠GEM=sin(∠EGM+∠EMG)=sin∠EGMcos∠EMG+cos∠EGMsin∠EMG= , ∴EN= =20cm. =∴玻璃棒 l 没入水中部分的长度为 20cm. 【点评】本题考查玻璃棒 l 没入水中部分的长度的求法,考查空间中线线、线面、 面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能 力,考查数形结合思想、化归与转化思想,是中档题. 19 .( 16 分 )( 2017• 江 苏 ) 对 于 给 定 的 正 整 数k , 若 数 列 {an} 满 足 : an﹣k+an﹣k+1+…+an﹣1+an+1+…+an+k﹣1+an+k=2kan 对任意正整数 n(n>k)总成立,则 称数列{an}是“P(k)数列”. (1)证明:等差数列{an}是“P(3)数列”; (2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数 第 28 页(共 37 页) 列. 【分析】(1)由题意可知根据等差数列的性质,an﹣3+an﹣2+an﹣1+an+1+an+2+an+3 =(an﹣3+an+3)+(an﹣2+an+2)+(an﹣1+an+1)═2×3an,根据“P(k)数列”的定义, 可得数列{an}是“P(3)数列”; ( 2 ) 由 “P ( k ) 数 列 ” 的 定 义 , 则an﹣2+an﹣1+an+1+an+2=4an , an﹣3+an﹣2+an﹣1+an+1+an+2+an+3=6an,变形整理即可求得 2an=an﹣1+an+1,即可证明 数列{an}是等差数列. 【解答】解:(1)证明:设等差数列{an}首项为 a1,公差为 d,则 an=a1+(n﹣1) d, 则 an﹣3+an﹣2+an﹣1+an+1+an+2+an+3, =(an﹣3+an+3)+(an﹣2+an+2)+(an﹣1+an+1), =2an+2an+2an, =2×3an, ∴等差数列{an}是“P(3)数列”; (2)证明:由数列{an}是“P(2)数列”则 an﹣2+an﹣1+an+1+an+2=4an,① 数列{an}是“P(3)数列”an﹣3+an﹣2+an﹣1+an+1+an+2+an+3=6an,② 由①可知:an﹣3+an﹣2+an+an+1=4an﹣1,③ an﹣1+an+an+2+an+3=4an+1,④ 由②﹣(③+④):﹣2an=6an﹣4an﹣1﹣4an+1, 整理得:2an=an﹣1+an+1, ∴数列{an}是等差数列. 【点评】本题考查等差数列的性质,考查数列的新定义的性质,考查数列的运算, 考查转化思想,属于中档题. 20.(16 分)(2017•江苏)已知函数 f(x)=x3+ax2+bx+1(a>0,b∈R)有极值, 第 29 页(共 37 页) 且导函数 f′(x)的极值点是 f(x)的零点.(极值点是指函数取极值时对应的自 变量的值) (1)求 b 关于 a 的函数关系式,并写出定义域; (2)证明:b2>3a; (3)若 f(x),f′(x)这两个函数的所有极值之和不小于﹣ ,求 a 的取值范 围. 【分析】(1)通过对 f(x)=x3+ax2+bx+1 求导可知 g(x)=f′(x)=3×2+2ax+b,进 而再求导可知 g′(x)=6x+2a,通过令 g′(x)=0 进而可知 f′(x)的极小值点为 x=﹣ ,从而 f(﹣ )=0,整理可知 b= (a>0,b∈R)有极值可知 f′(x)=0 有两个不等的实根,进而可知 a>3. (2 )通过(1 )构造函数 h (a )=b2﹣3a= (4a3﹣27 ) + (a>0),结合 f(x)=x3+ax2+bx+1 ﹣+=(a3﹣27),结合 a>3 可知 h(a)>0,从而可得结论; (3)通过(1)可知 f′(x)的极小值为 f′(﹣ )=b﹣ ,利用韦达定理及完 全平方关系可知 y=f(x)的两个极值之和为 +2,进而问题转化为解不 等式 b﹣ +2= ﹣ ≥﹣ ,因式分解即得结论. ﹣+﹣【解答】(1)解:因为 f(x)=x3+ax2+bx+1, 所以 g(x)=f′(x)=3×2+2ax+b,g′(x)=6x+2a, 令 g′(x)=0,解得 x=﹣ . 由于当 x>﹣ 时 g′(x)>0,g(x)=f′(x)单调递增;当 x<﹣ 时 g′(x)< 0,g(x)=f′(x)单调递减; 所以 f′(x)的极小值点为 x=﹣ , 由于导函数 f′(x)的极值点是原函数 f(x)的零点, 所以 f(﹣ )=0,即﹣ 所以 b= + (a>0). +﹣+1=0, 因为 f(x)=x3+ax2+bx+1(a>0,b∈R)有极值, 第 30 页(共 37 页) 所以 f′(x)=3×2+2ax+b=0 有两个不等的实根, 所以 4a2﹣12b>0,即 a2﹣ + >0,解得 a>3, 所以 b= + (a>3). (2 )证明:由(1 )可知 h (a )=b2﹣3a= ﹣+=(4a3﹣27 ) (a3﹣27), 由于 a>3,所以 h(a)>0,即 b2>3a; (3)解:由(1)可知 f′(x)的极小值为 f′(﹣ )=b﹣ 设 x1,x2 是 y=f(x)的两个极值点,则 x1+x2= 所以 f(x1)+f(x2)= +a( )+b(x1+x2)+2 =(x1+x2)[(x1+x2)2﹣3x1x2]+a[(x1+x2)2﹣2x1x2]+b(x1+x2)+2 +2, 又因为 f(x),f′(x)这两个函数的所有极值之和不小于﹣ , 所以 b﹣ +2= ﹣ ≥﹣ , ,,x1x2= , ++=﹣+﹣因为 a>3,所以 2a3﹣63a﹣54≤0, 所以 2a(a2﹣36)+9(a﹣6)≤0, 所以(a﹣6)(2a2+12a+9)≤0, 由于 a>3 时 2a2+12a+9>0, 所以 a﹣6≤0,解得 a≤6, 所以 a 的取值范围是(3,6]. 【点评】本题考查利用导数研究函数的单调性、极值,考查运算求解能力,考查 转化思想,注意解题方法的积累,属于难题. 二.非选择题,附加题(21-24 选做题)【选修 4-1:几何证明选讲】(本小题满分 0 分) 第 31 页(共 37 页) 21.(2017•江苏)如图,AB 为半圆 O 的直径,直线 PC 切半圆 O 于点 C,AP⊥ PC,P 为垂足. 求证:(1)∠PAC=∠CAB; (2)AC2 =AP•AB. 【分析】(1)利用弦切角定理可得:∠ACP=∠ABC.利用圆的性质可得∠ ACB=90°.再利用三角形内角和定理即可证明. (2)由(1)可得:△APC∽△ACB,即可证明. 【解答】证明:(1)∵直线 PC 切半圆 O 于点 C,∴∠ACP=∠ABC. ∵AB 为半圆 O 的直径,∴∠ACB=90°. ∵AP⊥PC,∴∠APC=90°. ∴∠PAC=90°﹣∠ACP,∠CAB=90°﹣∠ABC, ∴∠PAC=∠CAB. (2)由(1)可得:△APC∽△ACB, ∴=.∴AC2 =AP•AB. 【点评】本题考查了弦切角定理、圆的性质、三角形内角和定理、三角形相似的 判定与性质定理,考查了推理能力与计算能力,属于中档题. [选修 4-2:矩阵与变换] 22.(2017•江苏)已知矩阵 A= (1)求 AB; ,B= .第 32 页(共 37 页) (2)若曲线 C1: =1 在矩阵 AB 对应的变换作用下得到另一曲线 C2,求 C2 的方程. 【分析】(1)按矩阵乘法规律计算; (2)求出变换前后的坐标变换规律,代入曲线 C1 的方程化简即可. 【解答】解:(1)AB= =,(2)设点 P(x,y)为曲线 C1 的任意一点, 点 P 在矩阵 AB 的变换下得到点 P′(x0,y0), 则=,即 x0=2y,y0=x, ∴x=y0,y= ,22∴,即 x0 +y0 =8, ∴曲线 C2 的方程为 x2+y2=8. 【点评】本题考查了矩阵乘法与矩阵变换,属于中档题. [选修 4-4:坐标系与参数方程] 23.(2017•江苏)在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参数),曲线 C 的参数方程为 (s 为参数).设 P 为曲线 C 上的动 点,求点 P 到直线 l 的距离的最小值. 【分析】求出直线 l 的直角坐标方程,代入距离公式化简得出距离 d 关于参数 s 的函数,从而得出最短距离. 【解答】解:直线 l 的直角坐标方程为 x﹣2y+8=0, ∴P 到直线 l 的距离 d= =,∴当 s= 时,d 取得最小值 =.【点评】本题考查了参数方程的应用,属于基础题. 第 33 页(共 37 页) [选修 4-5:不等式选讲] 24.(2017•江苏)已知 a,b,c,d 为实数,且 a2+b2=4,c2+d2=16,证明 ac+bd≤ 8. 【分析】a2+b2=4,c2+d2=16,令 a=2cosα,b=2sinα,c=4cosβ,d=4sinβ.代入 ac+bd 2化简,利用三角函数的单调性即可证明.另解:由柯西不等式可得:(ac+bd)≤ (a2+b2)(c2+d2),即可得出. 【解答】证明:∵a2+b2=4,c2+d2=16, 令 a=2cosα,b=2sinα,c=4cosβ,d=4sinβ. ∴ac+bd=8(cosαcosβ+sinαsinβ)=8cos(α﹣β)≤8.当且仅当 cos(α﹣β)=1 时 取等号. 因此 ac+bd≤8. 另解:由柯西不等式可得:(ac+bd)2≤(a2+b2)(c2+d2)=4×16=64,当且仅当 时取等号. ∴﹣8≤ac+bd≤8. 【点评】本题考查了对和差公式、三角函数的单调性、不等式的性质,考查了推 理能力与计算能力,属于中档题. 【必做题】 25.(2017•江苏)如图,在平行六面体 ABCD﹣A1B1C1D1 中,AA1⊥平面 ABCD, 且 AB=AD=2,AA1= ,∠BAD=120°. (1)求异面直线 A1B 与 AC1 所成角的余弦值; (2)求二面角 B﹣A1D﹣A 的正弦值. 【分析】在平面 ABCD 内,过 A 作 Ax⊥AD,由 AA1⊥平面 ABCD,可得 AA1⊥Ax, 第 34 页(共 37 页) AA1⊥AD,以 A 为坐标原点,分别以 Ax、AD、AA1 所在直线为 x、y、z 轴建立空 间直角坐标系.结合已知求出 A,B,C,D,A1,C1 的坐标,进一步求出 ,,,的坐标. (1)直接利用两法向量所成角的余弦值可得异面直线 A1B 与 AC1 所成角的余弦 值; (2)求出平面 BA1D 与平面 A1AD 的一个法向量,再由两法向量所成角的余弦值 求得二面角 B﹣A1D﹣A 的余弦值,进一步得到正弦值. 【解答】解:在平面 ABCD 内,过 A 作 Ax⊥AD, ∵AA1⊥平面 ABCD,AD、Ax⊂平面 ABCD, ∴AA1⊥Ax,AA1⊥AD, 以 A 为坐标原点,分别以 Ax、AD、AA1 所在直线为 x、y、z 轴建立空间直角坐标 系. ∵AB=AD=2,AA1= ,∠BAD=120°, ∴A(0,0,0),B( D(0,2,0), A1(0,0, ),C1( = ( ),C( ,1,0), ). ), = ( ), ,.(1)∵cos< >= =.∴异面直线 A1B 与 AC1 所成角的余弦值为 ; (2)设平面 BA1D 的一个法向量为 ,由,得 ,取 x= ,得 ;取平面 A1AD 的一个法向量为 .第 35 页(共 37 页) ∴cos< >= =.∴ 二 面 角B﹣A1D﹣A 的 正 弦 值 为, 则 二 面 角B﹣A1D﹣A 的 正 弦 值 为 .【点评】本题考查异面直线所成的角与二面角,训练了利用空间向量求空间角, 是中档题. 26.(2017•江苏)已知一个口袋有 m 个白球,n 个黑球(m,n∈N*,n≥2),这 些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编 号为 1,2,3,…,m+n 的抽屉内,其中第 k 次取出的球放入编号为 k 的抽屉 (k=1,2,3,…,m+n). 123…m+n (1)试求编号为 2 的抽屉内放的是黑球的概率 p; (2)随机变量 x 表示最后一个取出的黑球所在抽屉编号的倒数,E(X)是 X 的 数学期望,证明 E(X)< .【分析】(1)设事件 Ai 表示编号为 i 的抽屉里放的是黑球,则 p=p(A2)=P (A2|A1)P(A1)+P(A2| )P( ),由此能求出编号为2 的抽屉内放的是黑 球的概率. (2)X 的所有可能取值为 ,…, ,P(x= )= ,k=n,n+1, n+2,…,n+m,从而 E(X)= ()= ,由此能证明 E 第 36 页(共 37 页) (X)< .【解答】解:(1)设事件 Ai 表示编号为 i 的抽屉里放的是黑球, 则 p=p(A2)=P(A2|A1)P(A1)+P(A2| )P( )===.证明:(2)∵X 的所有可能取值为 ,…, ,P(x= )= ∴E(X)= ,k=n,n+1,n+2,…,n+m, ()= ==<=•( )==,∴E(X)< .【点评】本题考查概率的求法,考查离散型随机变量的分布列、数学期望等基础 知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、 化归与转化思想,是中档题. 第 37 页(共 37 页)
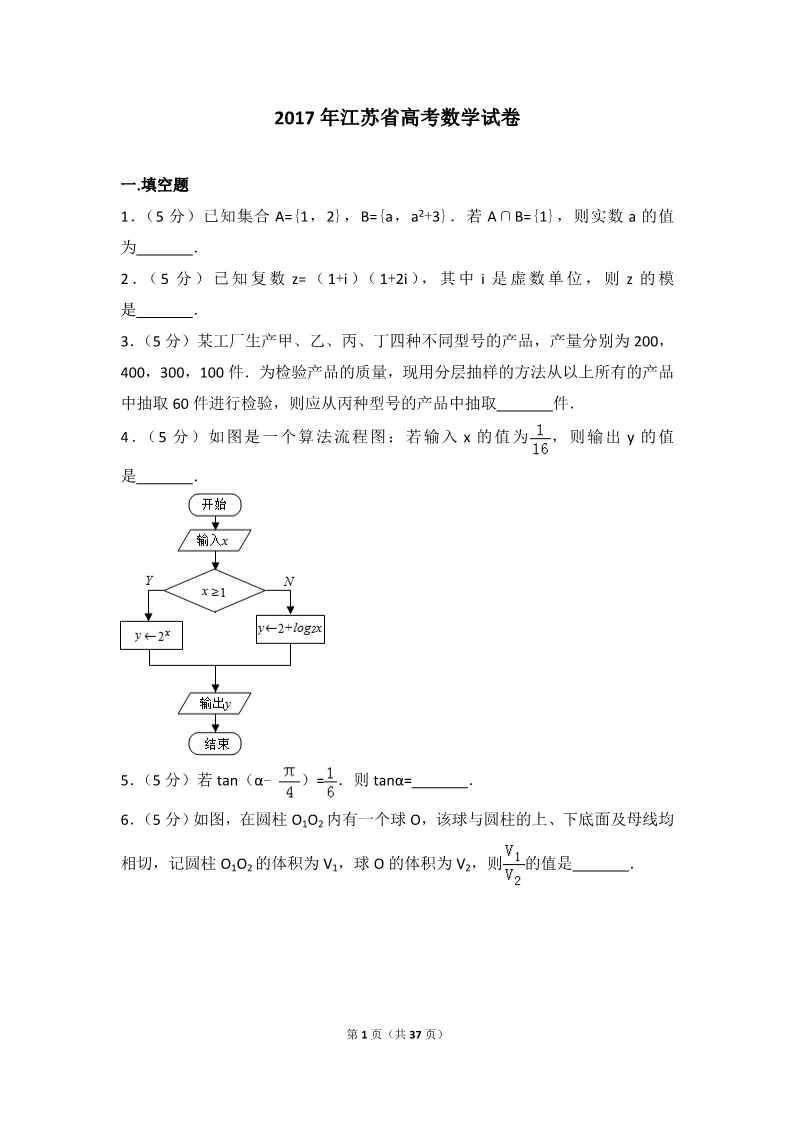
2017 年江苏省高考数学试卷 一.填空题 1.(5 分)已知集合 A={1,2},B={a,a2+3}.若 A∩B={1},则实数 a 的值 为 . 2 .( 5 分 ) 已 知 复 数z= ( 1+i )( 1+2i ), 其 中i 是 虚 数 单 位 , 则z 的 模 是 . 3.(5 分)某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为 200, 400,300,100 件.为检验产品的质量,现用分层抽样的方法从以上所有的产品 中抽取 60 件进行检验,则应从丙种型号的产品中抽取 件. 4.(5 分)如图是一个算法流程图:若输入 x 的值为 ,则输出y 的值 是 . 5.(5 分)若 tan(α﹣ )= .则 tanα= . 6.(5 分)如图,在圆柱 O1O2 内有一个球 O,该球与圆柱的上、下底面及母线均 相切,记圆柱 O1O2 的体积为 V1,球 O 的体积为 V2,则 的值是 . 第 1 页(共 37 页) 7.(5 分)记函数 f(x)= x,则 x∈D 的概率是 定义域为 D.在区间[﹣4,5]上随机取一个数 . 8.(5 分)在平面直角坐标系 xOy 中,双曲线 ﹣y2=1 的右准线与它的两条渐 近线分别交于点 P,Q,其焦点是 F1,F2,则四边形 F1PF2Q 的面积是 . 9.(5 分)等比数列{an}的各项均为实数,其前 n 项为 Sn,已知 S3= ,S6= ,则 a8= . 10.(5 分)某公司一年购买某种货物 600 吨,每次购买 x 吨,运费为 6 万元/次, 一年的总存储费用为 4x 万元.要使一年的总运费与总存储费用之和最小,则 x 的值是 . 11.(5 分)已知函数 f(x)=x3﹣2x+ex﹣ ,其中 e 是自然对数的底数.若 f (a﹣1)+f(2a2)≤0.则实数 a 的取值范围是 12.(5 分)如图,在同一个平面内,向量 的夹角为 α,且 tanα=7, R),则 m+n= . . ,,的模分别为 1,1, ,与与的夹角为 45°.若 =m +n (m,n∈ 13.(5 分)在平面直角坐标系 xOy 中,A(﹣12,0),B(0,6),点 P 在圆 O: x2+y2=50 上.若 ≤20,则点 P 的横坐标的取值范围是 . 第 2 页(共 37 页) 14.(5 分)设 f(x)是定义在 R 上且周期为 1 的函数,在区间[0,1)上,f(x) =,其中集合 D={x|x= . ,n∈N*},则方程 f(x)﹣lgx=0 的解的个数 是 二.解答题 15.(14 分)如图,在三棱锥 A﹣BCD 中,AB⊥AD,BC⊥BD,平面 ABD⊥平面 BCD,点 E、F(E 与 A、D 不重合)分别在棱 AD,BD 上,且 EF⊥AD. 求证:(1)EF∥平面 ABC; (2)AD⊥AC. 16.(14 分)已知向量 =(cosx,sinx), =(3,﹣ ),x∈[0,π]. 第 3 页(共 37 页) (1)若 ∥ ,求x 的值; (2)记 f(x)= ,求 f(x)的最大值和最小值以及对应的 x 的值. 17.(14 分)如图,在平面直角坐标系 xOy 中,椭圆 E: =1(a>b>0) 的左、右焦点分别为 F1,F2,离心率为 ,两准线之间的距离为8.点 P 在椭圆 E 第 4 页(共 37 页) 上,且位于第一象限,过点 F1 作直线 PF1 的垂线 l1,过点 F2 作直线 PF2 的垂线 l2. (1)求椭圆 E 的标准方程; (2)若直线 l1,l2 的交点 Q 在椭圆 E 上,求点 P 的坐标. 18.(16 分)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ 的高均为 32cm,容器Ⅰ的底面对角线 AC 的长为 10 cm,容器Ⅱ的两底面对角 线 EG,E1G1 的长分别为 14cm 和 62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深 均为 12cm.现有一根玻璃棒 l,其长度为 40cm.(容器厚度、玻璃棒粗细均忽略 第 5 页(共 37 页) 不计) (1)将 l 放在容器Ⅰ中,l 的一端置于点 A 处,另一端置于侧棱 CC1 上,求 l 没 入水中部分的长度; (2)将 l 放在容器Ⅱ中,l 的一端置于点 E 处,另一端置于侧棱 GG1 上,求 l 没 入水中部分的长度. 19 .( 16 分 ) 对 于 给 定 的 正 整 数k , 若 数 列 {an} 满 足 : an﹣k+an﹣k+1+…+an﹣1+an+1+…+an+k﹣1+an+k=2kan 对任意正整数 n(n>k)总成立,则 称数列{an}是“P(k)数列”. (1)证明:等差数列{an}是“P(3)数列”; 第 6 页(共 37 页) (2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数 列. 20.(16 分)已知函数 f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数 f′ (x)的极值点是 f(x)的零点.(极值点是指函数取极值时对应的自变量的值) (1)求 b 关于 a 的函数关系式,并写出定义域; (2)证明:b2>3a; 第 7 页(共 37 页) (3)若 f(x),f′(x)这两个函数的所有极值之和不小于﹣ ,求 a 的取值范 围. 二.非选择题,附加题(21-24 选做题)【选修 4-1:几何证明选讲】(本小题满分 0 分) 21.如图,AB 为半圆 O 的直径,直线 PC 切半圆 O 于点 C,AP⊥PC,P 为垂 足. 求证:(1)∠PAC=∠CAB; 第 8 页(共 37 页) (2)AC2 =AP•AB. [选修 4-2:矩阵与变换] 22.已知矩阵 A= (1)求 AB; ,B= .(2)若曲线 C1: =1 在矩阵 AB 对应的变换作用下得到另一曲线 C2,求 C2 的方程. [选修 4-4:坐标系与参数方程] 23.在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参数), 第 9 页(共 37 页) 曲线 C 的参数方程为 (s 为参数).设 P 为曲线 C 上的动点,求点 P 到 直线 l 的距离的最小值. [选修 4-5:不等式选讲] 24.已知 a,b,c,d 为实数,且 a2+b2=4,c2+d2=16,证明 ac+bd≤8. 第 10 页(共 37 页) 【必做题】 25.如图,在平行六面体 ABCD﹣A1B1C1D1 中,AA1⊥平面 ABCD,且 AB=AD=2,AA1= ,∠BAD=120°. (1)求异面直线 A1B 与 AC1 所成角的余弦值; (2)求二面角 B﹣A1D﹣A 的正弦值. 26.已知一个口袋有 m 个白球,n 个黑球(m,n∈N*,n≥2),这些球除颜色外 全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为 1,2, 3,…,m+n 的抽屉内,其中第 k 次取出的球放入编号为 k 的抽屉(k=1,2, 3,…,m+n). 123…m+n (1)试求编号为 2 的抽屉内放的是黑球的概率 p; 第 11 页(共 37 页) (2)随机变量 x 表示最后一个取出的黑球所在抽屉编号的倒数,E(X)是 X 的 数学期望,证明 E(X)< . 第 12 页(共 37 页) 2017 年江苏省高考数学试卷 参考答案与试题解析 一.填空题 1.(5 分)(2017•江苏)已知集合 A={1,2},B={a,a2+3}.若 A∩B={1},则实 数 a 的值为 1 . 【分析】利用交集定义直接求解. 【解答】解:∵集合 A={1,2},B={a,a2+3}.A∩B={1}, ∴a=1 或 a2+3=1, 解得 a=1. 故答案为:1. 【点评】本题考查实数值的求法,是基础题,解题时要认真审题,注意交集定义 及性质的合理运用. 2.(5 分)(2017•江苏)已知复数 z=(1+i)(1+2i),其中 i 是虚数单位,则 z 的 模是 . 【分析】利用复数的运算法则、模的计算公式即可得出. 【解答】解:复数 z=(1+i)(1+2i)=1﹣2+3i=﹣1+3i, ∴|z|= =.故答案为: .【点评】本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能 力,属于基础题. 3.(5 分)(2017•江苏)某工厂生产甲、乙、丙、丁四种不同型号的产品,产量 分别为 200,400,300,100 件.为检验产品的质量,现用分层抽样的方法从以 上所有的产品中抽取 60 件进行检验,则应从丙种型号的产品中抽取 18 件. 【分析】由题意先求出抽样比例即为 ,再由此比例计算出应从丙种型号的产 第 13 页(共 37 页) 品中抽取的数目. 【解答】解:产品总数为 200+400+300+100=1000 件,而抽取 60 辆进行检验, 抽样比例为 =,则应从丙种型号的产品中抽取 300× 故答案为:18 =18 件, 【点评】本题的考点是分层抽样.分层抽样即要抽样时保证样本的结构和总体的 结构保持一致,按照一定的比例,即样本容量和总体容量的比值,在各层中进行 抽取. 4.(5 分)(2017•江苏)如图是一个算法流程图:若输入 x 的值为 ,则输出y 的值是 ﹣2 . 【分析】直接模拟程序即得结论. 【解答】解:初始值 x= ,不满足 x≥1, 所以 y=2+log2 =2﹣ 故答案为:﹣2. =﹣2, 【点评】本题考查程序框图,模拟程序是解决此类问题的常用方法,注意解题方 法的积累,属于基础题. 第 14 页(共 37 页) 5.(5 分)(2017•江苏)若 tan(α﹣ )= .则 tanα= . 【分析】直接根据两角差的正切公式计算即可 【解答】解:∵tan(α﹣ )= ==∴6tanα﹣6=tanα+1, 解得 tanα= , 故答案为: . 【点评】本题考查了两角差的正切公式,属于基础题 6.(5 分)(2017•江苏)如图,在圆柱 O1O2 内有一个球 O,该球与圆柱的上、 下底面及母线均相切,记圆柱 O1O2 的体积为 V1,球 O 的体积为 V2,则 的值 是 . 【分析】设出球的半径,求出圆柱的体积以及球的体积即可得到结果. 【解答】解:设球的半径为 R,则球的体积为: 圆柱的体积为:πR2•2R=2πR3. R3, 则== . 故答案为: . 【点评】本题考查球的体积以及圆柱的体积的求法,考查空间想象能力以及计算 第 15 页(共 37 页) 能力. 7.(5 分)(2017•江苏)记函数 f(x)= 定义域为 D.在区间[﹣4,5]上 随机取一个数 x,则 x∈D 的概率是 . 【分析】求出函数的定义域,结合几何概型的概率公式进行计算即可. 【解答】解:由 6+x﹣x2≥0 得 x2﹣x﹣6≤0,得﹣2≤x≤3, 则 D=[﹣2,3], 则在区间[﹣4,5]上随机取一个数 x,则 x∈D 的概率 P= = , 故答案为: 【点评】本题主要考查几何概型的概率公式的计算,结合函数的定义域求出 D, 以及利用几何概型的概率公式是解决本题的关键. 8.(5 分)(2017•江苏)在平面直角坐标系 xOy 中,双曲线 ﹣y2=1 的右准线 与它的两条渐近线分别交于点 P,Q,其焦点是 F1,F2,则四边形 F1PF2Q 的面积 是 . 【分析】求出双曲线的准线方程和渐近线方程,得到 P,Q 坐标,求出焦点坐标, 然后求解四边形的面积. 【解答】解:双曲线 ﹣y2=1 的右准线:x= ,双曲线渐近线方程为:y= x, 所以 P( ,),Q( ,﹣ ),F1(﹣2,0).F2(2,0). 则四边形 F1PF2Q 的面积是: 故答案为:2 =2 ..【点评】本题考查双曲线的简单性质的应用,考查计算能力. 9.(5 分)(2017•江苏)等比数列{an}的各项均为实数,其前 n 项为 Sn,已知 S3= ,S6= ,则 a8= 32 . 第 16 页(共 37 页) 【分析】设等比数列{an}的公比为 q≠1,S3= ,S6= ,可得 = , =,联立解出即可得出. 【解答】解:设等比数列{an}的公比为 q≠1, ∵S3= ,S6= ,∴ 解得 a1= ,q=2. = , =,则 a8= =32. 故答案为:32. 【点评】本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能 力,属于中档题. 10.(5 分)(2017•江苏)某公司一年购买某种货物 600 吨,每次购买 x 吨,运 费为 6 万元/次,一年的总存储费用为 4x 万元.要使一年的总运费与总存储费用 之和最小,则 x 的值是 30 . 【分析】由题意可得:一年的总运费与总存储费用之和= +4x,利用基本 不等式的性质即可得出. 【解答】解:由题意可得:一年的总运费与总存储费用之和= +4x≥4×2× =240(万元). 当且仅当 x=30 时取等号. 故答案为:30. 【点评】本题考查了基本不等式的性质及其应用,考查了推理能力与计算能力, 属于基础题. 11.(5 分)(2017•江苏)已知函数 f(x)=x3﹣2x+ex﹣ ,其中 e 是自然对数 的底数.若 f(a﹣1)+f(2a2)≤0.则实数 a 的取值范围是 [﹣1, ] . 第 17 页(共 37 页) 【分析】求出 f(x)的导数,由基本不等式和二次函数的性质,可得 f(x)在 R 上递增;再由奇偶性的定义,可得 f(x)为奇函数,原不等式即为 2a2≤1﹣a, 运用二次不等式的解法即可得到所求范围. 【解答】解:函数 f(x)=x3﹣2x+ex﹣ 的导数为: f′(x)=3×2﹣2+ex+ ≥﹣2+2 =0, 可得 f(x)在 R 上递增; 又 f(﹣x)+f(x)=(﹣x)3+2x+e﹣x﹣ex+x3﹣2x+ex﹣ =0, 可得 f(x)为奇函数, 则 f(a﹣1)+f(2a2)≤0, 即有 f(2a2)≤﹣f(a﹣1)=f(1﹣a), 即有 2a2≤1﹣a, 解得﹣1≤a≤ , 故答案为:[﹣1, ]. 【点评】本题考查函数的单调性和奇偶性的判断和应用,注意运用导数和定义法, 考查转化思想的运用和二次不等式的解法,考查运算能力,属于中档题. 12.(5 分)(2017•江苏)如图,在同一个平面内,向量 1,1, 的夹角为α,且 tanα=7, 的夹角为45°.若 =m +n (m,n∈R),则 m+n= 3 . ,,的模分别为 ,与与【分析】如图所示,建立直角坐标系.A(1,0).由 与的夹角为 α,且 第 18 页(共 37 页) tanα=7.可得 cosα= (α+45°)= .B ,sinα= .C .可得 cos(α+45°)= .sin .利用 =m +n (m,n∈R),即可得出. 【解答】解:如图所示,建立直角坐标系.A(1,0). 的夹角为 α,且 tanα=7. 由与∴cosα= ∴C ,sinα= ..cos(α+45°)= (cosα﹣sinα)= sin(α+45°)= (sinα+cosα)= . .∴B .∵=m +n (m,n∈R), ∴ =m﹣ n, =0+ n, 解得 n= ,m= . 则 m+n=3. 故答案为:3. 【点评】本题考查了向量坐标运算性质、和差公式,考查了推理能力与计算能力, 属于中档题. 13.(5 分)(2017•江苏)在平面直角坐标系 xOy 中,A(﹣12,0),B(0,6), 点 P 在圆 O:x2+y2=50 上.若 ,1] . ≤20,则点 P 的横坐标的取值范围是 [﹣5 第 19 页(共 37 页) 【分析】根据题意,设 P(x0,y0),由数量积的坐标计算公式化简变形可得 2×0+y0+5≤0,分析可得其表示表示直线 2x+y+5≤0 以及直线下方的区域,联立直 线与圆的方程可得交点的横坐标,结合图形分析可得答案. 22【解答】解:根据题意,设 P(x0,y0),则有 x0 +y0 =50, = ( ﹣12﹣x0 , ﹣y0 ) • ( ﹣x0 , 6﹣y0 ) = ( 12+x0 ) x0﹣y0 ( 6﹣y0 ) 22=12×0+6y+x0 +y0 ≤20, 化为:12×0﹣6y0+30≤0, 即 2×0﹣y0+5≤0,表示直线 2x+y+5≤0 以及直线下方的区域, 联立 ,解可得 x0=﹣5 或 x0=1, 结合图形分析可得:点 P 的横坐标 x0 的取值范围是[﹣5 ,1], 故答案为:[﹣5 ,1]. 【点评】本题考查数量积的运算以及直线与圆的位置关系,关键是利用数量积化 简变形得到关于 x0、y0 的关系式. 14.(5 分)(2017•江苏)设 f(x)是定义在 R 上且周期为 1 的函数,在区间[0, 1)上,f(x)= ,其中集合 D={x|x= ,n∈N*},则方程 f(x)﹣lgx=0 的解的个数是 8 . 【分析】由已知中 f(x)是定义在 R 上且周期为 1 的函数,在区间[0,1)上,f 第 20 页(共 37 页) (x)= ,其中集合 D={x|x= ,n∈N*},分析 f(x)的图象与 y=lgx 图象交点的个数,进而可得答案. 【解答】解:∵在区间[0,1)上,f(x)= ,第一段函数上的点的横纵坐标均为有理数, 又 f(x)是定义在 R 上且周期为 1 的函数, ∴在区间[1,2)上,f(x)= ,此时 f(x)的图象与 y=lgx 有且 只有一个交点; 同理: 区间[2,3)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[3,4)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[4,5)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[5,6)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[6,7)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[7,8)上,f(x)的图象与 y=lgx 有且只有一个交点; 区间[8,9)上,f(x)的图象与 y=lgx 有且只有一个交点; 在区间[9,+∞)上,f(x)的图象与 y=lgx 无交点; 故 f(x)的图象与 y=lgx 有 8 个交点; 即方程 f(x)﹣lgx=0 的解的个数是 8, 故答案为:8 【点评】本题考查的知识点是根的存在性及根的个数判断,函数的图象和性质, 转化思想,难度中档. 二.解答题 15.(14 分)(2017•江苏)如图,在三棱锥 A﹣BCD 中,AB⊥AD,BC⊥BD,平 面 ABD⊥平面 BCD,点 E、F(E 与 A、D 不重合)分别在棱 AD,BD 上,且 EF⊥ AD. 第 21 页(共 37 页) 求证:(1)EF∥平面 ABC; (2)AD⊥AC. 【分析】(1)利用 AB∥EF 及线面平行判定定理可得结论; (2)通过取线段 CD 上点 G,连结 FG、EG 使得 FG∥BC,则 EG∥AC,利用线面 垂直的性质定理可知 FG⊥AD,结合线面垂直的判定定理可知 AD⊥平面 EFG,从 而可得结论. 【解答】证明:(1)因为 AB⊥AD,EF⊥AD,且 A、B、E、F 四点共面, 所以 AB∥EF, 又因为 EF⊊平面 ABC,AB⊆平面 ABC, 所以由线面平行判定定理可知:EF∥平面 ABC; (2)在线段 CD 上取点 G,连结 FG、EG 使得 FG∥BC,则 EG∥AC, 因为 BC⊥BD,所以 FG∥BC, 又因为平面 ABD⊥平面 BCD, 所以 FG⊥平面 ABD,所以 FG⊥AD, 又因为 AD⊥EF,且 EF∩FG=F, 所以 AD⊥平面 EFG,所以 AD⊥EG, 故 AD⊥AC. 【点评】本题考查线面平行及线线垂直的判定,考查空间想象能力,考查转化思 想,涉及线面平行判定定理,线面垂直的性质及判定定理,注意解题方法的积累, 属于中档题. 第 22 页(共 37 页) 16.(14 分)(2017•江苏)已知向量 =(cosx,sinx), =(3,﹣ ),x∈[0, π]. (1)若 ∥ ,求x 的值; (2)记 f(x)= ,求 f(x)的最大值和最小值以及对应的 x 的值. 【分析】(1)根据向量的平行即可得到 tanx=﹣ ,问题得以解决, (2)根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出 【解答】解:(1)∵ =(cosx,sinx), =(3,﹣ ), ∥ , ∴﹣ cosx=3sinx, ∴tanx=﹣ ,∵x∈[0,π], ∴x= ,(2)f(x)= =3cosx﹣ sinx=2 (cosx﹣ sinx)=2 cos(x+ ), ∵x∈[0,π], ∴x+ ∈[ , ], ∴﹣1≤cos(x+ )≤ ,当 x=0 时,f(x)有最大值,最大值 3, 当 x= 时,f(x)有最小值,最大值﹣2 .【点评】本题考查了向量的平行和向量的数量积以及三角函数的化简和三角函 数的性质,属于基础题 17.(14 分)(2017•江苏)如图,在平面直角坐标系 xOy 中,椭圆 E: =1 (a>b>0)的左、右焦点分别为 F1,F2,离心率为 ,两准线之间的距离为 8.点 P 在椭圆 E 上,且位于第一象限,过点 F1 作直线 PF1 的垂线 l1,过点 F2 作 第 23 页(共 37 页) 直线 PF2 的垂线 l2. (1)求椭圆 E 的标准方程; (2)若直线 l1,l2 的交点 Q 在椭圆 E 上,求点 P 的坐标. 【分析】(1)由椭圆的离心率公式求得 a=2c,由椭圆的准线方程 x=± ,则 2 ×=8,即可求得 a 和 c 的值,则 b2=a2﹣c2=3,即可求得椭圆方程; (2)设 P 点坐标,分别求得直线 PF2 的斜率及直线 PF1 的斜率,则即可求得 l2 22及 l1 的斜率及方程,联立求得 Q 点坐标,由 Q 在椭圆方程,求得 y0 =x0 ﹣1,联 立即可求得 P 点坐标; 方法二:设 P(m,n),当 m≠1 时, =,=,求得直线 l1 及 l1 的方程,联立求得 Q 点坐标,根据对称性可得 求得 P 点坐标. =±n2,联立椭圆方程,即可 【解答】解:(1)由题意可知:椭圆的离心率 e= = ,则 a=2c,① 椭圆的准线方程 x=± ,由 2× =8,② 由①②解得:a=2,c=1, 则 b2=a2﹣c2=3, ∴椭圆的标准方程: ;(2)方法一:设 P(x0,y0),则直线 PF2 的斜率 =,则直线 l2 的斜率 k2=﹣ ,直线 l2 的方程 y=﹣ (x﹣1), 第 24 页(共 37 页) 直线 PF1 的斜率 =,则直线 l2 的斜率 k2=﹣ ,直线 l2 的方程 y=﹣ (x+1), 联立 ,解得: ,则 Q(﹣x0, ), 由 P,Q 在椭圆上,P,Q 的横坐标互为相反数,纵坐标应相等,则 y0= ,22∴y0 =x0 ﹣1, 则,解得: ,则 ,又 P 在第一象限,所以 P 的坐标为: P( ). ,方法二:设 P(m,n),由 P 在第一象限,则 m>0,n>0, 当 m=1 时, 当 m≠1 时, 不存在,解得:Q 与 F1 重合,不满足题意, =,=,第 25 页(共 37 页) 由 l1⊥PF1,l2⊥PF2,则 =﹣ ,=﹣ ,直线 l1 的方程 y=﹣ (x+1),①直线 l2 的方程 y=﹣ (x﹣1),② 联立解得:x=﹣m,则 Q(﹣m, 由 Q 在椭圆方程,由对称性可得: 即 m2﹣n2=1,或 m2+n2=1, ), =±n2, 由 P(m,n),在椭圆方程, ,解得: ,或 ,无 解, 又 P 在第一象限,所以 P 的坐标为: P( ,). 【点评】本题考查椭圆的标准方程,直线与椭圆的位置关系,考查直线的斜率公 式,考查数形结合思想,考查计算能力,属于中档题. 18.(16 分)(2017•江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台 形玻璃容器Ⅱ的高均为 32cm,容器Ⅰ的底面对角线 AC 的长为 10 cm,容器Ⅱ 的两底面对角线 EG,E1G1 的长分别为 14cm 和 62cm.分别在容器Ⅰ和容器Ⅱ中 注入水,水深均为 12cm.现有一根玻璃棒 l,其长度为 40cm.(容器厚度、玻璃 棒粗细均忽略不计) (1)将 l 放在容器Ⅰ中,l 的一端置于点 A 处,另一端置于侧棱 CC1 上,求 l 没 入水中部分的长度; (2)将 l 放在容器Ⅱ中,l 的一端置于点 E 处,另一端置于侧棱 GG1 上,求 l 没 入水中部分的长度. 第 26 页(共 37 页) 【分析】(1)设玻璃棒在 CC1 上的点为 M,玻璃棒与水面的交点为 N,过 N 作 NP ∥MC,交 AC 于点 P,推导出 CC1 ⊥平面 ABCD,CC1 ⊥AC,NP⊥AC,求出 MC=30cm,推导出△ANP∽△AMC,由此能出玻璃棒 l 没入水中部分的长度. (2)设玻璃棒在 GG1 上的点为 M,玻璃棒与水面的交点为 N,过点 N 作 NP⊥ EG,交 EG 于点 P,过点 E 作 EQ⊥E1G1,交 E1G1 于点 Q,推导出 EE1G1G 为等腰 梯形,求出 E1Q=24cm,E1E=40cm,由正弦定理求出 sin∠GEM= ,由此能求出 玻璃棒 l 没入水中部分的长度. 【解答】解:(1)设玻璃棒在 CC1 上的点为 M,玻璃棒与水面的交点为 N, 在平面 ACM 中,过 N 作 NP∥MC,交 AC 于点 P, ∵ABCD﹣A1B1C1D1 为正四棱柱,∴CC1⊥平面 ABCD, 又∵AC⊂平面 ABCD,∴CC1⊥AC,∴NP⊥AC, ∴NP=12cm,且 AM2=AC2+MC2,解得 MC=30cm, ∵NP∥MC,∴△ANP∽△AMC, ∴=,,得 AN=16cm. ∴玻璃棒 l 没入水中部分的长度为 16cm. (2)设玻璃棒在 GG1 上的点为 M,玻璃棒与水面的交点为 N, 在平面 E1EGG1 中,过点 N 作 NP⊥EG,交 EG 于点 P, 过点 E 作 EQ⊥E1G1,交 E1G1 于点 Q, ∵EFGH﹣E1F1G1H1 为正四棱台,∴EE1=GG1,EG∥E1G1, EG≠E1G1, ∴EE1G1G 为等腰梯形,画出平面 E1EGG1 的平面图, ∵E1G1=62cm,EG=14cm,EQ=32cm,NP=12cm, 第 27 页(共 37 页) ∴E1Q=24cm, 由勾股定理得:E1E=40cm, ∴sin∠EE1G1= ,sin∠EGM=sin∠EE1G1= ,cos ,根据正弦定理得: =,∴sin ,cos ,∴sin∠GEM=sin(∠EGM+∠EMG)=sin∠EGMcos∠EMG+cos∠EGMsin∠EMG= , ∴EN= =20cm. =∴玻璃棒 l 没入水中部分的长度为 20cm. 【点评】本题考查玻璃棒 l 没入水中部分的长度的求法,考查空间中线线、线面、 面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能 力,考查数形结合思想、化归与转化思想,是中档题. 19 .( 16 分 )( 2017• 江 苏 ) 对 于 给 定 的 正 整 数k , 若 数 列 {an} 满 足 : an﹣k+an﹣k+1+…+an﹣1+an+1+…+an+k﹣1+an+k=2kan 对任意正整数 n(n>k)总成立,则 称数列{an}是“P(k)数列”. (1)证明:等差数列{an}是“P(3)数列”; (2)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数 第 28 页(共 37 页) 列. 【分析】(1)由题意可知根据等差数列的性质,an﹣3+an﹣2+an﹣1+an+1+an+2+an+3 =(an﹣3+an+3)+(an﹣2+an+2)+(an﹣1+an+1)═2×3an,根据“P(k)数列”的定义, 可得数列{an}是“P(3)数列”; ( 2 ) 由 “P ( k ) 数 列 ” 的 定 义 , 则an﹣2+an﹣1+an+1+an+2=4an , an﹣3+an﹣2+an﹣1+an+1+an+2+an+3=6an,变形整理即可求得 2an=an﹣1+an+1,即可证明 数列{an}是等差数列. 【解答】解:(1)证明:设等差数列{an}首项为 a1,公差为 d,则 an=a1+(n﹣1) d, 则 an﹣3+an﹣2+an﹣1+an+1+an+2+an+3, =(an﹣3+an+3)+(an﹣2+an+2)+(an﹣1+an+1), =2an+2an+2an, =2×3an, ∴等差数列{an}是“P(3)数列”; (2)证明:由数列{an}是“P(2)数列”则 an﹣2+an﹣1+an+1+an+2=4an,① 数列{an}是“P(3)数列”an﹣3+an﹣2+an﹣1+an+1+an+2+an+3=6an,② 由①可知:an﹣3+an﹣2+an+an+1=4an﹣1,③ an﹣1+an+an+2+an+3=4an+1,④ 由②﹣(③+④):﹣2an=6an﹣4an﹣1﹣4an+1, 整理得:2an=an﹣1+an+1, ∴数列{an}是等差数列. 【点评】本题考查等差数列的性质,考查数列的新定义的性质,考查数列的运算, 考查转化思想,属于中档题. 20.(16 分)(2017•江苏)已知函数 f(x)=x3+ax2+bx+1(a>0,b∈R)有极值, 第 29 页(共 37 页) 且导函数 f′(x)的极值点是 f(x)的零点.(极值点是指函数取极值时对应的自 变量的值) (1)求 b 关于 a 的函数关系式,并写出定义域; (2)证明:b2>3a; (3)若 f(x),f′(x)这两个函数的所有极值之和不小于﹣ ,求 a 的取值范 围. 【分析】(1)通过对 f(x)=x3+ax2+bx+1 求导可知 g(x)=f′(x)=3×2+2ax+b,进 而再求导可知 g′(x)=6x+2a,通过令 g′(x)=0 进而可知 f′(x)的极小值点为 x=﹣ ,从而 f(﹣ )=0,整理可知 b= (a>0,b∈R)有极值可知 f′(x)=0 有两个不等的实根,进而可知 a>3. (2 )通过(1 )构造函数 h (a )=b2﹣3a= (4a3﹣27 ) + (a>0),结合 f(x)=x3+ax2+bx+1 ﹣+=(a3﹣27),结合 a>3 可知 h(a)>0,从而可得结论; (3)通过(1)可知 f′(x)的极小值为 f′(﹣ )=b﹣ ,利用韦达定理及完 全平方关系可知 y=f(x)的两个极值之和为 +2,进而问题转化为解不 等式 b﹣ +2= ﹣ ≥﹣ ,因式分解即得结论. ﹣+﹣【解答】(1)解:因为 f(x)=x3+ax2+bx+1, 所以 g(x)=f′(x)=3×2+2ax+b,g′(x)=6x+2a, 令 g′(x)=0,解得 x=﹣ . 由于当 x>﹣ 时 g′(x)>0,g(x)=f′(x)单调递增;当 x<﹣ 时 g′(x)< 0,g(x)=f′(x)单调递减; 所以 f′(x)的极小值点为 x=﹣ , 由于导函数 f′(x)的极值点是原函数 f(x)的零点, 所以 f(﹣ )=0,即﹣ 所以 b= + (a>0). +﹣+1=0, 因为 f(x)=x3+ax2+bx+1(a>0,b∈R)有极值, 第 30 页(共 37 页) 所以 f′(x)=3×2+2ax+b=0 有两个不等的实根, 所以 4a2﹣12b>0,即 a2﹣ + >0,解得 a>3, 所以 b= + (a>3). (2 )证明:由(1 )可知 h (a )=b2﹣3a= ﹣+=(4a3﹣27 ) (a3﹣27), 由于 a>3,所以 h(a)>0,即 b2>3a; (3)解:由(1)可知 f′(x)的极小值为 f′(﹣ )=b﹣ 设 x1,x2 是 y=f(x)的两个极值点,则 x1+x2= 所以 f(x1)+f(x2)= +a( )+b(x1+x2)+2 =(x1+x2)[(x1+x2)2﹣3x1x2]+a[(x1+x2)2﹣2x1x2]+b(x1+x2)+2 +2, 又因为 f(x),f′(x)这两个函数的所有极值之和不小于﹣ , 所以 b﹣ +2= ﹣ ≥﹣ , ,,x1x2= , ++=﹣+﹣因为 a>3,所以 2a3﹣63a﹣54≤0, 所以 2a(a2﹣36)+9(a﹣6)≤0, 所以(a﹣6)(2a2+12a+9)≤0, 由于 a>3 时 2a2+12a+9>0, 所以 a﹣6≤0,解得 a≤6, 所以 a 的取值范围是(3,6]. 【点评】本题考查利用导数研究函数的单调性、极值,考查运算求解能力,考查 转化思想,注意解题方法的积累,属于难题. 二.非选择题,附加题(21-24 选做题)【选修 4-1:几何证明选讲】(本小题满分 0 分) 第 31 页(共 37 页) 21.(2017•江苏)如图,AB 为半圆 O 的直径,直线 PC 切半圆 O 于点 C,AP⊥ PC,P 为垂足. 求证:(1)∠PAC=∠CAB; (2)AC2 =AP•AB. 【分析】(1)利用弦切角定理可得:∠ACP=∠ABC.利用圆的性质可得∠ ACB=90°.再利用三角形内角和定理即可证明. (2)由(1)可得:△APC∽△ACB,即可证明. 【解答】证明:(1)∵直线 PC 切半圆 O 于点 C,∴∠ACP=∠ABC. ∵AB 为半圆 O 的直径,∴∠ACB=90°. ∵AP⊥PC,∴∠APC=90°. ∴∠PAC=90°﹣∠ACP,∠CAB=90°﹣∠ABC, ∴∠PAC=∠CAB. (2)由(1)可得:△APC∽△ACB, ∴=.∴AC2 =AP•AB. 【点评】本题考查了弦切角定理、圆的性质、三角形内角和定理、三角形相似的 判定与性质定理,考查了推理能力与计算能力,属于中档题. [选修 4-2:矩阵与变换] 22.(2017•江苏)已知矩阵 A= (1)求 AB; ,B= .第 32 页(共 37 页) (2)若曲线 C1: =1 在矩阵 AB 对应的变换作用下得到另一曲线 C2,求 C2 的方程. 【分析】(1)按矩阵乘法规律计算; (2)求出变换前后的坐标变换规律,代入曲线 C1 的方程化简即可. 【解答】解:(1)AB= =,(2)设点 P(x,y)为曲线 C1 的任意一点, 点 P 在矩阵 AB 的变换下得到点 P′(x0,y0), 则=,即 x0=2y,y0=x, ∴x=y0,y= ,22∴,即 x0 +y0 =8, ∴曲线 C2 的方程为 x2+y2=8. 【点评】本题考查了矩阵乘法与矩阵变换,属于中档题. [选修 4-4:坐标系与参数方程] 23.(2017•江苏)在平面直角坐标系 xOy 中,已知直线 l 的参数方程为 (t 为参数),曲线 C 的参数方程为 (s 为参数).设 P 为曲线 C 上的动 点,求点 P 到直线 l 的距离的最小值. 【分析】求出直线 l 的直角坐标方程,代入距离公式化简得出距离 d 关于参数 s 的函数,从而得出最短距离. 【解答】解:直线 l 的直角坐标方程为 x﹣2y+8=0, ∴P 到直线 l 的距离 d= =,∴当 s= 时,d 取得最小值 =.【点评】本题考查了参数方程的应用,属于基础题. 第 33 页(共 37 页) [选修 4-5:不等式选讲] 24.(2017•江苏)已知 a,b,c,d 为实数,且 a2+b2=4,c2+d2=16,证明 ac+bd≤ 8. 【分析】a2+b2=4,c2+d2=16,令 a=2cosα,b=2sinα,c=4cosβ,d=4sinβ.代入 ac+bd 2化简,利用三角函数的单调性即可证明.另解:由柯西不等式可得:(ac+bd)≤ (a2+b2)(c2+d2),即可得出. 【解答】证明:∵a2+b2=4,c2+d2=16, 令 a=2cosα,b=2sinα,c=4cosβ,d=4sinβ. ∴ac+bd=8(cosαcosβ+sinαsinβ)=8cos(α﹣β)≤8.当且仅当 cos(α﹣β)=1 时 取等号. 因此 ac+bd≤8. 另解:由柯西不等式可得:(ac+bd)2≤(a2+b2)(c2+d2)=4×16=64,当且仅当 时取等号. ∴﹣8≤ac+bd≤8. 【点评】本题考查了对和差公式、三角函数的单调性、不等式的性质,考查了推 理能力与计算能力,属于中档题. 【必做题】 25.(2017•江苏)如图,在平行六面体 ABCD﹣A1B1C1D1 中,AA1⊥平面 ABCD, 且 AB=AD=2,AA1= ,∠BAD=120°. (1)求异面直线 A1B 与 AC1 所成角的余弦值; (2)求二面角 B﹣A1D﹣A 的正弦值. 【分析】在平面 ABCD 内,过 A 作 Ax⊥AD,由 AA1⊥平面 ABCD,可得 AA1⊥Ax, 第 34 页(共 37 页) AA1⊥AD,以 A 为坐标原点,分别以 Ax、AD、AA1 所在直线为 x、y、z 轴建立空 间直角坐标系.结合已知求出 A,B,C,D,A1,C1 的坐标,进一步求出 ,,,的坐标. (1)直接利用两法向量所成角的余弦值可得异面直线 A1B 与 AC1 所成角的余弦 值; (2)求出平面 BA1D 与平面 A1AD 的一个法向量,再由两法向量所成角的余弦值 求得二面角 B﹣A1D﹣A 的余弦值,进一步得到正弦值. 【解答】解:在平面 ABCD 内,过 A 作 Ax⊥AD, ∵AA1⊥平面 ABCD,AD、Ax⊂平面 ABCD, ∴AA1⊥Ax,AA1⊥AD, 以 A 为坐标原点,分别以 Ax、AD、AA1 所在直线为 x、y、z 轴建立空间直角坐标 系. ∵AB=AD=2,AA1= ,∠BAD=120°, ∴A(0,0,0),B( D(0,2,0), A1(0,0, ),C1( = ( ),C( ,1,0), ). ), = ( ), ,.(1)∵cos< >= =.∴异面直线 A1B 与 AC1 所成角的余弦值为 ; (2)设平面 BA1D 的一个法向量为 ,由,得 ,取 x= ,得 ;取平面 A1AD 的一个法向量为 .第 35 页(共 37 页) ∴cos< >= =.∴ 二 面 角B﹣A1D﹣A 的 正 弦 值 为, 则 二 面 角B﹣A1D﹣A 的 正 弦 值 为 .【点评】本题考查异面直线所成的角与二面角,训练了利用空间向量求空间角, 是中档题. 26.(2017•江苏)已知一个口袋有 m 个白球,n 个黑球(m,n∈N*,n≥2),这 些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编 号为 1,2,3,…,m+n 的抽屉内,其中第 k 次取出的球放入编号为 k 的抽屉 (k=1,2,3,…,m+n). 123…m+n (1)试求编号为 2 的抽屉内放的是黑球的概率 p; (2)随机变量 x 表示最后一个取出的黑球所在抽屉编号的倒数,E(X)是 X 的 数学期望,证明 E(X)< .【分析】(1)设事件 Ai 表示编号为 i 的抽屉里放的是黑球,则 p=p(A2)=P (A2|A1)P(A1)+P(A2| )P( ),由此能求出编号为2 的抽屉内放的是黑 球的概率. (2)X 的所有可能取值为 ,…, ,P(x= )= ,k=n,n+1, n+2,…,n+m,从而 E(X)= ()= ,由此能证明 E 第 36 页(共 37 页) (X)< .【解答】解:(1)设事件 Ai 表示编号为 i 的抽屉里放的是黑球, 则 p=p(A2)=P(A2|A1)P(A1)+P(A2| )P( )===.证明:(2)∵X 的所有可能取值为 ,…, ,P(x= )= ∴E(X)= ,k=n,n+1,n+2,…,n+m, ()= ==<=•( )==,∴E(X)< .【点评】本题考查概率的求法,考查离散型随机变量的分布列、数学期望等基础 知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、 化归与转化思想,是中档题. 第 37 页(共 37 页)
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





