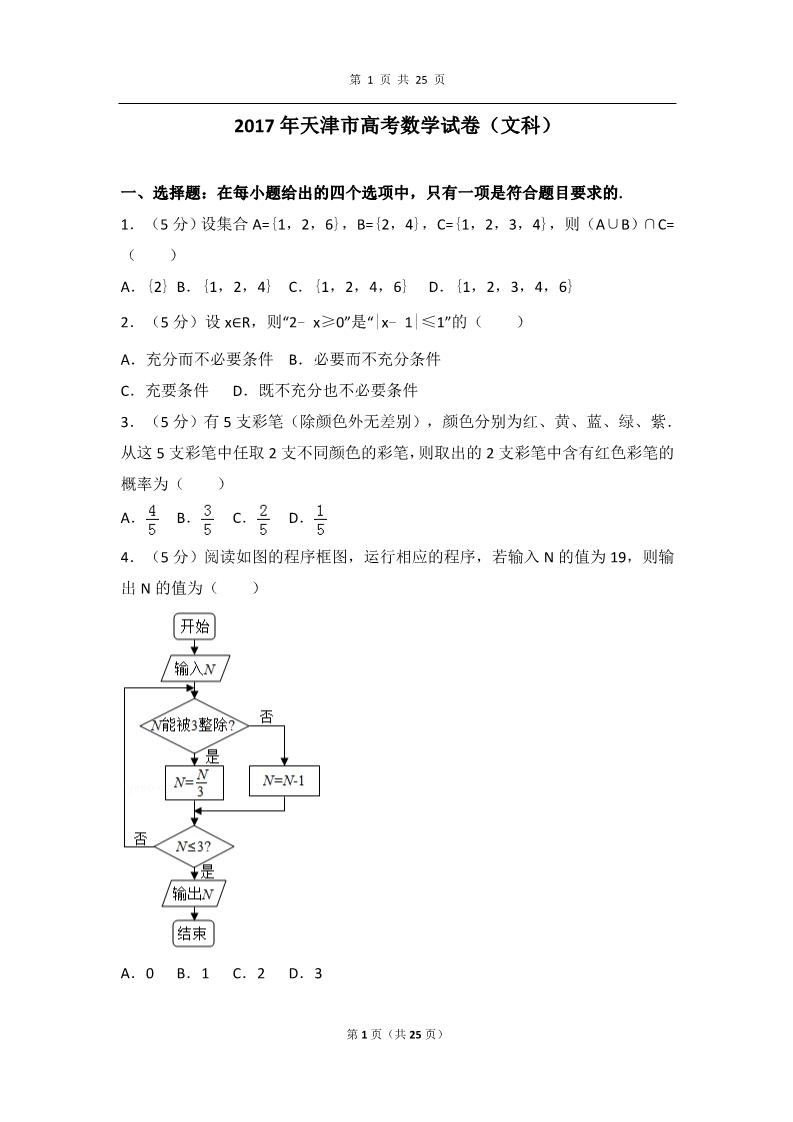
第 1 页 共 25 页 2017 年天津市高考数学试卷（文科） 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. 1．（5 分）设集合 A={1，2，6}，B={2，4}，C={1，2，3，4}，则（A∪B）∩C= （ ） A．{2} B．{1，2，4} C．{1，2，4，6} D．{1，2，3，4，6} 2．（5 分）设 x∈R，则“2﹣x≥0”是“|x﹣1|≤1”的（ ） A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 3．（5 分）有 5 支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫． 从这 5 支彩笔中任取 2 支不同颜色的彩笔，则取出的 2 支彩笔中含有红色彩笔的 概率为（ ） A． B． C． D． 4．（5 分）阅读如图的程序框图，运行相应的程序，若输入 N 的值为 19，则输 出 N 的值为（ ） A．0 B．1 C．2 D．3 第 1 页（共 25 页） 第 2 页 共 25 页 5．（5 分）已知双曲线 ﹣=1（a＞0，b＞0）的右焦点为 F，点 A 在双曲线 的渐近线上，△OAF 是边长为 2 的等边三角形（O 为原点），则双曲线的方程为（ ）A． B． C． D． 6．（5 分）已知奇函数 f（x）在 R 上是增函数．若 a=﹣f（ ），b=f（ log24.1），c=f（20.8），则 a，b，c 的大小关系为（ ） A．a＜b＜c B．b＜a＜c C．c＜b＜a D．c＜a＜b 7．（5 分）设函数 f（x）=2sin（ωx+φ），x∈R，其中 ω＞0，|φ|＜π．若 f（ ）=2，f（ ）=0，且 f（x）的最小正周期大于 2π，则（ ） A．ω= ，φ= C．ω= ，φ=﹣ B．ω= ，φ=﹣ D．ω= ，φ= 8．（5 分）已知函数 f（x）= ，设 a∈R，若关于 x 的不等式 f（x）≥ | +a|在 R 上恒成立，则 a 的取值范围是（ ） A．[﹣2，2] B． C． D． 二、填空题：本大题共 6 小题，每小题 5 分，共 30 分. 9．（5 分）已知 a∈R，i 为虚数单位，若 为实数，则a 的值为 ． 10．（5 分）已知 a∈R，设函数 f（x）=ax﹣lnx 的图象在点（1，f（1））处的切 线为 l，则 l 在 y 轴上的截距为 11．（5 分）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积 为 18，则这个球的体积为 ． 12．（5 分）设抛物线 y2=4x 的焦点为 F，准线为 l．已知点 C 在 l 上，以 C 为圆 ． 心的圆与 y 轴的正半轴相切于点 A．若∠FAC=120°，则圆的方程为 ． 第 2 页（共 25 页） 第 3 页 共 25 页 13．（5 分）若 a，b∈R，ab＞0，则 的最小值为 ． 14．（5 分）在△ABC 中，∠A=60°，AB=3，AC=2．若 =2 ，=λ ﹣（λ∈ R），且 =﹣4，则 λ 的值为 ． 三、解答题：本大题共 6 小题，共 80 分．解答应写出文字说明，证明过程或演 算步骤． 15．（13 分）在△ABC 中，内角 A，B，C 所对的边分别为 a，b，c．已知 asinA=4bsinB ，ac= （a2﹣b2﹣c2）． （Ⅰ）求 cosA 的值； （Ⅱ）求 sin（2B﹣A）的值． 16．（13 分）电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广 告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视 人次如下表所示： 连续剧播放时长（分钟） 广告播放时长（分钟） 收视人次（万） 70 60 5560 25 甲乙已知电视台每周安排的甲、乙连续剧的总播放时间不多于 600 分钟，广告的总播 放时间不少于 30 分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的 2 倍． 分别用 x，y 表示每周计划播出的甲、乙两套连续剧的次数． （I）用 x，y 列出满足题目条件的数学关系式，并画出相应的平面区域； （II）问电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？ 17．（13 分）如图，在四棱锥 P﹣ABCD 中，AD⊥平面 PDC，AD∥BC，PD⊥PB， AD=1，BC=3，CD=4，PD=2． （Ⅰ）求异面直线 AP 与 BC 所成角的余弦值； （Ⅱ）求证：PD⊥平面 PBC； （Ⅲ）求直线 AB 与平面 PBC 所成角的正弦值． 第 3 页（共 25 页） 第 4 页 共 25 页 18．（13 分）已知{an}为等差数列，前 n 项和为 Sn（n∈N*），{bn}是首项为 2 的等比数列，且公比大于 0，b2+b3=12，b3=a4﹣2a1，S11=11b4． （Ⅰ）求{an}和{bn}的通项公式； （Ⅱ）求数列{a2nbn}的前 n 项和（n∈N*）． 19．（14 分）设 a，b∈R，|a|≤1．已知函数 f（x）=x3﹣6×2﹣3a（a﹣4）x+b， g（x）=exf（x）． （Ⅰ）求 f（x）的单调区间； （Ⅱ）已知函数 y=g（x）和 y=ex 的图象在公共点（x0，y0）处有相同的切线， （i）求证：f（x）在 x=x0 处的导数等于 0； （ii）若关于 x 的不等式 g（x）≤ex 在区间[x0﹣1，x0+1]上恒成立，求 b 的取值 范围． 20．（14 分）已知椭圆 +=1（a＞b＞0）的左焦点为 F（﹣c，0），右顶点 为 A，点 E 的坐标为（0，c），△EFA 的面积为 （I）求椭圆的离心率； ．（II）设点 Q 在线段 AE 上，|FQ|= c，延长线段 FQ 与椭圆交于点 P，点 M，N 在 x 轴上，PM∥QN，且直线 PM 与直线 QN 间的距离为 c，四边形 PQNM 的面 积为 3c． （i）求直线 FP 的斜率； （ii）求椭圆的方程． 第 4 页（共 25 页） 第 5 页 共 25 页 2017 年天津市高考数学试卷（文科） 参考答案与试题解析 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. 1．（5 分）（2017•天津）设集合 A={1，2，6}，B={2，4}，C={1，2，3，4}， 则（A∪B）∩C=（ ） A．{2} B．{1，2，4} C．{1，2，4，6} D．{1，2，3，4，6} 【分析】由并集定义先求出 A∪B，再由交集定义能求出（A∪B）∩C． 【解答】解：∵集合 A={1，2，6}，B={2，4}，C={1，2，3，4}， ∴（A∪B）∩C={1，2，4，6}∩{1，2，3，4}={1，2，4}． 故选：B． 【点评】本题考查并集和交集的求法，是基础题，解题时要认真审题，注意交集 和交集定义的合理运用． 2．（5 分）（2017•天津）设 x∈R，则“2﹣x≥0”是“|x﹣1|≤1”的（ ） A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 【分析】求出不等式的等价条件，结合充分条件和必要条件的定义进行判断即可 ．【解答】解：由 2﹣x≥0 得 x≤2， 由|x﹣1|≤1 得﹣1≤x﹣1≤1， 得 0≤x≤2． 则“2﹣x≥0”是“|x﹣1|≤1”的必要不充分条件， 故选：B 【点评】本题主要考查充分条件和必要条件的判断，结合充分条件和必要条件的 定义以及不等式的性质是解决本题的关键． 第 5 页（共 25 页） 第 6 页 共 25 页 3．（5 分）（2017•天津）有 5 支彩笔（除颜色外无差别），颜色分别为红、黄 、蓝、绿、紫．从这 5 支彩笔中任取 2 支不同颜色的彩笔，则取出的 2 支彩笔中 含有红色彩笔的概率为（ ） A． B． C． D． 【分析】先求出基本事件总数 n= =10，再求出取出的 2 支彩笔中含有红色彩笔 包含的基本事件个数 m= =4，由此能求出取出的 2 支彩笔中含有红色彩笔的 概率． 【解答】解：有 5 支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫 ，从这 5 支彩笔中任取 2 支不同颜色的彩笔， 基本事件总数 n= =10， 取出的 2 支彩笔中含有红色彩笔包含的基本事件个数 m= =4， ∴取出的 2 支彩笔中含有红色彩笔的概率为 p= = 故选：C． ．【点评】本小题主要考查概率、古典概型、排列组合等基础知识，考查运算求解 能力和推理论证能力，是基础题． 4．（5 分）（2017•天津）阅读如图的程序框图，运行相应的程序，若输入 N 的 值为 19，则输出 N 的值为（ ） 第 6 页（共 25 页） 第 7 页 共 25 页 A．0 B．1 C．2 D．3 【分析】根据程序框图，进行模拟计算即可． 【解答】解：第一次 N=19，不能被 3 整除，N=19﹣1=18≤3 不成立， 第二次 N=18，18 能被 3 整除，N= =6，N=6≤3 不成立， 第三次 N=6，能被 3 整除，N═ =2≤3 成立， 输出 N=2， 故选：C 【点评】本题主要考查程序框图的识别和应用，根据条件进行模拟计算是解决本 题的关键． 5．（5 分）（2017•天津）已知双曲线 ﹣=1（a＞0，b＞0）的右焦点为 F， 点 A 在双曲线的渐近线上，△OAF 是边长为 2 的等边三角形（O 为原点），则双 曲线的方程为（ ） A． B． C． D． 【分析】利用三角形是正三角形，推出 a，b 关系，通过 c=2，求解 a，b，然后 第 7 页（共 25 页） 第 8 页 共 25 页 等到双曲线的方程． 【解答】解：双曲线 ﹣=1（a＞0，b＞0）的右焦点为 F，点 A 在双曲线的 渐近线上，△OAF 是边长为 2 的等边三角形（O 为原点）， 可得 c=2， ，即 ，，解得 a=1，b= ，双曲线的焦点坐标在 x 轴，所得双曲线方程为： ．故选：D． 【点评】本题考查双曲线的简单性质的应用，考查计算能力． 6．（5 分）（2017•天津）已知奇函数 f（x）在 R 上是增函数．若 a=﹣f（ ），b=f（log24.1），c=f（20.8），则 a，b，c 的大小关系为（ ） A．a＜b＜c B．b＜a＜c C．c＜b＜a D．c＜a＜b 【分析】根据奇函数 f（x）在 R 上是增函数，化简 a、b、c，即可得出 a，b，c 的大小． 【解答】解：奇函数 f（x）在 R 上是增函数， ∴a=﹣f（ ）=f（log25）， b=f（log24.1）， c=f（20.8）， 又 1＜20.8＜2＜log24.1＜log25， ∴f（20.8）＜f（log24.1）＜f（log25）， 即 c＜b＜a． 故选：C． 【点评】本题考查了函数的奇偶性与单调性的应用问题，是基础题． 7．（5 分）（2017•天津）设函数 f（x）=2sin（ωx+φ），x∈R，其中 ω＞0，|φ| ＜π．若 f（ ）=2，f（ ）=0，且 f（x）的最小正周期大于 2π，则（ ） 第 8 页（共 25 页） 第 9 页 共 25 页 A．ω= ，φ= B．ω= ，φ=﹣ D．ω= ，φ= C．ω= ，φ=﹣ 【分析】由题意求得 ，再由周期公式求得ω，最后由若 f（ 【解答】解：由 f（x）的最小正周期大于 2π，得 ）=2 求得 φ 值． ，又 f（ ）=2，f（ ）=0，得 ，∴T=3π，则 ，即 ．∴f（x）=2sin（ωx+φ）=2sin（ x+φ）， 由 f（ ∴φ+ ）= ，得 sin（φ+ ）=1． =，k∈Z． 取 k=0，得 φ= ＜π． ，φ= 故选：A． ∴．【点评】本题考查由三角函数的部分图象求解析式，考查 y=Asin（ωx+φ）型函 数的性质，是中档题． 8．（5 分）（2017•天津）已知函数 f（x）= 的不等式 f（x）≥| +a|在 R 上恒成立，则 a 的取值范围是（ ） A．[﹣2，2] B． C． D． ，设 a∈R，若关于 x 【分析】根据题意，作出函数 f（x）的图象，令 g（x）=| +a|，分析 g（x）的 图象特点，将不等式 f（x）≥| +a|在 R 上恒成立转化为函数 f（x）的图象在 g（ x）上的上方或相交的问题，分析可得 f（0）≥g（0），即 2≥|a|，解可得 a 的 取值范围，即可得答案． 第 9 页（共 25 页） 第 10 页 共 25 页 【解答】解：根据题意，函数 f（x）= 的图象如图： 令 g（x）=| +a|，其图象与 x 轴相交与点（﹣2a，0）， 在区间（﹣∞，﹣2a）上为减函数，在（﹣2a，+∞）为增函数， 若不等式 f（x）≥| +a|在 R 上恒成立，则函数 f（x）的图象在 g（x）上的上方或相交， 则必有 f（0）≥g（0）， 即 2≥|a|， 解可得﹣2≤a≤2， 故选：A． 【点评】本题考查分段函数的应用，关键是作出函数 f（x）的图象，将函数的恒 成立问题转化为图象的上下位置关系． 二、填空题：本大题共 6 小题，每小题 5 分，共 30 分. 9．（5 分）（2017•天津）已知 a∈R，i 为虚数单位，若 为实数，则 a 的值为 ﹣2 ． 【分析】运用复数的除法法则，结合共轭复数，化简 ，再由复数为实数的条 件：虚部为 0，解方程即可得到所求值． 【解答】解：a∈R，i 为虚数单位， 第 10 页（共 25 页） 第 11 页 共 25 页 ===﹣i由为实数， 可得﹣ =0， 解得 a=﹣2． 故答案为：﹣2． 【点评】本题考查复数的乘除运算，注意运用共轭复数，同时考查复数为实数的 条件：虚部为 0，考查运算能力，属于基础题． 10．（5 分）（2017•天津）已知 a∈R，设函数 f（x）=ax﹣lnx 的图象在点（1，f （1））处的切线为 l，则 l 在 y 轴上的截距为 1 ． 【分析】求出函数的导数，然后求解切线斜率，求出切点坐标，然后求解切线方 程，推出 l 在 y 轴上的截距． 【解答】解：函数 f（x）=ax﹣lnx，可得 f′（x）=a﹣ ，切线的斜率为：k=f′（1） =a﹣1， 切点坐标（1，a），切线方程 l 为：y﹣a=（a﹣1）（x﹣1）， l 在 y 轴上的截距为：a+（a﹣1）（﹣1）=1． 故答案为：1． 【点评】本题考查曲线的切线方程的求法，考查转化思想以及计算能力． 11．（5 分）（2017•天津）已知一个正方体的所有顶点在一个球面上，若这个 正方体的表面积为 18，则这个球的体积为 ． 【分析】根据正方体和球的关系，得到正方体的体对角线等于直径，结合球的体 积公式进行计算即可． 【解答】解：设正方体的棱长为 a， ∵这个正方体的表面积为 18， ∴6a2=18， 第 11 页（共 25 页） 第 12 页 共 25 页 则 a2=3，即 a= ，∵一个正方体的所有顶点在一个球面上， ∴正方体的体对角线等于球的直径， 即a=2R， 即 R= ， 则球的体积 V= π•（ ）3= ；故答案为： ．【点评】本题主要考查空间正方体和球的关系，利用正方体的体对角线等于直径 ，结合球的体积公式是解决本题的关键． 12．（5 分）（2017•天津）设抛物线 y2=4x 的焦点为 F，准线为 l．已知点 C 在 l 上，以 C 为圆心的圆与 y 轴的正半轴相切于点 A．若∠FAC=120°，则圆的方程为 （x+1）2+ =1 ． 【分析】根据题意可得 F（﹣1，0），∠FAO=30°，OA= =1，由此求得 OA 的值，可得圆心 C 的坐标以及圆的半径，从而求得圆 C 方程． 【解答】解：设抛物线 y2=4x 的焦点为 F（1，0），准线 l：x=﹣1，∵点 C 在 l 上，以 C 为圆心的圆与 y 轴的正半轴相切与点 A， ∵∠FAC=120°，∴∠FAO=30°，∴OA= ==1，∴OA= ，∴A（0， ），如图所示： ∴ C （ ﹣1 ， ） ， 圆 的 半 径 为CA=1 ， 故 要 求 的 圆 的 标 准 方 程 为 ，故答案为：（x+1）2+ =1． 第 12 页（共 25 页） 第 13 页 共 25 页 【点评】本题主要考查求圆的标准方程的方法，抛物线的简单几何性质，属于中 档题． 13．（5 分）（2017•天津）若 a，b∈R，ab＞0，则 的最小值为 4 ． 【分析】【方法一】两次利用基本不等式，即可求出最小值，需要注意不等式等 号成立的条件是什么． 【方法二】将 拆成 +，利用柯西不等式求出最小值． 【解答】解：【解法一】a，b∈R，ab＞0， ∴≥==4ab+ ≥2 =4， 当且仅当 即，，即 a= ，b= 或 a=﹣ ，b=﹣ 时取“=”； ∴上式的最小值为 4． 第 13 页（共 25 页） 第 14 页 共 25 页 【解法二】a，b∈R，ab＞0， ∴=+++≥4 =4， 当且仅当 ，即，即 a= ，b= 或 a=﹣ ，b=﹣ 时取“=”； ∴上式的最小值为 4． 故答案为：4． 【点评】本题考查了基本不等式的应用问题，是中档题． 14．（5 分）（2017•天津）在△ABC 中，∠A=60°，AB=3，AC=2．若 =2 =λ （λ∈R），且 =﹣4，则 λ 的值为 ． 【分析】根据题意画出图形，结合图形，利用 表示出 列出方程求出 λ 的值． ，﹣、，再根据平面向量的数量积 【解答】解：如图所示， △ABC 中，∠A=60°，AB=3，AC=2， =2 ，∴=+=+==+ （ ﹣）+，又=λ ﹣（λ∈R）， 第 14 页（共 25 页） 第 15 页 共 25 页 ∴=（ =（ λ﹣ ） =（ λ﹣ ）×3×2×cos60°﹣ ×32+ λ×22=﹣4， λ=1， 解得 λ= 故答案为： +）•（λ ﹣）•﹣ + λ ∴．．【点评】本题考查了平面向量的线性运算与数量积运算问题，是中档题． 三、解答题：本大题共 6 小题，共 80 分．解答应写出文字说明，证明过程或演 算步骤． 15．（13 分）（2017•天津）在△ABC 中，内角 A，B，C 所对的边分别为 a，b， c．已知 asinA=4bsinB，ac= （a2﹣b2﹣c2）． （Ⅰ）求 cosA 的值； （Ⅱ）求 sin（2B﹣A）的值． 【分析】（Ⅰ）由正弦定理得 asinB=bsinA，结合 asinA=4bsinB，得 a=2b．再由 ，得 ，代入余弦定理的推论可求 cosA 的 值； （Ⅱ）由（Ⅰ）可得 ，代入 asinA=4bsinB，得 sinB，进一步求得 cosB． 利用倍角公式求 sin2B，cos2B，展开两角差的正弦可得 sin（2B﹣A）的值． 【解答】（Ⅰ）解：由 ，得 asinB=bsinA， 又 asinA=4bsinB，得 4bsinB=asinA， 第 15 页（共 25 页） 第 16 页 共 25 页 两式作比得： 由，∴a=2b． ，得 ，由余弦定理，得 ；（Ⅱ）解：由（Ⅰ），可得 ，代入 asinA=4bsinB，得 ．由（Ⅰ）知，A 为钝角，则 B 为锐角， ∴．，于是 故，．【点评】本题考查三角形的解法，考查正弦定理和余弦定理在解三角形中的应用 ，是中档题． 16．（13 分）（2017•天津）电视台播放甲、乙两套连续剧，每次播放连续剧时 ，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播 放时长、收视人次如下表所示： 连续剧播放时长（分钟） 广告播放时长（分钟） 收视人次（万） 70 60 5560 25 甲乙已知电视台每周安排的甲、乙连续剧的总播放时间不多于 600 分钟，广告的总播 放时间不少于 30 分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的 2 倍． 分别用 x，y 表示每周计划播出的甲、乙两套连续剧的次数． （I）用 x，y 列出满足题目条件的数学关系式，并画出相应的平面区域； （II）问电视台每周播出甲、乙两套连续剧各多少次，才能使总收视人次最多？ 【分析】（Ⅰ）直接由题意结合图表列关于 x，y 所满足得不等式组，化简后即 可画出二元一次不等式所表示的平面区域； （Ⅱ）写出总收视人次 z=60x+25y．化目标函数为直线方程的斜截式，数形结合 第 16 页（共 25 页） 第 17 页 共 25 页 得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案． 【解答】（Ⅰ）解：由已知，x，y 满足的数学关系式为 ，即 ．该二元一次不等式组所表示的平面区域如图： （Ⅱ）解：设总收视人次为 z 万，则目标函数为 z=60x+25y． 考虑 z=60x+25y，将它变形为 ，这是斜率为 ，随 z 变化的一族平 行直线． 为直线在 y 轴上的截距，当 取得最大值时，z 的值最大． 又∵x，y 满足约束条件， ∴由图可知，当直线 z=60x+25y 经过可行域上的点 M 时，截距 最大，即z 最 大． 解方程组 ，得点 M 的坐标为（6，3）． ∴电视台每周播出甲连续剧 6 次、乙连续剧 3 次时才能使总收视人次最多． 【点评】本题考查解得线性规划的应用，考查数学建模思想方法及数形结合的解 第 17 页（共 25 页） 第 18 页 共 25 页 题思想方法，是中档题． 17．（13 分）（2017•天津）如图，在四棱锥 P﹣ABCD 中，AD⊥平面 PDC，AD∥ BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2． （Ⅰ）求异面直线 AP 与 BC 所成角的余弦值； （Ⅱ）求证：PD⊥平面 PBC； （Ⅲ）求直线 AB 与平面 PBC 所成角的正弦值． 【分析】（Ⅰ）由已知 AD∥BC，从而∠DAP 或其补角即为异面直线 AP 与 BC 所 成的角，由此能求出异面直线 AP 与 BC 所成角的余弦值． （Ⅱ）由 AD⊥平面 PDC，得 AD⊥PD，由 BC∥AD，得 PD⊥BC，再由 PD⊥PB， 得到 PD⊥平面 PBC． （Ⅲ）过点 D 作 AB 的平行线交 BC 于点 F，连结 PF，则 DF 与平面 PBC 所成的角 等于 AB 与平面 PBC 所成的角，由 PD⊥平面 PBC，得到∠DFP 为直线 DF 和平面 PBC 所成的角，由此能求出直线 AB 与平面 PBC 所成角的正弦值． 【解答】解：（Ⅰ）如图，由已知 AD∥BC， 故∠DAP 或其补角即为异面直线 AP 与 BC 所成的角． 因为 AD⊥平面 PDC，所以 AD⊥PD． 在 Rt△PDA 中，由已知，得 ，故．所以，异面直线 AP 与 BC 所成角的余弦值为 ．证明：（Ⅱ）因为 AD⊥平面 PDC，直线 PD⊂平面 PDC， 所以 AD⊥PD． 又因为 BC∥AD，所以 PD⊥BC， 第 18 页（共 25 页） 第 19 页 共 25 页 又 PD⊥PB，所以 PD⊥平面 PBC． 解：（Ⅲ）过点 D 作 AB 的平行线交 BC 于点 F，连结 PF， 则 DF 与平面 PBC 所成的角等于 AB 与平面 PBC 所成的角． 因为 PD⊥平面 PBC，故 PF 为 DF 在平面 PBC 上的射影， 所以∠DFP 为直线 DF 和平面 PBC 所成的角． 由于 AD∥BC，DF∥AB，故 BF=AD=1， 由已知，得 CF=BC﹣BF=2．又 AD⊥DC，故 BC⊥DC， 在 Rt△DCF 中，可得 ．所以，直线 AB 与平面 PBC 所成角的正弦值为 ．【点评】本小题主要考查两条异面直线所成的角、直线与平面垂直、直线与平面 所成的角等基础知识．考查空间想象能力、运算求解能力和推理论证能力，是中 档题． 18．（13 分）（2017•天津）已知{an}为等差数列，前 n 项和为 Sn（n∈N*），{bn} 是首项为 2 的等比数列，且公比大于 0，b2+b3=12，b3=a4﹣2a1，S11=11b4． （Ⅰ）求{an}和{bn}的通项公式； （Ⅱ）求数列{a2nbn}的前 n 项和（n∈N*）． 【分析】（Ⅰ）设等差数列{an}的公差为 d，等比数列{bn}的公比为 q．通过 b2+b3=12，求出 q，得到 ．然后求出公差 d，推出 an=3n﹣2． （Ⅱ）设数列{a2nbn}的前 n 项和为 Tn，利用错位相减法，转化求解数列{a2nbn} 的前 n 项和即可． 【解答】（Ⅰ）解：设等差数列{an}的公差为 d，等比数列{bn}的公比为 q．由 第 19 页（共 25 页） 第 20 页 共 25 页 已知 b2+b3=12，得 q=2．所以， ，而 b1=2，所以 q2+q﹣6=0．又因为 q＞0，解得 ．由 b3=a4﹣2a1，可得 3d﹣a1=8． 由 S11=11b4，可得 a1+5d=16，联立①②，解得 a1=1，d=3， 由此可得 an=3n﹣2． 所以，{an}的通项公式为 an=3n﹣2，{bn}的通项公式为 ．（ Ⅱ ） 解 ： 设 数 列 {a2nbn} 的 前n 项 和 为Tn ， 由a2n=6n﹣2 ， 有 ，，上 述 两 式 相 减 ， 得 =．得．所以，数列{a2nbn}的前 n 项和为（3n﹣4）2n+2+16． 【点评】本题考查等差数列以及等比数列通项公式的求法，数列求和，考查转化 思想以及计算能力． 19．（14 分）（2017•天津）设 a，b∈R，|a|≤1．已知函数 f（x）=x3﹣6×2﹣3a （a﹣4）x+b，g（x）=exf（x）． （Ⅰ）求 f（x）的单调区间； （Ⅱ）已知函数 y=g（x）和 y=ex 的图象在公共点（x0，y0）处有相同的切线， （i）求证：f（x）在 x=x0 处的导数等于 0； （ii）若关于 x 的不等式 g（x）≤ex 在区间[x0﹣1，x0+1]上恒成立，求 b 的取值 范围． 【分析】（Ⅰ）求出函数 f（x）的导函数，得到导函数的零点，由导函数的零点 第 20 页（共 25 页） 第 21 页 共 25 页 对定义域分段，列表后可得 f（x）的单调区间； （Ⅱ）（i ）求出 g （x ）的导函数，由题意知 ．得到 f（x）在 x=x0 处的导数等于 0； ，求解可得 （ii）由（I）知 x0=a．且 f（x）在（a﹣1，a）内单调递增，在（a，a+1）内单 调递减，故当 x0=a 时，f（x）≤f（a）=1 在[a﹣1，a+1]上恒成立，从而 g（x）≤ ex 在 [x0﹣1 ， x0+1] 上 恒 成 立 ． 由f （ a ） =a3﹣6a2﹣3a （ a﹣4 ） a+b=1 ， 得 b=2a3﹣6a2+1，﹣1≤a≤1．构造函数 t（x）=2×3﹣6×2+1，x∈[﹣1，1]，利用导 数求其值域可得 b 的范围． 【解答】（Ⅰ）解：由 f（x）=x3﹣6×2﹣3a（a﹣4）x+b，可得 f’（x）=3×2﹣12x﹣3a （a﹣4）=3（x﹣a）（x﹣（4﹣a））， 令 f’（x）=0，解得 x=a，或 x=4﹣a．由|a|≤1，得 a＜4﹣a． 当 x 变化时，f’（x），f（x）的变化情况如下表： x（﹣∞，a） （a，4﹣a） （4﹣a，+∞） ﹣f’（x） f（x） ++↗↘↗∴f（x）的单调递增区间为（﹣∞，a），（4﹣a，+∞），单调递减区间为（a， 4﹣a）； （Ⅱ）（i）证明：∵g’（x）=ex（f（x）+f’（x）），由题意知 ，∴，解得 ．∴f（x）在 x=x0 处的导数等于 0； 第 21 页（共 25 页） 第 22 页 共 25 页 （ii）解：∵g（x）≤ex，x∈[x0﹣1，x0+1]，由 ex＞0，可得 f（x）≤1． 又∵f（x0）=1，f’（x0）=0， 故 x0 为 f（x）的极大值点，由（I）知 x0=a． 另一方面，由于|a|≤1，故 a+1＜4﹣a， 由（Ⅰ）知 f（x）在（a﹣1，a）内单调递增，在（a，a+1）内单调递减， 故当 x0=a 时，f（x）≤f（a）=1 在[a﹣1，a+1]上恒成立，从而 g（x）≤ex 在[x0﹣1 ，x0+1]上恒成立． 由 f（a）=a3﹣6a2﹣3a（a﹣4）a+b=1，得 b=2a3﹣6a2+1，﹣1≤a≤1． 令 t（x）=2×3﹣6×2+1，x∈[﹣1，1]， ∴t’（x）=6×2﹣12x， 令 t’（x）=0，解得 x=2（舍去），或 x=0． ∵t（﹣1）=﹣7，t（1）=﹣3，t（0）=1，故 t（x）的值域为[﹣7，1]． ∴b 的取值范围是[﹣7，1]． 【点评】本题考查利用导数研究函数的单调性，考查了利用研究过曲线上某点处 的切线方程，训练了恒成立问题的求解方法，体现了数学转化思想方法，是压轴 题． 20．（14 分）（2017•天津）已知椭圆 +=1（a＞b＞0）的左焦点为 F（﹣c ，0），右顶点为 A，点 E 的坐标为（0，c），△EFA 的面积为 （I）求椭圆的离心率； ．（II）设点 Q 在线段 AE 上，|FQ|= c，延长线段 FQ 与椭圆交于点 P，点 M，N 在 x 轴上，PM∥QN，且直线 PM 与直线 QN 间的距离为 c，四边形 PQNM 的面 积为 3c． （i）求直线 FP 的斜率； （ii）求椭圆的方程． 第 22 页（共 25 页） 第 23 页 共 25 页 【分析】（Ⅰ）设椭圆的离心率为 e．通过 率． （Ⅱ）（ⅰ）依题意，设直线 FP 的方程为 x=my﹣c（m＞0），则直线 FP 的斜 率为 ．通过a=2c，可得直线 AE 的方程为 ，求解点Q 的坐标为 ．利用|FQ|= ，求出 m，然后求解直线 FP 的斜率． （ii）求出椭圆方程的表达式你，求出直线 FP 的方程为 3x﹣4y+3c=0，与椭圆方 ．转化求解椭圆的离心 程联立通过 ，结合直线PM 和 QN 都垂直于直线 FP． 结合四边形 PQNM 的面积为 3c，求解 c，然后求椭圆的方程． 【解答】解：（Ⅰ）设椭圆的离心率为 e．由已知，可得 ．又由 ．b2=a2﹣c2，可得 2c2+ac﹣a2=0，即 2e2+e﹣1=0．又因为 0＜e＜1，解得 所以，椭圆的离心率为 ； （Ⅱ）（ⅰ）依题意，设直线 FP 的方程为 x=my﹣c（m＞0），则直线 FP 的斜 率为 ． 由（Ⅰ）知 a=2c，可得直线 AE 的方程为 ，即 x+2y﹣2c=0，与直线 FP ，即点 Q 的坐标为 ，整理得 3m2﹣4m=0，所 的方程联立，可解得 ．由已知|FQ|= ，有 以，即直线 FP 的斜率为 ． （ii）解：由 a=2c，可得 ，故椭圆方程可以表示为 ．由（i）得直线 FP 的方程为 3x﹣4y+3c=0，与椭圆方程联立 消去 y， 整理得 7×2+6cx﹣13c2=0，解得 （舍去），或 x=c．因此可得点 第 23 页（共 25 页） 第 24 页 共 25 页 ，进而可得 ，所以 ．由已 知，线段 PQ 的长即为 PM 与 QN 这两条平行直线间的距离，故直线 PM 和 QN 都 垂直于直线 FP． 因为 QN⊥FP，所以 ，同理¡÷FPM 的面积等于 ，所以¡÷FQN 的面积为 ，由四边形 PQNM 的面积为 3c ，得 ，整理得 c2=2c，又由 c＞0，得 c=2． 所以，椭圆的方程为 ．【点评】本题考查椭圆的方程的求法，直线与椭圆的位置关系的综合应用，考查 转化思想以及计算能力． 第 24 页（共 25 页） 第 25 页 共 25 页 参与本试卷答题和审题的老师有：zlzhan；maths；qiss；742048；sxs123； danbo7801；双曲线；caoqz（排名不分先后） 菁优网 2017 年 6 月 26 日 第 25 页（共 25 页）
声明：如果本站提供的资源有问题或者不能下载，请点击页面底部的"联系我们"；
本站提供的资源大部分来自网络收集整理，如果侵犯了您的版权，请联系我们删除。
