2022年高考数学真题（理科）（全国乙卷）（解析版）下载

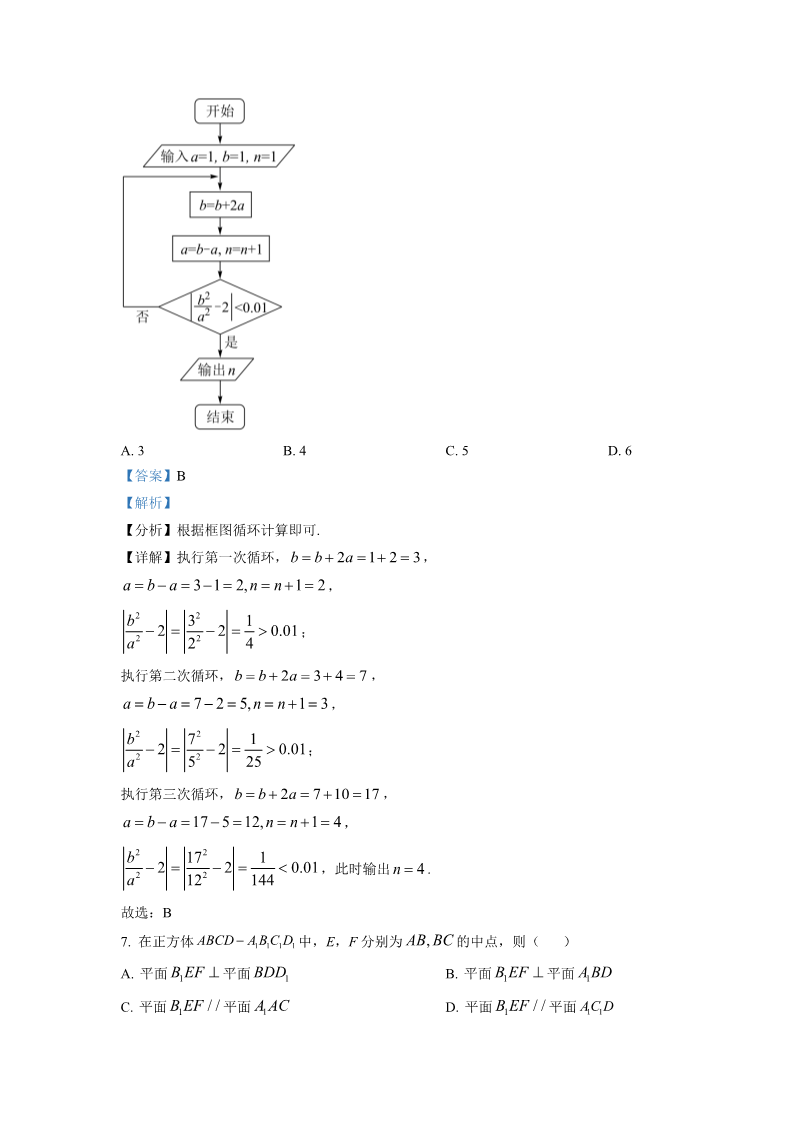
绝密 启用前 ★2022 年普通高等学校招生全国统一考试 数学（理科） 注意事项： 1．答卷前，考生务必将自己的姓名和座位号填写在答题卡上． 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标 号涂黑.如需改动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时， 将答案写在答题卡上.写在本试卷上无效． 3．考试结束后，将本试卷和答题卡一并交回． 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选 项中，只有一项是符合题目要求的． U {1,2,3,4,5} ð M  {1,3} 1. 设全集 ，集合 M 满足 ，则（ ）UA. B. C. D. 3 M 4 M 5M 2M 【答案】A 【解析】 M【分析】先写出集合 ,然后逐项验证即可 M {2,4,5} 【详解】由题知 故选: ,对比选项知， 正确, 错误 BCD AA2. 已知 ，且 ，其中 a，b 为实数，则（ ）z 1 2i z  az  b  0 a 1,b  2 a  1,b  2 a 1,b  2 A. B. C. D. a  1,b  2 【答案】A 【解析】 【分析】先算出 【详解】 ,再代入计算,实部与虚部都为零解方程组即可 zz  1  2i z  az  b 1 2i  a(1 2i)  b  (1 a  b)  (2a  2)i 1 a  b  0 a 1 由,得 ,即 z  az  b  0 2a  2  0 b  2 故选: A    3. 已知向量 满足 ，则 （）a,b | a | 1,|b | 3,| a  2b | 3 ab  A. 2 B. C. 1 D. 2 1 【答案】C 【解析】 【分析】根据给定模长，利用向量的数量积运算求解即可.  2 【详解】解：∵| a  2b |2 | a |2 4a b  4 b ，又∵ ∴9 | a |1,| b | 3,| a  2b | 3, ，1 4a b  43 13 4a b ∴a b 1 故选：C. 的4. 嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行 b人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列  ：n11b3  1 1b2  1 1b  1 1  1，，，…，依此类推，其中 111  1 2  2 3  N(k  1,2,) ．则（ ）kb  b5 b3  b8 b6  b2 b4  b7 D. AB. C. 1【答案】D 【解析】  N* k 1,2,… bb【分析】根据 ，再利用数列  与k 的关系判断 中各项的大 knn小，即可求解. 【详解】解：因为  N* k 1,2, ，k111    1b  b 所以 同理 ，1 ，得到 ，11121  2 2 111   1  1b  b b  b ，2 ，可得 23132  3 1111,1   1  1112 2  2  2  又因为 ，113 3  3  4 4 b  b b b ，故；2434b  b  b  b … b  b 8 ，故 A 错误； 以此类推，可得 ，13577b  b  b 8 ，故 B 错误； 171112 2  b  b ，得 6 ，故 C 错误； 213 … 6 111111   1  2  2 … b  b ，得 7 ，故 D 正确. 413  6  4 7 故选：D. 2B(3,0) AF  BF 5. 设 F 为抛物线 AB  的焦点，点 A 在 C 上，点 ，若 ，则 C : y  4x （）A. 2 B. C. 3 D. 2 2 3 2 【答案】B 【解析】 【分析】根据抛物线上的点到焦点和准线的距离相等，从而求得点 A的横坐标，进而求得 点A坐标，即可得到答案. F 1,0 AF  BF  2 【详解】由题意得， ，则 ，即点 A到准线 的距离为 2，所以点 A 1,2 ，A的横坐标为 1 2 1， x  1 x不妨设点 所以 A在 轴上方，代入得， 22.AB  31  0  2  2 2 故选：B n  6. 执行下边的程序框图，输出的 （）A. 3 B. 4 C. 5 D. 6 【答案】B 【解析】 【分析】根据框图循环计算即可. 【详解】执行第一次循环，b  b  2a 1 2  3 ，a  b  a  31 2,n  n 1 2 ，b2 a2 32 22 1 2   2  0.01 ；4执行第二次循环，b  b  2a  3 4  7 ，a  b  a  7  2  5,n  n 1 3 ，b2 a2 72 52 1 2   2   0.01 ；25 执行第三次循环，b  b  2a  7 10 17 ，a  b  a 17 5 12,n  n 1 4 ，b2 a2 172 122 1 2   2   0.01 ，此时输出 .n  4 144 故选：B ABCD  A B C D 1 中，E，F 分别为 AB, BC 7. 在正方体 的中点，则（ ）平面 平面 111B EF  BDD B EF  A BD A. 平面 C. 平面 平面 平面 B. 平面 1111B EF / / A AC B EF / / AC D D. 平面 11111【答案】A 【解析】 BDD D1 ，即可判断 A；如图，以点 为原点，建立空间直角坐标 【分析】证明 平面 EF  B EFA BDAC D 系，设 ，分别求出平面 ，，的法向量，根据法向量的位置关 AB  2 1111系，即可判断 BCD. ABCD  A B C D 【详解】解：在正方体 1 中， 111DD  AC  BD 且平面 ，ABCD 1EF  DD 又EF  平面 ，所以 ，ABCD 1E, F AB, BC 的中点， 因为 所以 分别为 EF  AC ，所以 ，EF  BD BD  DD  D 又，1BDD 所以 平面 ，EF  1B EF 又EF  平面 ，1B EF  BDD 1 ，故 A 正确； 所以平面 平面 1如图，以点 D为原点，建立空间直角坐标系，设 ，AB  2 B 2,2,2 ,E 2,1,0 ,F 1,2,0 ,B 2,2,0 ,A 2,0,2 ,A 2,0,0 ,C 0,2,0 则1  1  ，C 0,2,2 ，1    1EF  1,1,0 ,EB  0,1,2 DB  2,2,0 ,DA  2,0,2 则，，1   AA  0,0,2 ,AC  2,2,0 ,AC  2,2,0 , 111 m  x , y , z B EF 设平面 的法向量为 ，1  111  m EF  x  y  0 11 m  2,2,1 则有 ，可取 ，m EB  y  2z  0 111 A BD n  1,1,1 同理可得平面 的法向量为 ，11 A AC n  1,1,0 平面 平面 的法向量为 ，12 AC D n  1,1,1 的法向量为 ，113  mn1  2  2 11 0 则，B EF A BD 不垂直，故 B 错误； 1所以平面 与平面 1uur  因为 与2 不平行， nmB EF A AC 所以平面 与平面 不平行，故 C 错误； 不平行，故 D 错误， 11  因为 与n3 不平行， mB EF AC D 与平面 1所以平面 11故选：A. a  a  42 aa  8. 已知等比数列 的前 3 项和为 168， ，则 （）  25n6A. 14 B. 12 C. 6 D. 3 【答案】D 【解析】 aq,q  0 q 1 【分析】设等比数列 的公比为 ，易得 ，根据题意求出首项与公比，再根 n据等比数列的通项即可得解. aq,q  0 【详解】解：设等比数列 的公比为 ，nq 1 a  a  0 若，则 ，与题意矛盾， 25q 1 所以 ，a 1 q3 1  a  96 1a1  a2  a3  168 则，解得 ，11 q q  a2  a5  a1q  a1q4  42 2a  a q5  3 所以 .61故选：D. 9. 已知球 O 的半径为 1，四棱锥的顶点为 O，底面的四个顶点均在球 O 的球面上，则当该 四棱锥的体积最大时，其高为（ ）131232A. B. C. D. 32【答案】C 【解析】 【分析】先证明当四棱锥的顶点 O 到底面 ABCD 所在小圆距离一定时，底面 ABCD 面积最 大值为 2，进而得到四棱锥体积表达式，再利用均值定理去求四棱锥体积的最大值，从而 2r 得到当该四棱锥的体积最大时其高的值. 【详解】设该四棱锥底面为四边形 ABCD，四边形 ABCD 所在小圆半径为 r， 设四边形 ABCD 对角线夹角为 ，111S AC  BDsin  AC  BD  2r 2r  2r2 则ABCD 222（当且仅当四边形 ABCD 为正方形时等号成立） 2即当四棱锥的顶点 O 到底面 ABCD 所在小圆距离一定时，底面 ABCD 面积最大值为 2r 22又r  h  1 2 3 22122r  r  2h 4 3 27 VOABCD  2r2 h  r2 r2 2h2  则3333322h  当且仅当 即时等号成立， r  2h 3故选：C 10. 某棋手与甲、乙、丙三位棋手各比赛一盘，各盘比赛结果相互独立．已知该棋手与 p , p , p p  p  p  0 的甲、乙、丙比赛获胜 概率分别为 3 ，且 ．记该棋手连胜两盘的 12321概率为 p，则（ ）A. p 与该棋手和甲、乙、丙的比赛次序无关 C. 该棋手在第二盘与乙比赛，p 最大 【答案】D B. 该棋手在第二盘与甲比赛，p 最大 D. 该棋手在第二盘与丙比赛，p 最大 【解析】 【分析】该棋手连胜两盘，则第二盘为必胜盘.分别求得该棋手在第二盘与甲比赛且连胜两 pp盘的概率 甲 ；该棋手在第二盘与乙比赛且连胜两盘的概率 乙 ；该棋手在第二盘与丙比赛 p且连胜两盘的概率 丙 .并对三者进行比较即可解决 【详解】该棋手连胜两盘，则第二盘为必胜盘， 记该棋手在第二盘与甲比赛，且连胜两盘的概率为 p甲p  2(1 p ) p p 2p p(1 p )  2p ( p  p )  4p p p 则甲213213123123p记该棋手在第二盘与乙比赛，且连胜两盘的概率为 乙p  2(1 p ) p p  2p p (1 p )  2p ( p  p )  4p p p 则乙123123213123p记该棋手在第二盘与丙比赛，且连胜两盘的概率为 丙p  2(1 p ) p p  2p p (1 p )  2p ( p  p )  4p p p 则则132132312123丙p  p  2p ( p  p )  4p p p  2p ( p  p )  4p p p 2 p  p p 0 2  3  甲乙1231232131213p  p  2p ( p  p )  4p p p  2p ( p  p )  4p p p 2 p  p p 0 3  3  乙2131233121221丙p  p p  p 即，，甲乙乙丙p则该棋手在第二盘与丙比赛， 最大.选项 D 判断正确；选项 BC 判断错误； p与该棋手与甲、乙、丙的比赛次序有关.选项 A 判断错误. 故选：D F , F F11. 双曲线 C 的两个焦点为 2 ，以 C 的实轴为直径的圆记为 D，过 1 作 D 的切线与 C 13cosF NF 的两支交于 M，N 两点，且 ，则 C 的离心率为（ ）1253213 C. 17 25A. B. D. 22【答案】C 【解析】 x【分析】依题意不妨设双曲线焦点在 轴，设过 1 作圆 FD的切线切点为 G，可判断 在NF NF  F F N   ，sin  cos  ，双曲线的右支，设 ，即可求出sin ，，在 ，1221F F N sin F F N  sin    sin F F N NF ，再由正弦定理求出 1中由 求出 211212NF2 ，最后根据双曲线的定义得到 ，即可得解； 2b  3a x【详解】解：依题意不妨设双曲线焦点在 轴，设过 1 作圆 FD的切线切点为 G，3OG  NF cosF NF 0 所以 所以 1 ，因为 ，所以 在双曲线的右支， N125OG  a OF c GF  b F NF  F F N   ，，，，设 ，111221353545abccosF NF cos  sin = sin   cos   由在，即 ，则 ，，，12cF F N sin F F N  sin      sin    中， 211 2 4 b 3 a 3a  4b  sin cos   cos sin       5 c 5 c ，5c NF2 NF 12c 5c 由正弦定理得 ，sin sin  sin F F2 N 215c NF  sin F F2 N  5c 3a  4b 3a  4b 5c 5c a5a NF  sin    所以 ，112225c 222c23a  4b 5a 4b  2a NF  NF   2a 又，12222ba32所以 ，即 ，2b  3a cb2 a2 13 2所以双曲线的离心率 e  1 a故选：C f (x), g(x) 12. 已知函数 的定义域均为 R，且 f (x)  g(2  x)  5, g(x)  f (x  4)  7 y  g(x) x  2 ．若 的图像关于直线 对称， 22 g(2)  4 f (k)  ，则 （）k1 A. B. C. D. 23 21 22 24 【答案】D 【解析】 f (x)  f (x  2)  2 【分析】根据对称性和已知条件得到 ，从而得到 f 3  f 5  f 21  10 f 4  f 6  f 22  10      ，，然后根据条件得 f (2) g 3  6 的值，再由题意得到   f 1 到从而得到  的值即可求解. y  g(x) x  2 【详解】因为 的图像关于直线 对称， g 2  x  g x 2 所以 ，g(x)  f (x  4)  7 f (x)  g(2  x)  5 g(x  2)  f (x  2)  7 g(x  2)  7  f (x  2) 因为 因为 ，所以 ，即 ，f (x)  g(x  2)  5 ，所以 ，f (x)  7  f (x  2)  5 f (x)  f (x  2)  2 代入得 ，即 ，f 3  f 5  f 21  2 5  10 所以      ，f 4  f 6  f 22  2 5  10       .f (x)  g(2  x)  5 f (0)  g(2)  5 f 0 1 ，即   因为 ，所以 ，所以 f (2)  2  f 0  3   .g(x)  f (x  4)  7 g(x  4)  f (x)  7 f (x)  g(2  x)  5 因为 ，所以 ，又因为 ，g 2  x  g x 4 12 联立得， ，g(x) 的定义域为 R， y  g(x) g 3  6 3,6 中心对称，因为函数 所以 的图像关于点 所以   f (x)  g(x  2)  5 f 1  5 g 3  1 ，所以     因为 .所以 22 f (k)  f 1  f 2   f 3  f 5  f 21    f 4  f 6  f 22   1310 10  24          k1 .故选：D 【点睛】含有对称轴或对称中心的问题往往条件比较隐蔽，考生需要根据已知条件进行恰 当的转化，然后得到所需的一些数值或关系式从而解题. 二、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13. 从甲、乙等 5 名同学中随机选 3 名参加社区服务工作，则甲、乙都入选的概率为 ____________． 3【答案】 【解析】 ##0.3 10 【分析】根据古典概型计算即可 C3 10 【详解】从 5 名同学中随机选 3 名的方法数为 53C1  3 P  甲、乙都入选的方法数为 ，所以甲、乙都入选的概率 310 3故答案为： 10 (0,0),(4,0),(1,1),(4,2) 14. 过四点 中的三点的一个圆的方程为____________． 222222437365 9【答案】 x  2  y 3 13 或x  2  y 1  5 或或x   y  285169 25 2；x   y 1  【解析】 x2  y2  Dx  Ey  F  0 【分析】设圆的方程为 即可； ，根据所选点的坐标，得到方程组，解得 x2  y2  Dx  Ey  F  0 【详解】解：依题意设圆的方程为 ，F  0 F  0 1,1 0,0 4,0 16  4D  F  0 D  4 E  6 若过 ，，，则 ，解得 ，11 D  E  F  0 22所以圆的方程为 x2  y2  4x  6y  0 ，即 x  2  y 3 13 ；F  0 F  0 0,0 4,0 4,2 16  4D  F  0 D  4 E  2 若过 ，，，则 ，解得 ，16  4  4D  2E  F  0 22所以圆的方程为 x2  y2  4x  2y  0 ，即 x  2  y 1  5 ；F  0 F  0 81,1 0,0 4,2 11 D  E  F  0 D   E   若过 ，，，则 ，解得 ，316  4  4D  2E  F  0 14 322814 437365 x2  y2  x  y  0 所以圆的方程为 ，即 ；x   y  33916 516 5F   D   11 D  E  F  0 1,1 4,0 4,2 16  4D  F  0 若过 ，，，则 ，解得 ，16  4  4D  2E  F  0 E  2 216 16 85169 2x2  y2  x  2y  0 所以圆的方程为 ，即 ；x   y 1  5525 222222437365 9故答案为： x  2  y 3 13 或x  2  y 1  5 或x   y  285169 25 2或；x   y 1  3f x cos x  (  0,0    π) 15. 记函数 的最小正周期为 T，若 ，  f (T)  29f (x) 的零点，则 的最小值为____________． x  为【答案】 【解析】 3π3求出 ，再根据 x  【分析】首先表示出 ，根据 T为函数的零点，即可求出 f T    92的取值，从而得解； f x cos x  0    π 【详解】解： 因为  ，（ ，）  0 2π 2π 3T  所以最小正周期 ，因为 f T  cos     cos 2π   cos  ，  2ππ0    π f x cos x  ，即     又又，所以 ，66ππππf x   3 9k,k Z x     3  kπ,k Z 为 的零点，所以 ，解得 ，9962因为 ，所以当 时；  0 k  0 min 故答案为： 3x2x  x x  x 1 和 16. 已知 分别是函数 （且a  0 a 1 ）的极小值点和极 f (x)  2a  e x 2x  x 大值点．若 2 ，则 a 的取值范围是____________． 11,1 【答案】 e【解析】 x , x 2 分别是函数   f x 2ax  e x2 【分析】由 的极小值点和极大值点，可得 1f x 0 x , x  x , f x 0 x x , x 时，   2  时，   a 1 和1  ，，再分 212 ，即函数 y  ln aax x , x 两种情况讨论，方程 与x0  a 1 的两个根为 2ln aa  2e x  0 1g x  ln aax y  e x 函数 的图象有两个不同的交点，构造函数   ，根据导数的结合意义结 合图象即可得出答案. xf x 2ln aa  2e x 【详解】解：   ，x , x f x 2ax  e x2 因为 2 分别是函数   的极小值点和极大值点， 1f x 所以函数   , x 1  x , x , x 在和上递减，在 2  上递增， 21x , x  x , f x 0 时，   x x , x f x 0 所以当 1  ，当 2  时，   ，21a 1 若当时， 时， 2ln aax  0,2e x  0 ，x  0 f x 0 则此时   ，与前面矛盾， a 1 故不符合题意， 0  a 1 若时， xx , x ，2则方程 即方程 的两个根为 2ln aa  2e x  0 1xx , x 的两个根为 ，ln aa  e x 12即函数 y  ln aax 与函数 的图象有两个不同的交点， y  e x 2xg x  ln aax g x ln aa ,0  a 1 令  ，则   ，x ,ln aax 0y  g x 设过原点且与函数  的图象相切的直线的切点为 ，0x0 2g x  ln aa 则切线的斜率为   ，0y  ln aax0  ln2 aax0 x  x 故切线方程为 0  ，ln aax0  x ln2 aax0 则有 ，01x  解得 ，0ln a 122则切线的斜率为 ，ln aalna  eln a 因为函数 y  ln aax 与函数 的图象有两个不同的交点， y  e x 12 a  e 所以 ，解得 ，eln a  e e1e0  a 1  a 1 又，所以 ，1ea综上所述， 的范围为 ,1 .【点睛】本题考查了函数的极值点问题，考查了导数的几何意义，考查了转化思想及分类 讨论思想，有一定的难度. 三、解答题：共 0 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考生都必须作答．第 22、23 题为选考题，考生根据要 求作答． （一）必考题：共 60 分． A, B,C a,b,c ，已知 17. 记 的内角 的对边分别为 ABC sinC sin(A B)  sin Bsin(C  A) ．222（1）证明： ；2a  b  c 25 31 a  5,cos A  （2）若 ，求 的周长． ABC 【答案】（1）见解析 （2）14 【解析】 【分析】（1）利用两角差的正弦公式化简，再根据正弦定理和余弦定理化角为边，从而即 可得证； （2）根据（1）的结论结合余弦定理求出bc ，从而可求得b  c ，即可得解. 【小问 1 详解】 sinC sin A B  sin Bsin C  A 证明：因为 ，所以sinC sin Acos B sinC sin Bcos A  sin BsinC cos Asin Bsin AcosC ，a2  c2 b2 2ac b2  c2  a2 2bc a2  b2  c2 2ab 所以 ，ac  2bc  ab a2  c2 b2 a2  b2  c2  b2  c2  a2   即，22222所以 ；2a  b  c 【小问 2 详解】 25 31 a  5,cos A  解：因为 ，22由（1）得 由余弦定理可得 50 ，b  c  50 222，a  b  c  2bccos A 50  bc  25 则，31 31 bc  所以 ，2222故，b  c  b  c  2bc  50  31 81 所以 所以 ，b  c  9 的周长为 a  b  c 14 .ABC AD  CD, AD  CD,ADB  BDC 18. 如图，四面体 中， ，E 为 的中 ABCD AC 点． （1）证明：平面 平面 ；ACD BED  AB  BD  2,ACB  60 （2）设 ，点 F 在 上，当△AFC 的面积最小时，求 CF BD 与平面 ABD 所成的角的正弦值． 【答案】（1）证明过程见解析 4 3 （2） 与平面 ABD 所成的角的正弦值为 CF 7【解析】 【分析】（1）根据已知关系证明 ，得到 ，结合等腰三角形三线 △ABD≌△CBD AB  CB 合一得到垂直关系，结合面面垂直的判定定理即可证明； （2）根据勾股定理逆用得到 则进行计算即可. ，从而建立空间直角坐标系，结合线面角的运算法 BE  DE 【小问 1 详解】 AC  DE ；因为 在，E 为 的中点，所以 AD  CD AC AD  CD,ADB  CDB, DB  DB 和中，因为 ，△ABD CBD 所以 ，所以 ，又因为 E 为 的中点，所以 AC  BE ；△ABD≌△CBD AB  CB AC DE, BE  AC  又因为 平面 ，，所以 平面 ，DE  BE  E BED BED AC  因为 【小问 2 详解】 连接 ，由（1）知， 平面 ，所以平面 平面 .ACD ACD BED  AC  平面 ，因为 EF  平面 ，EF BED BED 1S= AC  EF 所以 AC  EF ，所以 ，△AFC 2当时， 最小，即△AFC 的面积最小. EF EF  BD 因为 ，所以 ，△ABD≌△CBD CB  AB  2 又因为 ，所以 是等边三角形， ACB  60 ABC 因为 E 为 的中点，所以 ，，AC AE  EC 1 BE  3 1AD  CD DE  AC 1 因为 在，所以 ,222中， 2 ，所以 .DEB BE  DE DE  BE  BD E  xyz ，以为坐标原点建立如图所示的空间直角坐标系 E  A 1,0,0 ,B 0, 3,0, D 0,0,1 AD  1,0,1 ,AB  1, 3,0 则，所以 ，n  x, y, z 设平面 ABD 的一个法向量为 ，  n  AD  x  z  0 n  3, 3,3 则，取 ，则 ，，y  3 n  AB  x  3y  0  3 3 ,3 3 ,C 1,0,0 ,F 0, CF  1, 又因为 ，所以 4 4 4 4     cos n,CF  nCF 674 3   所以 ，7n CF 21 42 0   设与平面 ABD 所成的角的正弦值为 ，CF   4 3 所以 所以 ，sin  cos n,CF  74 3 与平面 ABD 所成的角的正弦值为 .CF 719. 某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总 材积量，随机选取了 10 棵这种树木，测量每棵树的根部横截面积（单位： 2 ）和材积量 m（单位： 3 ），得到如下数据： m总样本号ｉ 12345678910 和根部横截面积 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06 0.6 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40 3.9 xi y材积量 i10 10 10 x2  0.038, y2 1.6158, x y 0.2474 并计算得 ．iiiii=1 i=1 i=1 （1）估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量； （2）求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到 0.01）； （3）现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积 总和为 2 ．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林 186m 区这种树木的总材积量的估计值． n(x  x)(y  y) iii=1 r  , 1.8961.377 ．附：相关系数 nn(x  x)2 (y  y)2 iii=1 i=1 23【答案】（1） ；0.06m 0.39m （2） 0.97 3（3） 1209m 【解析】 【分析】（1）计算出样本的一棵根部横截面积的平均值及一棵材积量平均值，即可估计该 林区这种树木平均一棵的根部横截面积与平均一棵的材积量； （2）代入题给相关系数公式去计算即可求得样本的相关系数值； （3）依据树木的材积量与其根部横截面积近似成正比，列方程即可求得该林区这种树木的 总材积量的估计值． 【小问 1 详解】 0.6 x   0.06 样本中 10 棵这种树木的根部横截面积的平均值 10 3.9 y   0.39 样本中 10 棵这种树木的材积量的平均值 10 2据此可估计该林区这种树木平均一棵的根部横截面积为 ，0.06m 3平均一棵的材积量为 0.39m 【小问 2 详解】 10 10 x  x y y xi yi 10xy  iii=1 i=1 r  10 10 10 10 22 x  x y  y xi2 10×2 yi2 10y2 ii i=1 i=1 i=1 i=1 0.2474 100.060.39 (0.038100.062 )(1.6158100.392 ) 0.0134 0.0134  0.97 0.01377 0.0001896 r  0.97 则【小问 3 详解】 3设该林区这种树木的总材积量的估计值为 ，Ym 又已知树木的材积量与其根部横截面积近似成正比， 0.06 186 3=可得 ，解之得 ．Y=1209m 0.39 Y3则该林区这种树木的总材积量估计为 1209m 3A 0,2 ,B ,1 20. 已知椭圆 E 的中心为坐标原点，对称轴为 x 轴、y 轴，且过 两2点． （1）求 E 的方程； P 1,2 的直线交 E 于 M，N 两点，过 M 且平行于 x 轴的直线与线段 AB 交 （2）设过点   于点 T，点 H 满足 ．证明：直线 HN 过定点． MT  TH y2 x2 【答案】（1） 1 43(0,2) （2） 【解析】 【分析】（1）将给定点代入设出的方程求解即可； （2）设出直线方程，与椭圆 C 的方程联立，分情况讨论斜率是否存在，即可得解. 【小问 1 详解】 3解：设椭圆 E 的方程为 mx2  ny2 1，过 ，A 0,2 ,B ,1 24n 1 1413m  n  则，解得 ，，9 m  n 1 4 y2 x2 所以椭圆 E 的方程为： 【小问 2 详解】 .1 43323A(0,2), B( ,1) AB : y  2  x，，所以 2×2 y2 P(1,2) ①若过点 的直线斜率不存在，直线 .代入 ，x 1 1 3422 6 2 6 y  x  2 可得 ，，代入 AB 方程 )，可得 M (1, )N(1, 333  2 6 32 6 ，由 得到 .求得 HN 方程： )T( 6 3, )H(2 6 5, MT  TH 32 6 (0,2) ，过点 .y  (2  )x  2 3P(1,2) kx  y  (k  2)  0, M (x , y ), N(x , y ) .2②若过点 的直线斜率存在，设 112kx  y  (k  2)  0 联立 得(3k2  4)x2  6k(2  k)x  3k(k  4)  0 ，x2 y2 ,1 348(2  k) 3k2  4 6k(2  k) 3k2  4 y1  y2  x1  x2  可得 ，，4(4  4k  2k2 ) 3k2  4 3k(4  k) x1x2  y2 y2  3k2  4 24k x y x y  (*) 且122 1 3k2  4 y  y1 3y1 ,T( 可得  3, y1), H(3y1  6  x1, y1). y1  y2 联立 2y  x  2 23HN : y  y  (x  x ) 可求得此时 ，223y1  6  x1  x2 (0,2) 2(x  x )  6(y  y )  x y x y 3y y12  0 将将，代入整理得 ，121212211 2 代入，得 24k 12k2  96  48k  24k  48 48k  24k2 36k2  48  0, (*) 显然成立， (0,2). 综上，可得直线 HN 过定点 【点睛】求定点、定值问题常见的方法有两种： ①从特殊入手，求出定值，再证明这个值与变量无关； ②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值. f x ln 1 x  axex 21. 已知函数   y  f x 0, f 0 （1）当 a 1时，求曲线  在点   处的切线方程； f x 1,0 , 0,   （2）若  在区间 各恰有一个零点，求 a 的取值范围． y  2x 【答案】（1） (,1) （2） 【解析】 【分析】（1）先算出切点,再求导算出斜率即可 ax(1,0),(0,) （2）求导,对 分类讨论,对 分 两部分研究 【小问 1 详解】 f (x) (1,) 的定义域为 x(0,0) f (x)  ln(1 x)  , f (0)  0 当a 1时, ,所以切点为 ex , f  (0)  2 (0, f (0)) 11 x f  (x)  ,所以切线斜率为 2 1 x ex y  f (x) y  2x 所以曲线 在点 处的切线方程为 【小问 2 详解】 ax ex f (x)  ln(1 x)  ex  a 1 x2 1a(1 x) f  (x)  1 x ex (1 x)ex g(x)  ex  a 1 x2 设x(1,0), g(x)  ex  a 1 x2  0  若 ,当 ,即 f (x)  0 a  0 1f (x) (1,0) f (x)  f (0)  0 所以 在上单调递增, f (x) (1,0) 故在上没有零点,不合题意 x2 x(0,) 1„ a„ 0 若,当 ,则 g (x)  e  2ax  0 f (x)  0 ,即 g(x) f (x) (0,) (0,) g(x)  g(0) 1 a… 0 所以 所以 故在在上单调递增所以 f (x)  f (0)  0 上单调递增, f (x) (0,) 在上没有零点,不合题意 3 a  1 若xg(x) x(0,) (0,) (1)当 ,则 ,所以 在上单调递增 g (x)  e  2ax  0 g(0) 1 a  0, g(1)  e  0 m(0,1) g(m)  0 f (m)  0 ,即 所以存在 ,使得 当x(0,m), f  (x)  0, f (x) 单调递减 当 x(m,), f  (x)  0, f (x) 单调递增 所以 x(0,m), f (x)  f (0)  0 当x  , f (x)   当f (x) (m,) 所以 在上有唯一零点 f (x) (0,m) (0,) 又没有零点,即 在上有唯一零点 x(1,0), g(x)  ex  a 1 x2 (2)当 设 h(x)  g (x)  ex  2ax h (x)  ex  2a  0 g (x) (1,0) 所以 在单调递增 1g (1)  2a  0, g (0) 1 0 eg (n)  0 n(1,0) 所以存在 ,使得 当 x(1,n), g (x)  0, g(x) 单调递减 x(n,0), g (x)  0, g(x) 单调递增 g(x)  g(0) 1 a  0 当1g(1)  0 又ef (t)  0 ,即 t (1,n) g(t)  0 所以存在 ,使得 x(1,t), f (x) x(t,0), f (x) 当有而单调递增,当 单调递减 x  1, f (x)   f (0)  0 x(t,0), f (x)  0 ,所以当 f (x) (t, 0) 上无零点 (1,t) 所以 在上有唯一零点, f (x) (1,0) 即在上有唯一零点 a  1 f (x) 所以 ,符合题意 a(1,0),(0,) (,1) 各恰有一个零点,求 的取值范围为 所以若 在区间 a【点睛】方法点睛：本题的关键是对 的范围进行合理分类，否定和肯定并用，否定只需 要说明一边不满足即可，肯定要两方面都说明. （二）选考题，共 10 分．请考生在第 22、23 题中任选一题作答．如果多做， 则按所做的第一题计分． [选修 4-4：坐标系与参数方程] x  3 cos2t y  2sint xOy 22. 在直角坐标系 中，曲线 C 的参数方程为 ，（t 为参数），以坐标原点 为极点，x 轴正半轴为极轴建立极坐标系，已知直线 l 的极坐标方程为 3 sin    m  0 ．（1）写出 l 的直角坐标方程； （2）若 l 与 C 有公共点，求 m 的取值范围． 【答案】（1） 3x  y  2m  0 19 12 52 m  （2） 【解析】 【分析】（1）根据极坐标与直角坐标的互化公式处理即可； （2）联立 l 与 C 的方程，采用换元法处理，根据新设 a 的取值范围求解 m 的范围即可. 【小问 1 详解】 3123 sin    m  0 因为 l： ，所以 ， sin   cos  m  0 213 sin  y,  cos  x 又因为 ，所以化简为 ，y  x  m  0 22整理得 l 的直角坐标方程： 【小问 2 详解】 3x  y  2m  0 y  2sint 联立 l 与 C 的方程，即将 ，代入 x  3 cos2t 中，可得3cos2t  2sint  2m  0 ，3x  y  2m  0 所以3(1 2sin2 t)  2sint  2m  0 ，2化简为 ，6sin t  2sint  3 2m  0 2要使 l 与 C 有公共点，则 有解， 2m  6sin t  2sint 3 令sint  a ，则 ，令 f (a)  6a2  2a 3 ，(1≤a≤1) ，a 1,1 1a  对称轴为 ，开口向上， 6f (a)  f (1)  6  2 3  5 所以 ，max 11 2 19 6f (a)min  f ( )  3   ，66 6 19 6 2m  5 所以 19 52 m  m 的取值范围为 .12 [选修 4-5：不等式选讲] 33323. 已知 a，b，c 都是正数，且 ，证明： a2  b2  c2 1 19abc  （1） （2） ；abc1；b  c a c a b 2 abc 【答案】（1）证明见解析 （2）证明见解析 【解析】 【分析】（1）利用三元均值不等式即可证明； （2）利用基本不等式及不等式的性质证明即可． 【小问 1 详解】 333证明：因为 ，b  0 ，，则 ，，，，a  0 c  0 a2  0 b2  0 c2  0 3333333a2  b2  c2 所以  a2 b2 c2 3133111923abc abc  即，所以 ，当且仅当 3 ，即 时取等号． a  b  c  a2  b2  c2 39【小问 2 详解】 证明：因为 所以 ，b  0 ，，a  0 c  0 ，，，b  c  2 bc a  c  2 ac a  b  2 ab 333aaa2 bbb2 ccc2 所以 ，，b  c a  c a  b 2 bc 2 abc 2 ac 2 abc 2 ab 2 abc 333333abca2 b2 c2 a2  b2  c2 2 abc 1b  c a c a b 2 abc 2 abc 2 abc 2 abc 当且仅当 时取等号． a  b  c