2022年高考数学真题（天津自主命题）（解析版）下载

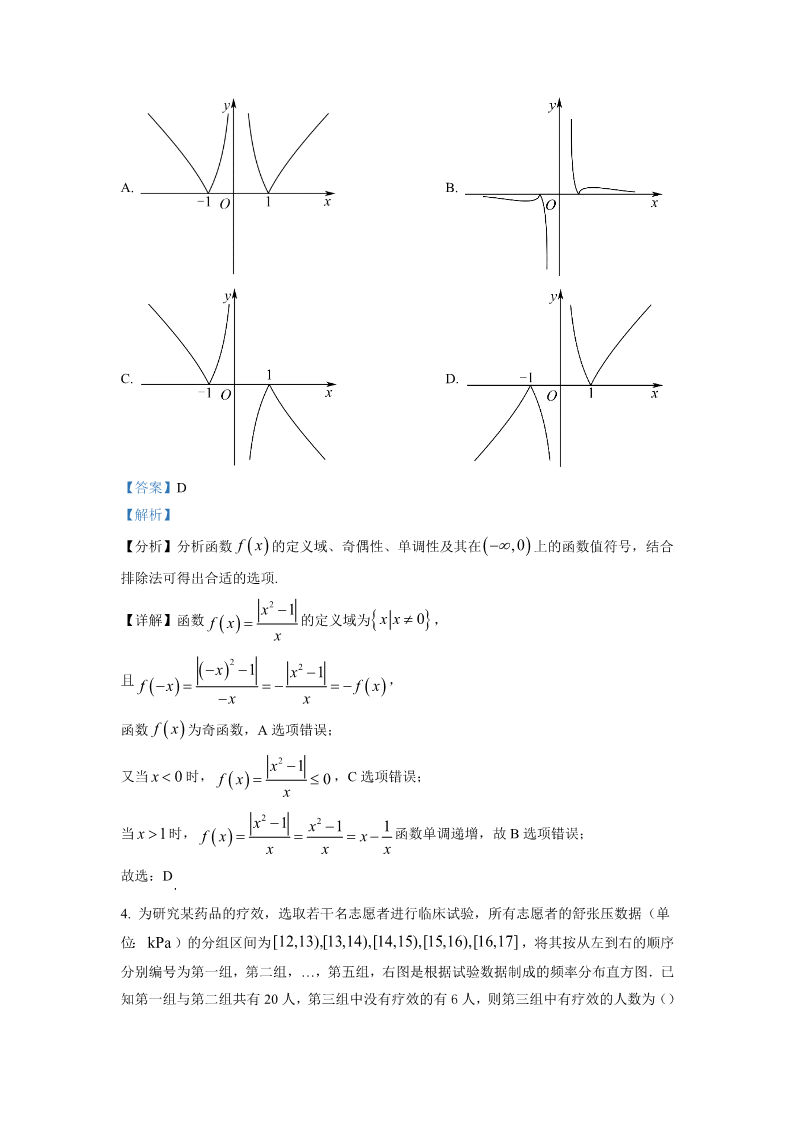
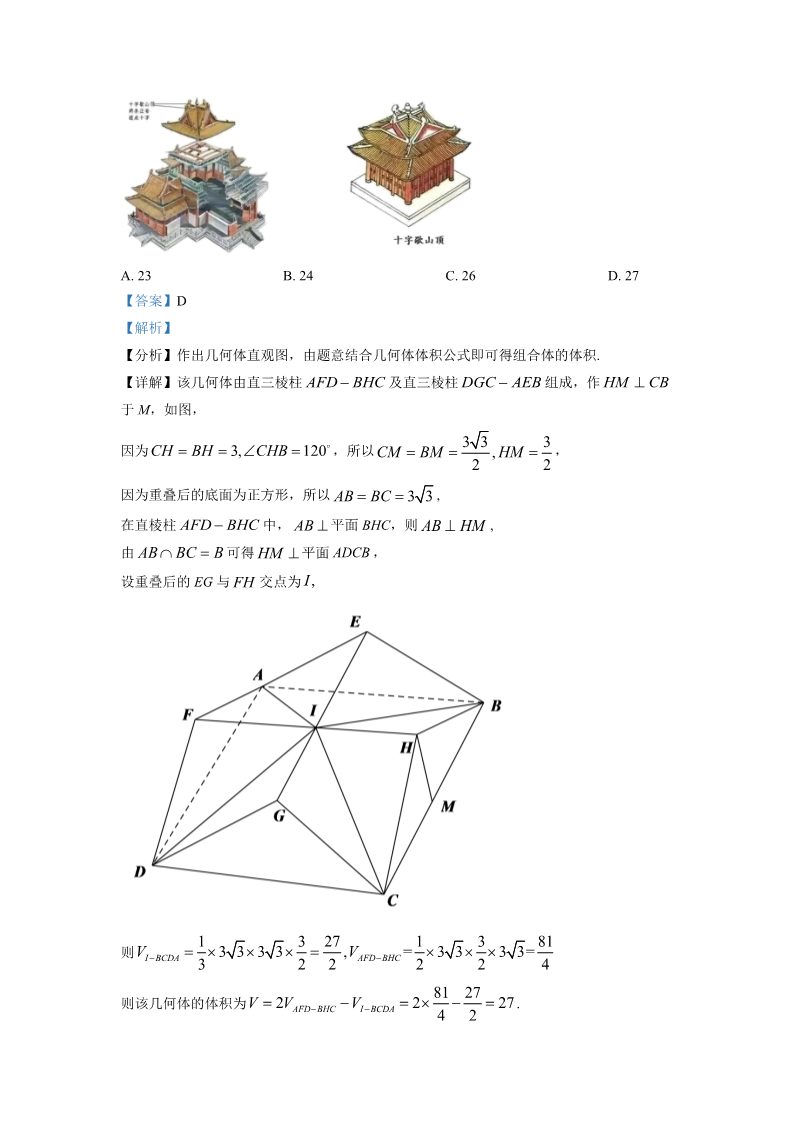
2022 年普通高等学校招生全国统一考试数学（天津卷） 2022．06． 一、选择题：本题共 9 小题，每小题 5 分，共 45 分．在每小题给出的四个选项 中，只有一项是符合题目要求的． A  0,1,2 , B=1,2 U = -2,- 1,0,1,2 A ð B    1. 设全集 {}，集合 ，则 （） U0，1   0,1,2 1,1,2 A. B. C. D. 0,1,1,2 【答案】A 【解析】 ð B A∩ ð B 【分析】先求出 ，再根据交集的定义可求 .UUð B  2,0,1 A ð B  0,1     【详解】 ，故 ，UU故选：A. x2. “ 为整数”是“ A. 充分不必要 C. 充分必要 【答案】A 为整数”的（） 2x 1 B. 必要不充分 D. 既不允分也不必要 【解析】 x【分析】依据充分不必要条件的定义去判定“ 为整数”与“ 为整数”的逻辑关系即可. 2x 1 x【详解】由题意，若 为整数，则 为整数，故充分性成立； 2x 1 1x为整数，但 不为整数，故必要性不成立； x  当时， 2x 1 2x所以“ 为整数”是“ 为整数”的充分不必要条件. 2x 1 故选：A. x2 1 3. 函数 的图像为（） f x   xA. B. C. D. 【答案】D 【解析】 f x ,0 【分析】分析函数  的定义域、奇偶性、单调性及其在 上的函数值符号，结合 排除法可得出合适的选项. x2 1 x x  0 【详解】函数 的定义域为 ，f x   x2x2 1 x 1 且，f x      f x   x xf x 函数  为奇函数，A 选项错误； x2 1 又当 时， ，C 选项错误； x  0 f x    0 xx2 1 x2 1 x1当时， 函数单调递增，故 B 选项错误； x 1 f x    x  xx故选：D .4. 为研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单 [12,13),[13,14),[14,15),[15,16),[16,17] ，将其按从左到右的顺序 位： ）的分组区间为 kPa 分别编号为第一组，第二组，…，第五组，右图是根据试验数据制成的频率分布直方图．已 知第一组与第二组共有 20 人，第三组中没有疗效的有 6人，则第三组中有疗效的人数为（） A. 8 B. 12 C. 16 D. 18 【答案】B 【解析】 【分析】结合已知条件和频率分布直方图求出志愿者的总人数，进而求出第三组的总人数， 从而可以求得结果. 20 【详解】志愿者的总人数为 ＝50， (0.24  0.16)1 所以第三组人数为 50×0.36＝18， 有疗效的人数为 18－6＝12． 故选：B. 0.7 12 3 1  0.7 c  log 5. 已知 ，，，则（） b  a  2   3  a  b  c A. B. C. D. a  c  b b  c  a c  a  b 【答案】C 【解析】 a【分析】利用幂函数、对数函数的单调性结合中间值法可得出 、 、 的大小关系. cb0.7 112 3   0.7 a  b  c .【详解】因为 ，故 2 0  log2 1 log   3  故答案为：C. 2log 3 log 3log 2 log 2 6. 化简 的值为（ ） 4839A. 1 B. 2 C. 4 D. 6 【答案】B 【解析】 【分析】根据对数的性质可求代数式的值. 111 (2 log 3 log 3)(log 2 log 2) 【详解】原式 223323243 log 3 log 2 2 ，2332故选：B x2 y2 7. 已知抛物线 y2  4 5x, F , F2 分别是双曲线 1(a  0,b  0) 的左、右焦点，抛物 1a2 b2 4FF FA  线的准线过双曲线的左焦点 1 ，与双曲线的渐近线交于点 A，若 ，则双曲线的 12标准方程为（） x2 y2  y2 1 x2  1 A. C. B. D. 10 16 y2 x2 x2  1  y2 1 44【答案】C 【解析】 c【分析】由已知可得出 的值，求出点 AF  F F2 A的坐标，分析可得 ，由此可得出关于 11ac、、 的方程组，解出这三个量的值，即可得出双曲线的标准方程. b2F  5,0 1  F2  5,0 【详解】抛物线 的准线方程为 ，则 ，则 、，y  4 5x x  5 c  5 bx  c y  x bc aA c, 不妨设点 A为第二象限内的点，联立 a，可得 ，即点 ，bc y  x  c a4AF  F F △F FA F FA  因为 2 且 ，则 为等腰直角三角形， 111212bc abAF  F F2  2c  2 且，即 ，可得 ，11aba 2 a 1 y2 2c  5 b  2 所以， ，解得 ，因此，双曲线的标准方程为 .x  1 4222c  a  b c  5 故选：C. 8. 如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱 的底面是顶角为 ，腰为3 的等腰三角形，则该几何体的体积为（） 120 A. 23 B. 24 C. 26 D. 27 【答案】D 【解析】 【分析】作出几何体直观图，由题意结合几何体体积公式即可得组合体的体积. 【详解】该几何体由直三棱柱 AFD  BHC 及直三棱柱 DGC  AEB 组成，作 HM  CB 于 M，如图， 3 3 232因为CH  BH  3,CHB 120 ，所以 ，CM  BM  , HM  因为重叠后的底面为正方形，所以 ,AB  BC  3 3 在直棱柱 AFD  BHC 中， 平面 BHC，则 ,AB  AB  HM ADCB ，由可得 平面 AB  BC  B HM  I, 交点为 设重叠后的 EG 与 FH 1327 1381 4V 3 33 3 ,VAFDBHC = 3 3 3 3= 则I BCDA 3222281 27 V  2V VI BCDA  2  27 则该几何体的体积为 .AFDBHC 42故选：D. 1f (x)  sin 2x 9. 已知 f (x) ，关于该函数有下列四个说法： ；22π ①的最小正周期为 π π f (x) [ , ] ②在上单调递增； 4 4 π π 33f (x) x , ,③当 时， 的取值范围为 ；6 3 441ππf (x) g(x)  sin(2x  ) ④的图象可由 的图象向左平移 个单位长度得到． 824以上四个说法中，正确的个数为（） A. B. C. D. 3124【答案】A 【解析】 【分析】根据三角函数的图象与性质，以及变换法则即可判断各说法的真假． 12π f (x) 的T   π ，①不正确； f (x)  sin 2x 【详解】因为 ，所以 最小正周期为 22π π π π 1π π f (x) t  2x ,  , [ , ] y  sint 令，而 在上递增，所以 在上单调递增，② ，③不正确； 4 4 2 2 2 2 2π 2π 33 1 ,t  2x , sint   ,1 f x  正确；因为 ，，所以   3 3 4 2 21π1π  1πf (x) g(x)  sin(2x  )  sin 2 x  g(x)  sin(2x  ) 由于 ，所以 的图象可由 242824π的图象向右平移 个单位长度得到，④不正确． 8故选：A． 第 II 卷 二、填空题：本大题共 6 小题，每小题 5 分，共 30 分．试题中包含两个空的， 答对 1 个的给 3 分，全部答对的给 5 分． 113i 1+2i 10. 已知 是虚数单位，化简 的结果为_______． i【答案】 【解析】 ## 15i 5i 1 【分析】根据复数代数形式的运算法则即可解出． 113i 1 2i  113i 1+2i 11 6  25i 15i ．【详解】 1+2i 1 2i 5 故答案为： ．15i 53×2 11. 的展开式中的常数项为______. x  15 【答案】 【解析】 555r 23×2 Tr1  C5r 3r  x 【分析】由题意结合二项式定理可得 的展开式的通项为 ，x  55r  0 令，代入即可得解. 25r55r 25r 3×2 3×2 【详解】由题意 的展开式的通项为 ，x  Tr1  Cr  x C5r 3r  x 555r  0 Cr 3r  C1 3 15 令即，则 ，r 1 55253×2 的15 .所以 展开式中的常数项为 x  15 故答案为： .【点睛】本题考查了二项式定理的应用，考查了运算求解能力，属于基础题. 22m相交所得的弦长为 ，则 m  x  y  m  0 m  0 12. 若直线 _____． 与圆 x 1  y 1  3 【答案】 【解析】 2mm【分析】计算出圆心到直线的距离，利用勾股定理可得出关于 的等式，即可解得 的值. 221,1 【详解】圆 圆心到直线 的圆心坐标为 ，半径为 ，3x 1  y 1  3 11 m mx  y  m  0 m  0 的距离为 ，222 2mm由勾股定理可得 ，因为 m  0，解得 m  2 . 3 22故答案为： .213. 52 张扑克牌，没有大小王，无放回地抽取两次，则两次都抽到 A 的概率为 ____________；已知第一次抽到的是 A，则第二次抽取 A 的概率为____________ 11【答案】 【解析】 ①. ②. 221 17 【分析】由题意结合概率的乘法公式可得两次都抽到 A 的概率，再由条件概率的公式即可 求得在第一次抽到 A 的条件下，第二次抽到 A 的概率. 【详解】由题意，设第一次抽到 A 的事件为 B,第二次抽到 A 的事件为 C, 1P BC 431411221 1P BC  , P(B)  , P C| B  则.52 51221 52 13 P B   17 13 11故答案为： ；221 17 .    ，试用  为14. 在 中， ，D 是 AC 中点， 表示 ABC CA  a,CB  b a,b CB  2BE DE   ACB ___________，若 ，则 的最大值为____________ AB  DE 3216b  a 【答案】 【解析】 ①. ②. 2  a,b  【分析】法一：根据向量的减法以及向量的数乘即可表示出 ，以 为基底，表示出 DE   2 2   ，由 可得 ，再根据向量夹角公式以及基本不等式即可求 AB  DE AB, DE 3b  a  4ba 出． E(0,0), B(1,0),C(3,0), A(x, y) 法二：以点 为原点建立平面直角坐标系，设 E，由 AB  DE 可得点 A的轨迹为以 为圆心，以 为半径的圆，方程为 (x 1)2  y2  4，即 C M (1,0) r  2 M 可根据几何性质可知，当且仅当 【详解】方法一： 与相切时， 最大，即求出． CA   ，         31DE=CE CD  b  a ，AB  CB CA  b  a, AB  DE  (3b  a)(b  a)  0 22  2 3a b     ab 3b2  a2 32 2    cosACB      ，当且仅当 3b  a  4ab 2a b 4 a b 4 a b 6a  3 b ACB(0, ] 时取等号，而 0  ACB  π ，所以 ．；3216b  a 故答案为： ．2方法二：如图所示，建立坐标系：   x  3 2yE(0,0), B(1,0),C(3,0), A(x, y) DE  ( , ), AB  (1 x,y) ，，2  x  3 2y2  (x 1)2  y2  4 ，所以点  0 M (1,0) A的轨迹是以 DE  AB  ( )(x 1)  2M C 最大，此时 为圆心，以 为半径的圆，当且仅当 与相切时， CA r  2 r2416sinC   ,C  ．CM 2316b  a 故答案为： ；．22f x min x  2, x2  ax  3a 5 f x   至少有 3 15. 设 ，对任意实数 x，记   ．若 aR a个零点，则实数 的取值范围为______. 【答案】 a 10 【解析】 g x  x2  ax  3a 5 h x  x  2   ，分析可知函数  至少有一个零点， g x 【分析】设   ，aa可得出 ，求出的取值范围，然后对实数 的取值范围进行分类讨论，根据题意可得   0 aa出关于实数 的不等式，综合可求得实数 的取值范围. g x  x2  ax  3a 5 h x  x  2 x  2  0 【详解】设   ，  g x ，由 可得 .x  2 2f x 要使得函数  至少有 个零点，则函数  至少有一个零点，则 ，3  a 12a  20  0 解得 或a  2 a 10 .g x  x2  2x 1 g x h x a  2 ①当 时，   ，作出函数   、 的图象如下图所示： f x 此时函数  只有两个零点，不合乎题意； g x x x x 2  2  x②当 时，设函数  的两个零点分别为 、，a  2 11f x x  2 要使得函数  至少有 个零点，则 ，32a 2 2所以， ，解得 ；a g 2  4  5a 5  0 g x  x2 10x  25 g x h x 、③当 时，   ，作出函数    的图象如下图所示： a 10 f x 由图可知，函数  的零点个数为 ，合乎题意； 3g x xx x x ④当 时，设函数  的两个零点分别为 、4  4  ，a 10 33f x x  2 要使得函数  至少有 个零点，则 ，33a 2 2a  4 ，此时 可得 ，解得 .a 10 g 2  4  a 5  0   a综上所述，实数 的取值范围是 10, .10, .故答案为： 【点睛】方法点睛：已知函数有零点（方程有根）求参数值（取值范围）常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决； （3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画 出函数的图象，利用数形结合的方法求解. 三、解答题：本大题共 5 小题，共 75 分，解答应写出文字说明，证明过程或演 算步骤． 1a  6,b  2c,cos A   16. 在 中，角 A、B、C 的对边分别为 a，b，c.已知 .ABC 4c（1）求 的值； （2）求 （3）求 的值； sin B sin(2A B) 的值. 【答案】（1） c 1 10 4（2） sin B  10 8（3） sin(2A B)  【解析】 【分析】（1）根据余弦定理 222以及 解方程组即可求出； b  2c a  b  c  2bccos A （2）由（1）可求出 ，再根据正弦定理即可解出； b  2 sin 2A,cos2A （3）先根据二倍角公式求出 【小问 1 详解】 ，再根据两角差的正弦公式即可求出． 16  b2  c2  bc 222因为 ，即 ．，而 ，代入得 b  2c a  b  c  2bccos A 26  4c2  c2  c 2 ，解得： c 1 【小问 2 详解】 由（1）可求出 ab15 42，而 ，所以 ，又 ，b  2 0  A  π sin A  1 cos A  sin A sin B 15 2 bsin A 10 ．所以 4sin B  a46【小问 3 详解】 ππ115 2cos A    A  π 0  B  因为 ，所以 ，故 ，又 ，所以 sin A  1 cos A  42241415 15 sin 2A  2sin Acos A  2    ，481710 cos2A  2cos2 A1 2 1  ，而 ，所以 sin B  16 846cos B  1sin2 B  ，415 86710 410 ．8sin(2A B)  sin 2Acos B  cos2Asin B     故48ABC  A B C AA  AB  AC  2, AA  AB, AC  AB A B ，D 为 1 的 117. 直三棱柱 1 中， 1111AA 中点，E 为 的中点，F 为 的中点． CD 1（1）求证： 平面 ；EF// ABC CC D （2）求直线 BE 与平面 所成角的正弦值； 1ACD CC D 所成二面角的余弦值． 1（3）求平面 与平面 1【答案】（1）证明见解析 4（2） 510 （3） 10 【解析】 yxzAA AA BAC 、 、1 所在直线分别为 、 、 轴建立空 1 1 11 【分析】（1）以点 1 为坐标原点， 间直角坐标系，利用空间向量法可证得结论成立； CC D （2）利用空间向量法可求得直线 BE 与平面 夹角的正弦值； 1ACD CC D 夹角的余弦值. 1（3）利用空间向量法可求得平面 【小问 1 详解】 与平面 1ABC  A B C AA  A B CAC  A B 1 ，且 AC  AB ，则 证明：在直三棱柱 1 中， 平面 11111111 1 y1 所在直线分别为 、 、 轴建立如下图所示的空 xzA以点 1 为坐标原点， A AA BAC 、、1111间直角坐标系， A 2,0,0 B 2,2,0 C 2,0,2 A 0,0,0 1  B 0,0,2 1  C 0,0,2 1  则、、、、、、 11F 1, ,1 D 0,1,0 E 1,0,0 EF  0, ,1 、、，则 ，22 m  1,0,0     ，易知平面 的一个法向量为 ，故 ，则 ，故 ABC EF m  0 EF  m 平面 平面 .ABC EF  【小问 2 详解】 ABC EF//    EB  1,2,0 C C  2,0,0 C D  0,1,2 解： ，，，11 u C C  2x  0 11CC D  u  x , y , z 设平面 的法向量为 ，则 ，1  111u C D  y  2z  0 111    cos  EB,u  EBu 4  y  2 u  0,2,1 取，可得 ，.15EB  u 4CC D 因此，直线 BE 与平面 【小问 3 详解】 夹角的正弦值为 . 51  AC  2,0,2 A D  0,1,0 解： ，，11 v  AC  2x  2z  0 122ACD  v  x , y , z 设平面 的法向量为 ，则 ，2  122v  A D  y  0 12    u v 110 cos  u,v        x 1 v  1,0,1 取，可得 ，则 ，．210 5  2 u  v 10 10 ACD CC D 夹角的余弦值为 1因此，平面 与平面 .1a  nb  是等比数列，且 n1a  b  a b  a b 1 18. 设 是等差数列， 12233ab（1）求  与 的通项公式； nnaSSn1  an1 b  S bn1  Snbn ；（2）设 的前 n 项和为 n ，求证： nn1 n2n kak1  (1) ak bk （3）求 ． k1 a  2n 1,b  2n1 【答案】（1） nn(3n1)4n2 16 （2）证明见解析（3） 9【解析】 【分析】（1）利用等差等比数列的通项公式进行基本量运算即可得解； （2）由等比数列的性质及通项与前 n 项和的关系结合分析法即可得证； 2k1 b2k1  a2k1  (1)2k a2k b2k a2k  (1) a（3）先求得 ，进而由并项求和可得 2k1 nT  k 4k1 ，再结合错位相减法可得解. nk1 【小问 1 详解】 a 1 (n 1)d,b  qn1 公比为 q，则 bna设 公差为 d，  ，nnn1 d  q 1 a b  a b 1  d  q  2 d  q  0 （由可得 舍去）， 22331 2d  q2 1 a  2n 1,b  2n1 所以 ；nn【小问 2 详解】 b 2b  0, (Sn1  an1)bn  Sn1bn1  Snbn 证明：因为 所以要证 ，n1 n(Sn1  an1)bn  Sn1 2bn  Snb Sn1  an1  2Sn1  Sn 即证 即证 n ，即证 ，an1  Sn1  Sn ，an1  Sn1  S (Sn1  an1)bn  Sn1 bn1  Sn bn 而n 显然成立，所以 ；【小问 3 详解】 2k1 b2k1  a2k1  (1)2k a2k b2k a2k  (1) 因为 a2k1  (4k 1 4k 3)22k1 [4k 1 (4k 1)]22k  k 4k1 ，2n nkak1  (1) ak bk [(a  (1)2k1a2k1)b2k1  (a2k1  (1)2k a2k )b2k ] 所以  2k k1 k1 nk 4k1 ，k1 nT  k 4k1 设nk1 T 142  243  344  n4n1 所以 ，n4T 143  244  345  n4n2 则，n42 (1 4n ) 1 4 2343Tn  4  4  4  4n1  n4n2  n4n2 作差得 13n 4n2 16 ，3(3n 1)4n2 16 所以 所以 ，Tn  92n (3n1)4n2 16 kak1  (1) ak bk  . 9k1 x2 y2 BF AB 319. 椭圆 的右焦点为F、右顶点为A，上顶点为B，且满足 ．1 a  b  0 a2 b2 2e（1）求椭圆的离心率 ； （2）直线 l 与椭圆有唯一公共点 M，与 y 轴相交于 N（N 异于 M）．记 O 为坐标原点，若 OM  ON ，且 的面积为 ，求椭圆的标准方程． 3OMN 63【答案】（1） e  x2 y2 （2） 1 62【解析】 a【分析】（1）根据已知条件可得出关于 、 的等量关系，由此可求得该椭圆的离心率的值； b（2）由（1）可知椭圆的方程为 x2  3y2  a2 ，设直线 的方程为 y  kx  m ll，将直线 的方 3m2  a2 1 3k2 M，求出点 的坐标，利用三角形的 程与椭圆方程联立，由 可得出   0 面积公式以及已知条件可求得 2 的值，即可得出椭圆的方程. a【小问 1 详解】 b2  c2 b2  a2 a3BF  4a2  3 b2  a2  a2  3b2 解： ，b2  a2 AB 2ca2 b2 6离心率为 .e  aa2 3【小问 2 详解】 解：由（1）可知椭圆的方程为 x2  3y2  a2 y  kx  m ，ll易知直线 的斜率存在，设直线 的方程为 ，y  kx  m x2  3y2  a2 1 3k2 x2  6kmx  3m2  a2  0 联立 得，  36k2m2  4 1 3k2 3m2  a2  0  3m2  a2 1 3k2 由，①  3km 3k2 1 m1 3k2 xM   y  kx  m  ，，MMm2 9k2 1 ，② m2  OM  ON 由由可得 23k2 1 3km 1 3k2 1SOMN  3 可得 ，③ m   3 2×2 y2 1k2  22联立①②③可得 ，，，故椭圆的标准方程为 ．a  6 1 m  4 362f x ex  asin x, g x  b x 20. 已知 ，函数 a，bR     y  f x 0, f 0 （1）求函数   在  处的切线方程； y  f x   y  g x （2）若 （i）当 和 有公共点， 时，求 的取值范围； ba  0 22（ii）求证： ．a  b  e y  (1 a)x 1 【答案】（1） b 2e, （2）（i） ；（ii）证明见解析 【解析】 f (0) 【分析】（1）求出 可求切线方程； 2有公共点即为 s t et bt,t  0 在y  f (x) y  g(x) （2）（i）当 时，曲线 和a  0   0, .上有零点，求导后分类讨论结合零点存在定理可求 b[ 2e,) asin x  b x  ex0  0 y  f (x) y  g(x) （ii）曲线 和有公共点即 ，利用点到直线的距离 00ex 0e2x sin2 x  x a2  b2  得到 ，利用导数可证 ，从而可得不等式成立. >e sin2 x0  x0 【小问 1 详解】 xf (0) 1 a f (0) 1 f (x)  e  acos x ，故 ，而 ，f (x) (0, f (0)) y  1 a x 0 1 y  1 a x1 曲线 在点 处的切线方程为  即.【小问 2 详解】 （i）当 时， a  0 xy  f (x) y  g(x) 因为曲线 和有公共点，故 有解， e  b x t2 0, 设，故 2 ，故 在上有解， t  x x  t e  bt 2s t 0, 设而若若s t et bt,t  0 ，故   在上有零点，   t2 s t  2te b,t  0 ，  2，则 s t et  0 恒成立，此时   在上无零点， s t 0, b  0   s t  0 ，则   0, s t 0, b  0 在上恒成立，故   在上为增函数， s 0 1 0 s t  s 0 1 s t ，故   0, 而故设  ，    在上无零点， b  0 ，22t2 u t  2tet b,t  0，则 ，u t  2  4t e  0     u t   0, 故而在上为增函数， 2u 0  b  0 u b  b 2eb 1  0   u t ，  ，上存在唯一零点 0, t，0故且故  在0  t  t 0  t  t s t u t  0 t  t u t  0 0 时，   ；0 时，   ；s t  0 t  t s t  0 0 时，   ；0 时，   ；0,t t , 所以   在0  上为减函数，在 上为增函数， 0s t  min  s t   故，0t02 s t 因为   0, s t 0 在上有零点，故   ，故 ，e bt0  0 0t02 t02 t02 22而，故 即，2t0e b  0 e  2t0 e  0 t0  22t2 2设故而v t 2tet ,t  0，则 ，v t  2  4t e  0     v t   0, 在上为增函数， 1t02 ，故 .b  2t0e b  2e2  2e y  f (x) y  g(x) （ii）因为曲线 和有公共点， xx有解 0 ，其中 x  0 所以 ，e  asin x  b x 0x  0 x  0 .若故，则 ，该式不成立，故 1 a0  b0 00asin x  b x  ex0  0 asin x  b x  ex0  0 ，考虑直线 ，0000asin x  b x  ex0  0 a2  b2 a,b 表示原点与直线 上的动点 之间的距离， 00ex e2x 00a2  b2  a2  b2  故，所以 ，sin2 x0  x0 sin2 x0  x0 sin x  x 下证：对任意 ，总有 ，x  0 22sin x  x x  sin x 1 x 证明：当 时，有 ，故 成立. 20  x  当时，即证 ，sin x  x p x  sin x  x   p x cos x 1 0 ，则   设（不恒为零）， p x  p 0  0 p x  sin x  x   0,     故在上为减函数，故 即成立. sin  x sin x  x 综上， 成立. x下证：当 时， 恒成立， x  0 e  x 1 xq x  ex 1 x, x  0 q x e 1 0   ，则   ，xq x   0, q x  q 0  0 故在上为增函数，故   0,   即恒成立. e  x 1 e2x sin2 x  x 2x1 2下证： 即证： 在上恒成立，即证： ，>e e sin x  x 22，即证： ，2x 11 sin x  x x  sin x x  sin x  sin2 x 2而，故 成立. x  sin x ex sin2 x0  x0 022 e 故，即 成立. a  b  e 【点睛】思路点睛：导数背景下零点问题，注意利用函数的单调性结合零点存在定理来处理， 而多变量的不等式的成立问题，注意从几何意义取构建不等式关系，再利用分析法来证明目 标不等式.