
 2019年普通高等学校招生全国统一考试(浙江卷)数学 参考公式: P(A B) P(A) P(B) P(AB) P(A)P(B) A, B A, B 若事件 若事件 若事件 互斥,则 柱体的体积公式 V Sh 相互独立,则 其中 表示柱体的底面积, 表示柱体的高 hSp在一次试验中发生的概率是 ,则 nA次1V Sh 3锥体的体积公式 独立重复试验中事件 恰好发生次的概率 kA其中 表示锥体的底面积, Sh表示锥体的高 P (k) Cnk pk (1 p)nk (k 0,1,2,,n) n2球的表面积公式 S 4 R 台体的体积公式 4V R3 球的体积公式 3S , S 其中 分别表示台体的上、下底面积, 表 h12其中 表示球的半径 R示台体的高 选择题部分(共 40分) 一、选择题:本大题共 10小题,每小题 4分,共 40分,在每小题给出的四个选项中,只有一 项是符合题目要求的. U 1,0,1,2,3 A 0,1,2 B 1,0,1 1.已知全集 ,集合 ,,则(∁UA)∩B=( ) 1 0,1 A. C. B. D. 1,2,3 1,0,1,3 x y 0 2.渐近线方程为 的双曲线的离心率是( )2A. B. 1 D. 2 2C. 2x 3y 4 0 3x y 4 0 x y 0 x, y z 3x 2y 3.若实数 满足约束条件 ,则 的最大值是( )A. B. 1 1 C 10 .D. 12 4.祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容易”称为祖暅原理,利用该原理可 V Sh 以得到柱体体积公式 该柱体的体积是( ,其中 是柱体的底面积, 是柱体的高,若某柱体的三视图如图所示,则 hS柱体 )A. 158 C. 182 B. 162 D. 32 a 0,b 0 5.若 ,则“ ”是 “ ”的( )a b 4 ab 4 A. 充分不必要条件 C. 充分必要条件 B. 必要不充分条件 D. 既不充分也不必要条件 112y , y log x (a 0 a 0) 的6.在同一直角坐标系中,函数 且图象可能是( )a ax A. B. C. D. 7.设 ,则随机变量 的分布列是: X0 a 1 a0,1 则当 在内增大时( )D X D X 减小 A. C. 增大 B. D. D X D X 先增大后减小 先减小后增大 V ABC 的底面是正三角形,侧棱长均相等, 8.设三棱锥 是棱 上的点(不含端点),记直线 与VA PPB 的平面角为 ,则( 所成角为 ,二面角 所成角为,直线 直线 与平面 PB )AC ABC P AC B , , , A. C. B. D. , x, x 0 a,b R f (x) y f (x) ax b 9.已知 ,函数 ,若函数 恰有三个零点,则 1 1×3 (a 1)x2 ax, x 0 32()a 1,b 0 a 1,b 0 a 1,b 0 A. B. D. C. a 1,b0 a,b R , 则( )2a10.设 ,数列 中,a =a,a =a +b, nN 1n+1 nn,11b ,a 10 b ,a 10 A. 当 C. 当 B. 当 D. 当 10 10 24b 2,a 10 b 4,a 10 10 10 非选择题部分(共 110分) 二、填空题:本大题共 7小题,多空题每题 6分,单空题每题 4分,共 36分 1i( 为虚数单位),则 | z | z 11.复数 ________. 1 i m A(2,1) ,则 _____, 2x y 3 0 与圆相切于点 Cr,半径长是 .若直线 (0,m) 12.已知圆 的圆心坐标是 ______. r 13.在二项式 9 的展开式中,常数项是________;系数为有理数的项的个数是_______. ( 2 x) 14.在 中, ,,,点 在线段 上,若BDC 45,则 VABC ABC 90 BC 3 AC BD ____; AB 4 DcosABD ________. x2 y2 在椭圆上且在 x轴的上方,若线段 15.已知椭圆 的左焦点为 ,点 F的中点在以原点 为圆 OPF 1 P95OF 心, 为半径的圆上,则直线 的斜率是_______. PF 233a,则实数 的最大值是 | f (t 2) f (t) | 16.已知 ,函数 ,若存在 ,使得 a R f (x) ax x t R ____. (i 1,2,3,4,5,6) 17.已知正方形 的边长为 1,当每个 取遍 时, ABCD i 的最小值是________;最大值是_______. | 1 AB 2 BC 3CD 4 DA 5 AC 6 BD | 三、解答题:本大题共 5小题,共 74分,解答应写出文字说明、证明过程或演算步骤. f (x) sinx, xR 18.设函数 . [0,2), f (x ) (1)已知 (2)求函数 函数 是偶函数,求 的值; 12 y [ f (x )]2 [ f (x )]2 的值域. 4ABC A B C 1 ,平面 A AC C 19.如图,已知三棱柱 平面 ,,ABC ABC 90 1111BAC 30, A A AC AC, E, F AC, A B 1 的中点. 1分别是 11(1)证明: (2)求直线 ;EF BC A BC 与平面 所成角的余弦值. EF 1n{a } Sa 4 a S ,b,数列 满足:对每 n的前20.设等差数列 项和为 , nn343nN, Sn bn , Sn1 bn , Sn2 b n 成等比数列. {a },{b } (1)求数列 的通项公式; nnan ,nN, C (2)记 证明: C1 C2 + Cn 2 n,nN . n2bn 2A,B ,点 为焦点,过点 的直线交抛物线于 两点,点 21.如图,已知点 F(1,0)为抛物线 y 2px( p 0) CFFxx轴于点 ,且 在点 右侧.记 QQ在抛物线上,使得 的重心 在轴上,直线 交VABC GFAC S , S △AFG,△CQG 的面积为 .21p(1)求 的值及抛物线的标准方程; S1 (2)求 的最小值及此时点 的坐标. GS2 22.已知实数 a 0 ,设函数 f (x)=aln x x 1, x 0. 3f (x) a (1)当 时,求函数 的单调区间; 41xa求 的取值范围. x[ ,) (2)对任意 均有 f (x) ,e2 2a 注: 为自然对数的底数. e 2.71828… 2019年普通高等学校招生全国统一考试(浙江卷)数学 参考公式: P(A B) P(A) P(B) P(AB) P(A)P(B) A, B A, B 若事件 若事件 若事件 互斥,则 柱体的体积公式 V Sh 相互独立,则 其中 表示柱体的底面积, 表示柱体的高 hSp,则 n 次 A在一次试验中发生的概率是 1V Sh 3锥体的体积公式 独立重复试验中事件 恰好发生次的概率 kA其中 S表示锥体的底面积, 表示锥体的高 hP (k) Cnk pk (1 p)nk (k 0,1,2,,n) n2球的表面积公式 S 4 R 台体的体积公式 4V R3 球的体积公式 3S , S 其中 分别表示台体的上、下底面积, 表 h12其中 表示球的半径 R示台体的高 选择题部分(共 40分) 一、选择题:本大题共 10小题,每小题 4分,共 40分,在每小题给出的四个选项中,只有一 项是符合题目要求的. U 1,0,1,2,3 A 0,1,2 B 1,0,1 1.已知全集 ,集合 ,,则(∁UA)∩B=( ) 1 A. C. B. D. 0 , 1 1,2,3 1,0,1,3 【答案】A 【解析】 【分析】 本题借根据交集、补集的定义可得.容易题,注重了基础知识、基本计算能力的考查. C A={1,3} C A B {1} 【详解】 ,则 UU【点睛】易于理解集补集的概念、交集概念有误. x y 0 2.渐近线方程为 的双曲线的离心率是( )2A. B. 1 D. 2 2C. 2【答案】C 【解析】 【分析】 .,进一步可得离心率 容易题,注重了双曲线基础知识、基本 本题根据双曲线的渐近线方程可求得 a b 1 计算能力的考查. 22x y 0 【详解】因为双曲线的渐近线为 ,所以 a=b=1,则 ,双曲线的离心率 c a b 2 ce 2 .a【点睛】理解概念,准确计算,是解答此类问题的基本要求.部分考生易出现理解性错误. x 3y 4 0 3x y 4 0 x y 0 x,y 3.若实数 满足约束条件 z 3x 2y ,则 的最大值是( )A. B. 1 1 C. 10 D. 12 【答案】C 【解析】 【分析】 本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知 识、基本技能的考查. (-1,1),(1,-1),(2,2) 【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以 为顶点的三角形 z=3x+2y (2,2) z=3x+2y 时, 取最大值 区域(包含边界),由图易得当目标函数 经过平面区域的点 zmax 32 22 10 .【点睛】解答此类问题,要求作图要准确,观察要仔细.往往由于由于作图欠准确而影响答案的准确程度, 也有可能在解方程组的过程中出错. 4.祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容易”称为祖暅原理,利用该原理可 V Sh 以得到柱体体积公式 ,其中 是柱体的底面积,是柱体的高,若某柱体的三视图如图所示,则该 S柱体 柱体的体积是( )A. 158 B. 162 D. 32 C. 182 【答案】B 【解析】 【分析】 本题首先根据三视图,还原得到几何体—棱柱,根据题目给定的数据,计算几何体的体积.常规题目.难度不 大,注重了基础知识、视图用图能力、基本计算能力的考查. 【详解】由三视图得该棱柱的高为 6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为 4,下 底 为6 , 高 为3 , 另 一 个 的 上 底 为2 , 下 底 为6 , 高 为3 , 则 该 棱 柱 的 体 积 为 2 6 24 6 23 3 6 162 .【点睛】易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心算. a 0,b 0 5.若 ,则“ ”是 “ ”的( )a b 4 ab 4 A. 充分不必要条件 C. 充分必要条件 【答案】A B. 必要不充分条件 D. 既不充分也不必要条件 【解析】 【分析】 a,b 的本题根据基本不等式,结合选项,判断得出充分性成立,利用“特殊值法”,通过特取 值,推出矛盾, .确定必要性不成立 题目有一定难度,注重重要知识、基础知识、逻辑推理能力的考查. a > 0, b > 0 【详解】当 性成立;当 时, ,则当 时,有 ,解得 ,充分 a b 4 ab 4 a b 2 ab 2 ab a b 4 a=1, b=4 时,满足 ,但此时 a+b=5>4 ,必要性不成立,综上所述,“ ”是 ab 4 a b 4 “”的充分不必要条件. ab 4 【点睛】易出现的错误有,一是基本不等式掌握不熟,导致判断失误;二是不能灵活的应用“赋值法”,通 a,b 过特取 的值,从假设情况下推出合理结果或矛盾结果. 112y , y log x (a 0 a 0) 6.在同一直角坐标系中,函数 且的图象可能是( )a ax A. B. C. D. 【答案】D 【解析】 【分析】 a本题通过讨论 的不同取值情况,分别讨论本题指数函数、对数函数的图象和,结合选项,判断得出正确结 论.题目不难,注重重要知识、基础知识、逻辑推理能力的考查. 1ax 时,函数 y ax 过定点 且单调递减,则函数 过定点 (0,1) (0,1) 且单调递增,函 y 【详解】当 0 a 1 11y ax y log x (0,1) 且单调递 ( ,0) 数过定点 且单调递减,D 选项符合;当 时,函数 过定点 a 1 a 2211ax 12(0,1) y log x y ( ,0) 增,则函数 过定点 且单调递减,函数 过定点 且单调递增,各选项均不 a 2符合.综上,选 D. 【点睛】易出现的错误有,一是指数函数、对数函数的图象和性质掌握不熟,导致判断失误;二是不能通 a过讨论 的不同取值范围,认识函数的单调性. 7.设 ,则随机变量 的分布列是: X0 a 1 a0,1 则当 在内增大时( )D X D X 减小 A. C. 增大 B. D. D X D X 先增大后减小 先减小后增大 【答案】D 【解析】 【分析】 aa研究方差随 变化的增大或减小规律,常用方法就是将方差用参数 表示,应用函数知识求解本题根据方 .a差与期望的关系,将方差表示为 的二次函数,二测函数的图象和性质解题题目有一定综合性,注重重要 .知识、基础知识、运算求解能力的考查. 1 a 3E(X ) 【详解】方法 1:由分布列得 ,则 22 0 2 a 2 1 1 a 311 a 311 a 31291216a(0,1) 内增大时, ,则当 在D(X ) a 333D(X ) 先减小后增大. 2a2 1 (a 1)2 2a2 2a 2 D(X ) E X2 E(X ) 0 2913a 方法 2:则 故选 D. 339924【点睛】易出现的错误有,一是数学期望、方差以及二者之间的关系掌握不熟,无从着手;二是计算能力 差,不能正确得到二次函数表达式. V ABC 8.设三棱锥 的底面是正三角形,侧棱长均相等, 是棱VA 上的点(不含端点),记直线 与直 PPB 的平面角为 ,则( 所成角为 ,二面角 所成角为,直线 线与平面 PB )AC ABC P AC B , , , A. B. D. , C. 【答案】B 【解析】 【分析】 本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的 计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则 可事倍功半. AC VABC O的投影为 ,则 AO P在底面投影 在线段 上,过 【详解】方法 1:如图 为中点, 在底面 GDD作DE 垂直 ,易得 PE / /VG ,过 P作交PF // AC VG 于,过 作,交 于,则 DH / /AC BG AE FDHPF EG DH BD BPF, PBD, PED cos cos , 则 , 即 ,PB PB PB PB PD PD y tan tan ,即 ,综上所述,答案为 B. ED BD 的平面角为 (显然 方法 2:由最小角定理 ,记 )V AB C 由最大角定理 ,故选 B. V ABC 法 2:(特殊位置)取 为正四面体, 为中点,易得 VA P333 622 2 ,故选 B. cos sin ,sin , sin 633【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解 法. x, x 0 a,b R f (x) y f (x) ax b 9.已知 ,函数 ,若函数 恰有三个零点,则 1 1×3 (a 1)x2 ax, x 0 32()a 1,b 0 a1,b0 A. B. D. a 1,b 0 C. a 1,b0 【答案】D 【解析】 【分析】 本题综合性较强,注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函 数方程的方法较为灵活,通常需要结合函数的图象加以分析. y f (x) y ax b ,有三个交点. 【详解】原题可转化为 与f (0) 0, f (0) a 当时, f (x) x2 (a 1)x a (x a)(x 1) ,且 ,则 BC AP y f (x) y ax b 不可能有三个交点(实际上有一个),排除 A,B (1)当 时,如图 与a 1 y f (x) y ax b (2)当 时,分三种情况,如图 a1 与若有三个交点,则 ,答案选 D b 0 下面证明: a 1时, 时11F(x) f (x) ax b x3 (a 1)x2 b ,F (x) x2 (a 1)x x(x (a 1)) ,则 BC AP 3210 b (a 1)3 F(0) > 0 ,F(a+1)<0 ,才能保证至少有两个零点,即 ,若另一零点在 0 6a,b 【点睛】遇到此类问题,不少考生会一筹莫展.由于方程中涉及 两个参数,故按“一元化”想法,逐步 .分类讨论,这一过程中有可能分类不全面、不彻底 . , ,则( )2aa,b R ,数列 10.设 中,a1=a,an+1=a +b, nnN n11b ,a 10 b ,a 10 A. 当 B. 当 10 10 24b 2,a 10 b 4,a 10 C. 当 D. 当 10 10 【答案】A 【解析】 【分析】 本题综合性较强,注重重要知识、基础知识、运算求解能力、分类讨论思想的考查.本题从确定不动点出发, 通过研究选项得解. 21121122a a 0, ,an 【详解】选项 B:不动点满足 时,如图,若 ,x x x 0 124排除 1212a如图,若 为不动点 a 则n2ax 1 1292a 2 10 选项 C:不动点满足 排除 ,不动点为 ,令 ,则 ,a 2 x x 2 x 0 n2421217 17 1217 2122选项 D:不动点满足 ,不动点为 ,令 ,则 x x 4 x 0 x a 4217 21,排除. an 10 2111131 17 b a a2 , a a2 , a a2 1 选项 A:证明:当 时, ;,213243222242 16 a处理一:可依次迭代到 10 1a a2 a2 1 处理二:当 时, ,则则 n 4 n1 nn22n1 26 64 17 16 17 16 164 6463 1162 ,则 .an1 (n 4) a10 1 1 1 4 7 10 16 16 2故选 A a【点睛】遇到此类问题,不少考生会一筹莫展.利用函数方程思想,通过研究函数的不动点,进一步讨论 的可能取值,利用“排除法”求解. 非选择题部分(共 110分) 二、填空题:本大题共 7小题,多空题每题 6分,单空题每题 4分,共 36分 1i( 为虚数单位),则 | z | ________. z 11.复数 1 i 2【答案】 2【解析】 【分析】 z..本题先计算 ,而后求其模或直接利用模的性质计算 容易题,注重基础知识、运算求解能力的考查. 112【详解】| z | .|1 i | 22【点睛】本题考查了复数模的运算,属于简单题. Cr,半径长是 .若直线 (0,m) 2x y 3 0 A(2,1) 12.已知圆 m 的圆心坐标是 与圆相切于点 ,则 r _____, ______. 【答案】 (1). (2). m2 r 5 【解析】 【分析】 (0,m) 本题主要考查圆的方程、直线与圆的位置关系.首先通过确定直线 的斜率,进一步得到其方程,将 AC m代入后求得 ,计算得解. 11(0,m) kAC AC : y 1 (x 2) 【 详 解 】 可 知 , 把 代 入 得 , 此 时 m 2 22.r | AC | 4 1 5 【点睛】:解答直线与圆的位置关系问题,往往要借助于数与形的结合,特别是要注意应用圆的几何性质. 13.在二项式 9 的展开式中,常数项是________;系数为有理数的项的个数是_______. ( 2 x) 【答案】 (1). (2). 516 2 【解析】 【分析】 本题主要考查二项式定理、二项展开式的通项公式、二项式系数,属于常规题目.从写出二项展开式的通项 x入手,根据要求,考察 的幂指数,使问题得解. Tr1 C9r ( 2)9r xr (r 0,1,29) 【详解】 9 的通项为 ( 2 x) 09可得常数项为 ,T C9 ( 2) 16 2 1r =1,3,5,7,9 T ,T ,T ,T ,T 10 共 5 个项 2 4 6 8 因系数为有理数, ,有 【点睛】此类问题解法比较明确,首要的是要准确记忆通项公式,特别是“幂指数”不能记混,其次,计 算要细心,确保结果正确. VABC A C 上,若 14. 中, ,,,点 在线段 D,则 ABC 90 BC 3 BDC 45 在AB 4 ____; cosABD ________. BD 12 2 57 2 【答案】 (1). (2). 10 【解析】 【分析】 本题主要考查解三角形问题,即正弦定理、三角恒等变换、数形结合思想及函数方程思想.通过引入 BDC .CD x ,在 、中应用正弦定理,建立方程,进而得解. ABD AB BD 3 4AB 4,ADB 【详解】在 中,正弦定理有: ,而 ,ABD sin ADB sin BAC BC AC 3AB 4512 2 522sin BAC ,cosBAC ,,所以 .BD AC AB BC 5 5AC 447 2 10 cosABD cos(BDC BAC) cos cosBAC sin sinBAC 【点睛】解答解三角形问题,要注意充分利用图形特征. x2 y2 x的左焦点为 ,点 在椭圆上且在轴的上方,若线段 15.已知椭圆 的中点在以原点 为PO1 FPF 95O F 圆心, 为半径的圆上,则直线 的斜率是_______. PF 【答案】 15 【解析】 【分析】 结合图形可以发现,利用三角形中位线定理,将线段长度用坐标表示考点圆的方程,与椭圆方程联立可进 一步求解.利用焦半径及三角形中位线定理,则更为简洁. |OF|=|OM |= c= 2 【详解】方法 1:由题意可知 ,可得 (x 2)2 y2 16 ,PF 2 | OM | 4 P(x, y) 由中位线定理可得 ,设 1×2 y2 联立方程 1 95321 2x在椭圆上且在 轴的上方, x , x 可解得 (舍),点 P215 315 221P , 求得 ,所以 kPF 15 22方法 2:焦半径公式应用 |OF |=|OM |= c= 2 解析 1:由题意可知 ,32PF 2 | OM | 4 a ex 4 x 由中位线定理可得 ,即 1pp15 315 221P , 求得 ,所以 .kPF 15 22【点睛】本题主要考查椭圆的标准方程、椭圆的几何性质、直线与圆的位置关系,利用数形结合思想,是 解答解析几何问题的重要途径. 23a,则实数 的最大值是 | f (t 2) f (t) | 16.已知 ____. ,函数 ,若存在 ,使得 a R f (x) ax x t R 34a【答案】 max 3【解析】 【分析】 本 题 主 要 考 查 含 参 绝 对 值 不 等 式 、 函 数 方 程 思 想 及 数 形 结 合 思 想 , 属 于 能 力 型 考 题 . 从 研 究 f (t 2) f (t) 2a 3t2 6t 4 2 入手,令 m 3t2 6t 4[1,),从而使问题加以转化,通过绘制 函数图象,观察得解. f (t 2) f (t) a 2(t 2)2 t(t 2) t2 ) 2 2a 3t2 6t 4 2 【详解】使得 ,13使得令 m 3t2 6t 4[1,),则原不等式转化为存在 ,由折线函数,如图 m 1, |am 1| 134343a,即 的最大值是 a 1 a 只需 ,即 【点睛】对于函数不等式问题,需充分利用转化与化归思想、数形结合思想. (i 1,2,3,4,5,6) 17.已知正方形 的边长为 1,当每个 取遍 时, ABCD i 的最小值是________;最大值是_______. | 1 AB 2 BC 3CD 4 DA 5 AC 6 BD | 【答案】 (1). 0 (2). 2 5 【解析】 【分析】 本题主要考查平面向量的应用,题目难度较大.从引入“基向量”入手,简化模的表现形式,利用转化与化 归思想将问题逐步简化. 【详解】 AB BC CD DA AC BD AB AD 6 6 123456135245 AB BC CD DA AC BD 要使 的最小,只需要 123456 0 1, 1, 1, 1, 1, 1 ,此时只需要取 13562456123456 6 AB BC CD DA AC BD 0 此时 12345min , , , , 等号成立当且仅当 6 均非负或者均非正,并且 6 均非负或者均非正。 135245 1, 1, 1, 1, 1, 1 比如 123456 6 AB BC CD DA AC BD 20 2 5 .则12345max 点睛:对于此题需充分利用转化与化归思想,从“基向量”入手,最后求不等式最值,是一道向量和不等 式的综合题。 【点睛】对于平面向量的应用问题,需充分利用转化与化归思想、数形结合思想. 三、解答题:本大题共 5小题,共 74分,解答应写出文字说明、证明过程或演算步骤. f (x) sinx, xR 18.设函数 . [0,2), f (x ) (1)已知 (2)求函数 函数 是偶函数,求 的值; 12 y [ f (x )]2 [ f (x )]2 的值域. 433 3 , 1 ,1 【答案】(1) ;(2) .222 2 【解析】 【分析】 (1)由函数的解析式结合偶函数的性质即可确定 的值; y asin x b (2)首先整理函数的解析式为 的形式,然后确定其值域即可. f x sin x 【详解】(1)由题意结合函数的解析式可得: ,22 0,2 k 0,1 x k k Z k k Z 函数为偶函数,则当 时, ,即 ,结合 可取 ,x 0 3 2 2 , 相应的 值为 .12 4y sin2 x sin2 x (2)由函数的解析式可得: 62221 cos 2x 1 cos 2x 1 26 1 cos 2x cos 2x 212311 1 1 cos2x sin 2x sin 2x 221233cos2x sin 2x 2236.sin 2x 2331 ,1 的据此可得函数 值域为: .22【点睛】本题主要考查由三角函数的奇偶性确定参数值,三角函数值域的求解,三角函数式的整理变形等 知识,意在考查学生的转化能力和计算求解能力. ABC A B C 1 ,平面 A AC C 19.如图,已知三棱柱 平面 ,,ABC ABC 90 1111BAC 30, A A AC AC, E, F AC, A B 1 的中点. 1分别是 11(1)证明: (2)求直线 ;EF BC A BC 与平面 所成角的余弦值. EF 13【答案】(1)证明见解析;(2) . 5【解析】 【分析】 (1)由题意首先证得线面垂直,然后利用线面垂直的定义即可证得线线垂直; (2)建立空间直角坐标系,分别求得直线的方向向量和平面的法向量,然后结合线面角的正弦值和同角三角 函数基本关系可得线面角的余弦值. A E, B E 【详解】(1)如图所示,连结 ,113△AAC AE EC 等边 中, ,则 ,sin B 0,sin A 12A AC C A ACC AC 平面 ABC⊥平面 1 ,且平面 ABC∩平面 A E ,,111A E⊥BC 由面面垂直的性质定理可得: 平面 ,故 ABC 11A B∥AB A B BC A B A E A 由三棱柱的性质可知 ,而 ,故 ,且 ,AB BC 11111111A B E 由线面垂直的判定定理可得: 平面 ,BC 11A B E 结合 ⊆平面 ,故 .EF BC EF 11EA (2)在底面 ABC 内作 EH⊥AC,以点 E 为坐标原点,EH,EC, 1 方向分别为 x,y,z 轴正方向建立空间直角坐标 E xyz 系.设EH 1,则 ,AA CA 2 3 ,,BC 3, AB 3 AE EC 3 1133A 0, 3,0 ,B ,,0 ,A 0,0,3 ,C 0, 3,0 据此可得: 1 ,2 2 3 3 ,BB3,3 由1 可得点 1 的坐标为 ,AB A B 112 2 3 3 ,E 0,0,0 F3,3 利用中点坐标公式可得: ,由于 ,4 4 3 3 ,EF 3,3 故直线 EF 的方向向量为: 4 4 A BC m x, y, z 设平面 的法向量为 ,则: 1 3333m A B x, y, z ,,3 x y 3z 0 12 2 22, 3333 m BC x, y, z , ,0 x y 0 2 2 22 EF 3 3 ,A BC m 1, 3,1 3,3 据此可得平面 的一个法向量为 ,14 4 cos EF,m EF m 645 此时 ,3 5 2EF m 5 sin cos EF,m ,cos 435A BC 设直线 EF 与平面 所成角为 ,则 .15【点睛】本题考查了立体几何中的线线垂直的判定和线面角的求解问题,意在考查学生的空间想象能力和 逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严 密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向 量的夹角公式求解. n的前 项和为 {a } Sa 4 a S ,b,数列 满足:对每 n20.设等差数列 , nn343nN, Sn bn , Sn1 bn , Sn2 b n 成等比数列. {a },{b } (1)求数列 的通项公式; nnan ,nN, C (2)记 证明: C1 C2 + Cn 2 n,nN . n2bn a 2 n 1 b n n1 ;(2)证明见解析. 【答案】(1) ,nn【解析】 【分析】 aa n(1)首先求得数列 的首项和公差确定数列 的通项公式,然后结合三项成等比数列的充分必要条件整 nb理计算即可确定数列 的通项公式; nc n(2)结合(1)的结果对数列 的不等式. 的通项公式进行放缩,然后利用不等式的性质和裂项求和的方法即可证得题中 a1 2d 4 a 0 1【详解】(1)由题意可得: ,解得: ,32 d 2 a1 3d 3a1 d2a则数列 的通项公式为. n0 2n 2 n 其前 n 项和 .Sn n n1 2n n1 b ,n n1 b , n 1 n 2 b 则n 成等比数列,即: nn2,n n1 b n n1 b n 1 n 2 b nnn 据此有: 2n2 n 1 2n n1 b b2 n n1 n 1 n 2 n 1 n 2 b n n1 b b2 ,n nnnnn2 (n 1)2 n(n 1)(n 1)(n 2) n 1 n 2 n n1 2n n1 b n n1 故.n (2)结合(1)中的通项公式可得: an n 1 n n1 122Cn 2 n n 1 ,2bn nn n n n 1 C C C 2 1 0 2 2 1 2 n n 1 2 n 则.12n【点睛】本题主要考查数列通项公式的求解,,裂项求和的方法,数列中用放缩法证明不等式的方法等知识, 意在考查学生的转化能力和计算求解能力. 2F(1,0) A,B ,点 为焦点,过点 的直线交抛物线于 两点,点 21.如图,已知点 为抛物线 的重心 y 2px( p 0) CFFx在 x 轴上,直线 AC Q Q 轴于点 ,且 在点 右侧.记 在抛物线上,使得 交VABC GFS , S △AFG,△CQG 的面积为 .21p(1)求 的值及抛物线的标准方程; S1 (2)求 的最小值及此时点 的坐标. GS2 3G 2,0 .【答案】(1)1, ;(2) ,x 1 1 2【解析】 【分析】 (1)由焦点坐标确定 p 的值和准线方程即可; (2)设出直线方程,联立直线方程和抛物线方程,结合韦达定理求得面积的表达式,最后结合均值不等式的 S1 结论即可求得 的最小值和点 G 的坐标. S2 py2 4x p 2,2p 4 1 【详解】(1)由题意可得 ,则 ,抛物线方程为 ,准线方程为 .x 1 2A x, y , B x, y (2)设 ,1 2 12设直线 AB 的方程为 ,与抛物线方程 y2 4x 联立可得: y k x1 ,k 0 42 2 22x x 2 , x x1 ,故: ,k x 2k 4 xk 0 222 2 k2 4y y k x x 2 , y y 4x 4×2 4 ,1 12121 2 kC x, y 设点 C 的坐标为 3 ,由重心坐标公式可得: 3141 4 x1 x2 x3 y1 y2 y3 2 x y xG y ,,3 3 G3k2 3 k 33y32 4k2 14418k2 4y 0 x 2 2 y 令可得: ,则 .即 ,x3 GG33k2 k2 3k4y1 y3 y1 y3 4kAC x1 x3 y12 y32 y1 y3 由斜率公式可得: ,444y y x x 直线 AC 的方程为: ,33y1 y3 y y y y y y 3 3 y32 3 3 y1 y3 11y 0 令故且可得: ,,xQ x3 444411 1 8k2 y83k2 13S x x y 2 1 y1 1 F 1G122321y3 y1 y3 138 S x x y 2 3 ,G 2Q224k2 2 y 2841S y 由于 ,代入上式可得: ,23k k3 3k2 k444y1 4y k ,则 y y , y y 4 由则可得 ,1y12 4 121 2 y1 kky81381 42y12 y2 2 2 S1 S2 123k2 48 y12 8 y2 8 16 y2 4 y2 4 2 y 211 11 k k3 3k2 43 2 1 2.48 y12 8 2y2 8 16 148 y12 8 y2 8 2当且仅当 ,即 ,时等号成立 y1 8 4 3y1 6 2 1.4y1 y12 4 18k2 k 2 ,x 2 2 G 2,0 .此时 ,则点 G 的坐标为 G3【点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系, 本题主要考查了抛物线准线方程的求解,直线与抛物线的位置关系,三角形重心公式的应用,基本不等式 求最值的方法等知识,意在考查学生的转化能力和计算求解能力. 22.已知实数 a 0 ,设函数 f (x)=aln x x 1, x 0. 34f (x) a (1)当 时,求函数 的单调区间; 1xa求 的取值范围. x[ ,) (2)对任意 均有 f (x) ,e2 2a 注: 为自然对数的底数. e 2.71828… 2f x 3, 0,3 ,单调递减区间是 ;(2) 【答案】(1) 的单调递增区间是 .0 a 4【解析】 【分析】 (1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可. (2)由题意首先由函数在特殊点的函数值得到 a 的取值范围,然后证明所得的范围满足题意即可. 3430, a f x ln x x 1 【详解】(1)当 时, ,函数的定义域为 ,且: 4x 3 4x 3 313 x 1 2x 4x x1 f ‘ x ,4x 2 x 1 4x x1 3x 1 2x f x 3, 0,3 因此函数 的单调递增区间是 ,单调递减区间是 .x(2)构造函数 ,g x aln x 1 x 2a 1e2 11注意到: g 2a 1 „ 0 ,2ae e2 111111注意到 时恒成立,满足 g 2a 1 „ 0 e2 ;a 0 2a 2 1 1 e2 2ae 2ae ee2 111e2 a 0 当时, g 2a 0 ,不合题意, e2 2ae 122g 1 2 0 且,解得: ,故 .a 0 a 2a 442下面证明 刚好是满足题意的实数 a 的取值范围. 0 a 4分类讨论: x2(a)当 时, ,x 1 g x aln x 1 x ln x 1 x 2x 2a 42令,则: x ln x 1 x 2x 4111 ‘ x 2 2x 2 1 x 2x 1 x 2x 2 x(1 x) 2 2x 1 x 2 2x 1 x 2×2 3x 1 2 2x 1 x( 1 x 2x 2 x(1 x)) 1 x 4×3 8×2 5x 1 ,2 2x 1 x 1 x 2x 2 x(1 x) 22x 1 x 2×2 3x 1 ‘ x 0 x g x x 1 0 易知 ,则函数 单调递减, a ln x x1a a ,满足题意. 11e2 2g x 0 x 1 (b)当 时, 等价于 ,x 0 2左侧是关于 a 的开口向下的二次函数 ,1 x 1 x 2 x ln x x 4ln x x 其判别式 ,x11t2 4t 1 t 4lnt t ‘ 0 令,注意到当 时, ,t x tt2 e115 x 于是 x ,1 2ln 2 0 在上单调递增,而 , 2e4 41 1 x ,2于是当 时命题成立, e 4 1x 1 2ln x xx ,1 a 而当 时,此时 的对称轴为 随着 递增, a 458552于是对称轴在 的右侧,而 成立,(不等式等价于 ). ln 2 a 8ln 2 8ln2 42 a u 因此 1 0 .42综上可得:实数 a 的取值范围是 .0 a 4【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数 的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2) 利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决 生活中的优化问题. (4)考查数形结合思想的应用.
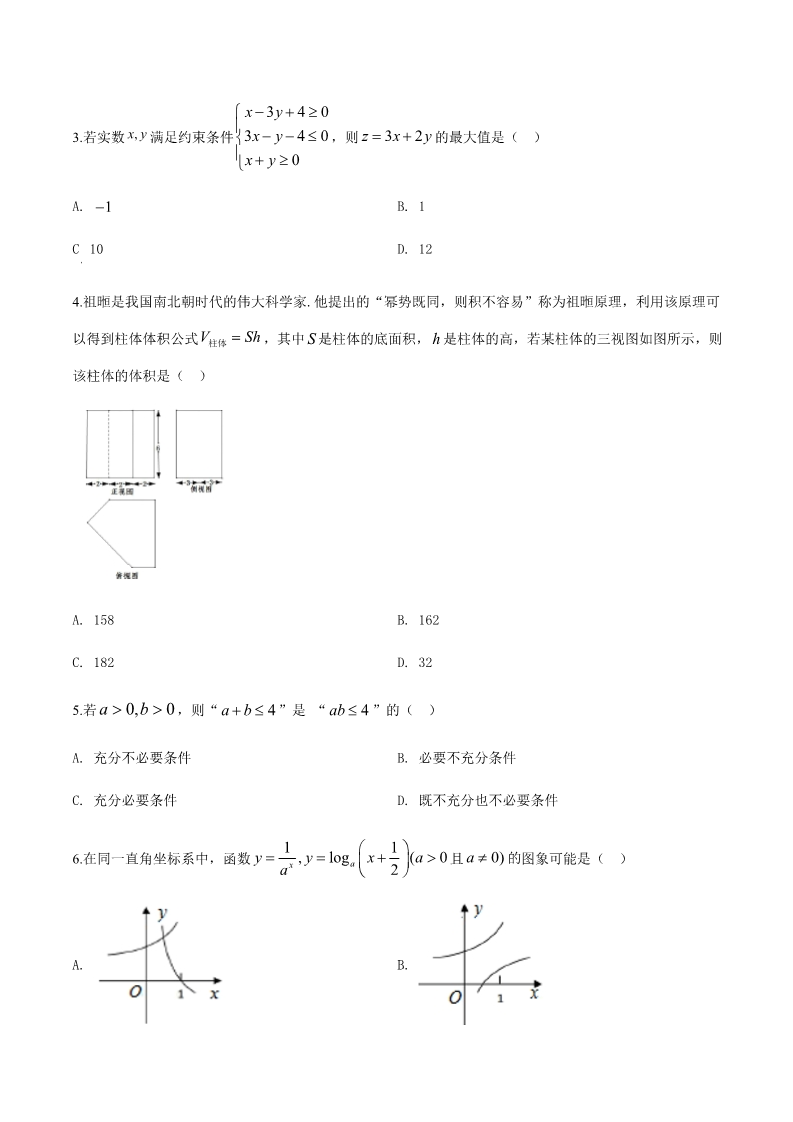
2019年普通高等学校招生全国统一考试(浙江卷)数学 参考公式: P(A B) P(A) P(B) P(AB) P(A)P(B) A, B A, B 若事件 若事件 若事件 互斥,则 柱体的体积公式 V Sh 相互独立,则 其中 表示柱体的底面积, 表示柱体的高 hSp在一次试验中发生的概率是 ,则 nA次1V Sh 3锥体的体积公式 独立重复试验中事件 恰好发生次的概率 kA其中 表示锥体的底面积, Sh表示锥体的高 P (k) Cnk pk (1 p)nk (k 0,1,2,,n) n2球的表面积公式 S 4 R 台体的体积公式 4V R3 球的体积公式 3S , S 其中 分别表示台体的上、下底面积, 表 h12其中 表示球的半径 R示台体的高 选择题部分(共 40分) 一、选择题:本大题共 10小题,每小题 4分,共 40分,在每小题给出的四个选项中,只有一 项是符合题目要求的. U 1,0,1,2,3 A 0,1,2 B 1,0,1 1.已知全集 ,集合 ,,则(∁UA)∩B=( ) 1 0,1 A. C. B. D. 1,2,3 1,0,1,3 x y 0 2.渐近线方程为 的双曲线的离心率是( )2A. B. 1 D. 2 2C. 2x 3y 4 0 3x y 4 0 x y 0 x, y z 3x 2y 3.若实数 满足约束条件 ,则 的最大值是( )A. B. 1 1 C 10 .D. 12 4.祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容易”称为祖暅原理,利用该原理可 V Sh 以得到柱体体积公式 该柱体的体积是( ,其中 是柱体的底面积, 是柱体的高,若某柱体的三视图如图所示,则 hS柱体 )A. 158 C. 182 B. 162 D. 32 a 0,b 0 5.若 ,则“ ”是 “ ”的( )a b 4 ab 4 A. 充分不必要条件 C. 充分必要条件 B. 必要不充分条件 D. 既不充分也不必要条件 112y , y log x (a 0 a 0) 的6.在同一直角坐标系中,函数 且图象可能是( )a ax A. B. C. D. 7.设 ,则随机变量 的分布列是: X0 a 1 a0,1 则当 在内增大时( )D X D X 减小 A. C. 增大 B. D. D X D X 先增大后减小 先减小后增大 V ABC 的底面是正三角形,侧棱长均相等, 8.设三棱锥 是棱 上的点(不含端点),记直线 与VA PPB 的平面角为 ,则( 所成角为 ,二面角 所成角为,直线 直线 与平面 PB )AC ABC P AC B , , , A. C. B. D. , x, x 0 a,b R f (x) y f (x) ax b 9.已知 ,函数 ,若函数 恰有三个零点,则 1 1×3 (a 1)x2 ax, x 0 32()a 1,b 0 a 1,b 0 a 1,b 0 A. B. D. C. a 1,b0 a,b R , 则( )2a10.设 ,数列 中,a =a,a =a +b, nN 1n+1 nn,11b ,a 10 b ,a 10 A. 当 C. 当 B. 当 D. 当 10 10 24b 2,a 10 b 4,a 10 10 10 非选择题部分(共 110分) 二、填空题:本大题共 7小题,多空题每题 6分,单空题每题 4分,共 36分 1i( 为虚数单位),则 | z | z 11.复数 ________. 1 i m A(2,1) ,则 _____, 2x y 3 0 与圆相切于点 Cr,半径长是 .若直线 (0,m) 12.已知圆 的圆心坐标是 ______. r 13.在二项式 9 的展开式中,常数项是________;系数为有理数的项的个数是_______. ( 2 x) 14.在 中, ,,,点 在线段 上,若BDC 45,则 VABC ABC 90 BC 3 AC BD ____; AB 4 DcosABD ________. x2 y2 在椭圆上且在 x轴的上方,若线段 15.已知椭圆 的左焦点为 ,点 F的中点在以原点 为圆 OPF 1 P95OF 心, 为半径的圆上,则直线 的斜率是_______. PF 233a,则实数 的最大值是 | f (t 2) f (t) | 16.已知 ,函数 ,若存在 ,使得 a R f (x) ax x t R ____. (i 1,2,3,4,5,6) 17.已知正方形 的边长为 1,当每个 取遍 时, ABCD i 的最小值是________;最大值是_______. | 1 AB 2 BC 3CD 4 DA 5 AC 6 BD | 三、解答题:本大题共 5小题,共 74分,解答应写出文字说明、证明过程或演算步骤. f (x) sinx, xR 18.设函数 . [0,2), f (x ) (1)已知 (2)求函数 函数 是偶函数,求 的值; 12 y [ f (x )]2 [ f (x )]2 的值域. 4ABC A B C 1 ,平面 A AC C 19.如图,已知三棱柱 平面 ,,ABC ABC 90 1111BAC 30, A A AC AC, E, F AC, A B 1 的中点. 1分别是 11(1)证明: (2)求直线 ;EF BC A BC 与平面 所成角的余弦值. EF 1n{a } Sa 4 a S ,b,数列 满足:对每 n的前20.设等差数列 项和为 , nn343nN, Sn bn , Sn1 bn , Sn2 b n 成等比数列. {a },{b } (1)求数列 的通项公式; nnan ,nN, C (2)记 证明: C1 C2 + Cn 2 n,nN . n2bn 2A,B ,点 为焦点,过点 的直线交抛物线于 两点,点 21.如图,已知点 F(1,0)为抛物线 y 2px( p 0) CFFxx轴于点 ,且 在点 右侧.记 QQ在抛物线上,使得 的重心 在轴上,直线 交VABC GFAC S , S △AFG,△CQG 的面积为 .21p(1)求 的值及抛物线的标准方程; S1 (2)求 的最小值及此时点 的坐标. GS2 22.已知实数 a 0 ,设函数 f (x)=aln x x 1, x 0. 3f (x) a (1)当 时,求函数 的单调区间; 41xa求 的取值范围. x[ ,) (2)对任意 均有 f (x) ,e2 2a 注: 为自然对数的底数. e 2.71828… 2019年普通高等学校招生全国统一考试(浙江卷)数学 参考公式: P(A B) P(A) P(B) P(AB) P(A)P(B) A, B A, B 若事件 若事件 若事件 互斥,则 柱体的体积公式 V Sh 相互独立,则 其中 表示柱体的底面积, 表示柱体的高 hSp,则 n 次 A在一次试验中发生的概率是 1V Sh 3锥体的体积公式 独立重复试验中事件 恰好发生次的概率 kA其中 S表示锥体的底面积, 表示锥体的高 hP (k) Cnk pk (1 p)nk (k 0,1,2,,n) n2球的表面积公式 S 4 R 台体的体积公式 4V R3 球的体积公式 3S , S 其中 分别表示台体的上、下底面积, 表 h12其中 表示球的半径 R示台体的高 选择题部分(共 40分) 一、选择题:本大题共 10小题,每小题 4分,共 40分,在每小题给出的四个选项中,只有一 项是符合题目要求的. U 1,0,1,2,3 A 0,1,2 B 1,0,1 1.已知全集 ,集合 ,,则(∁UA)∩B=( ) 1 A. C. B. D. 0 , 1 1,2,3 1,0,1,3 【答案】A 【解析】 【分析】 本题借根据交集、补集的定义可得.容易题,注重了基础知识、基本计算能力的考查. C A={1,3} C A B {1} 【详解】 ,则 UU【点睛】易于理解集补集的概念、交集概念有误. x y 0 2.渐近线方程为 的双曲线的离心率是( )2A. B. 1 D. 2 2C. 2【答案】C 【解析】 【分析】 .,进一步可得离心率 容易题,注重了双曲线基础知识、基本 本题根据双曲线的渐近线方程可求得 a b 1 计算能力的考查. 22x y 0 【详解】因为双曲线的渐近线为 ,所以 a=b=1,则 ,双曲线的离心率 c a b 2 ce 2 .a【点睛】理解概念,准确计算,是解答此类问题的基本要求.部分考生易出现理解性错误. x 3y 4 0 3x y 4 0 x y 0 x,y 3.若实数 满足约束条件 z 3x 2y ,则 的最大值是( )A. B. 1 1 C. 10 D. 12 【答案】C 【解析】 【分析】 本题是简单线性规划问题的基本题型,根据“画、移、解”等步骤可得解.题目难度不大题,注重了基础知 识、基本技能的考查. (-1,1),(1,-1),(2,2) 【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以 为顶点的三角形 z=3x+2y (2,2) z=3x+2y 时, 取最大值 区域(包含边界),由图易得当目标函数 经过平面区域的点 zmax 32 22 10 .【点睛】解答此类问题,要求作图要准确,观察要仔细.往往由于由于作图欠准确而影响答案的准确程度, 也有可能在解方程组的过程中出错. 4.祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容易”称为祖暅原理,利用该原理可 V Sh 以得到柱体体积公式 ,其中 是柱体的底面积,是柱体的高,若某柱体的三视图如图所示,则该 S柱体 柱体的体积是( )A. 158 B. 162 D. 32 C. 182 【答案】B 【解析】 【分析】 本题首先根据三视图,还原得到几何体—棱柱,根据题目给定的数据,计算几何体的体积.常规题目.难度不 大,注重了基础知识、视图用图能力、基本计算能力的考查. 【详解】由三视图得该棱柱的高为 6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为 4,下 底 为6 , 高 为3 , 另 一 个 的 上 底 为2 , 下 底 为6 , 高 为3 , 则 该 棱 柱 的 体 积 为 2 6 24 6 23 3 6 162 .【点睛】易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心算. a 0,b 0 5.若 ,则“ ”是 “ ”的( )a b 4 ab 4 A. 充分不必要条件 C. 充分必要条件 【答案】A B. 必要不充分条件 D. 既不充分也不必要条件 【解析】 【分析】 a,b 的本题根据基本不等式,结合选项,判断得出充分性成立,利用“特殊值法”,通过特取 值,推出矛盾, .确定必要性不成立 题目有一定难度,注重重要知识、基础知识、逻辑推理能力的考查. a > 0, b > 0 【详解】当 性成立;当 时, ,则当 时,有 ,解得 ,充分 a b 4 ab 4 a b 2 ab 2 ab a b 4 a=1, b=4 时,满足 ,但此时 a+b=5>4 ,必要性不成立,综上所述,“ ”是 ab 4 a b 4 “”的充分不必要条件. ab 4 【点睛】易出现的错误有,一是基本不等式掌握不熟,导致判断失误;二是不能灵活的应用“赋值法”,通 a,b 过特取 的值,从假设情况下推出合理结果或矛盾结果. 112y , y log x (a 0 a 0) 6.在同一直角坐标系中,函数 且的图象可能是( )a ax A. B. C. D. 【答案】D 【解析】 【分析】 a本题通过讨论 的不同取值情况,分别讨论本题指数函数、对数函数的图象和,结合选项,判断得出正确结 论.题目不难,注重重要知识、基础知识、逻辑推理能力的考查. 1ax 时,函数 y ax 过定点 且单调递减,则函数 过定点 (0,1) (0,1) 且单调递增,函 y 【详解】当 0 a 1 11y ax y log x (0,1) 且单调递 ( ,0) 数过定点 且单调递减,D 选项符合;当 时,函数 过定点 a 1 a 2211ax 12(0,1) y log x y ( ,0) 增,则函数 过定点 且单调递减,函数 过定点 且单调递增,各选项均不 a 2符合.综上,选 D. 【点睛】易出现的错误有,一是指数函数、对数函数的图象和性质掌握不熟,导致判断失误;二是不能通 a过讨论 的不同取值范围,认识函数的单调性. 7.设 ,则随机变量 的分布列是: X0 a 1 a0,1 则当 在内增大时( )D X D X 减小 A. C. 增大 B. D. D X D X 先增大后减小 先减小后增大 【答案】D 【解析】 【分析】 aa研究方差随 变化的增大或减小规律,常用方法就是将方差用参数 表示,应用函数知识求解本题根据方 .a差与期望的关系,将方差表示为 的二次函数,二测函数的图象和性质解题题目有一定综合性,注重重要 .知识、基础知识、运算求解能力的考查. 1 a 3E(X ) 【详解】方法 1:由分布列得 ,则 22 0 2 a 2 1 1 a 311 a 311 a 31291216a(0,1) 内增大时, ,则当 在D(X ) a 333D(X ) 先减小后增大. 2a2 1 (a 1)2 2a2 2a 2 D(X ) E X2 E(X ) 0 2913a 方法 2:则 故选 D. 339924【点睛】易出现的错误有,一是数学期望、方差以及二者之间的关系掌握不熟,无从着手;二是计算能力 差,不能正确得到二次函数表达式. V ABC 8.设三棱锥 的底面是正三角形,侧棱长均相等, 是棱VA 上的点(不含端点),记直线 与直 PPB 的平面角为 ,则( 所成角为 ,二面角 所成角为,直线 线与平面 PB )AC ABC P AC B , , , A. B. D. , C. 【答案】B 【解析】 【分析】 本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的 计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则 可事倍功半. AC VABC O的投影为 ,则 AO P在底面投影 在线段 上,过 【详解】方法 1:如图 为中点, 在底面 GDD作DE 垂直 ,易得 PE / /VG ,过 P作交PF // AC VG 于,过 作,交 于,则 DH / /AC BG AE FDHPF EG DH BD BPF, PBD, PED cos cos , 则 , 即 ,PB PB PB PB PD PD y tan tan ,即 ,综上所述,答案为 B. ED BD 的平面角为 (显然 方法 2:由最小角定理 ,记 )V AB C 由最大角定理 ,故选 B. V ABC 法 2:(特殊位置)取 为正四面体, 为中点,易得 VA P333 622 2 ,故选 B. cos sin ,sin , sin 633【点睛】常规解法下易出现的错误有,不能正确作图得出各种角.未能想到利用“特殊位置法”,寻求简便解 法. x, x 0 a,b R f (x) y f (x) ax b 9.已知 ,函数 ,若函数 恰有三个零点,则 1 1×3 (a 1)x2 ax, x 0 32()a 1,b 0 a1,b0 A. B. D. a 1,b 0 C. a 1,b0 【答案】D 【解析】 【分析】 本题综合性较强,注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函 数方程的方法较为灵活,通常需要结合函数的图象加以分析. y f (x) y ax b ,有三个交点. 【详解】原题可转化为 与f (0) 0, f (0) a 当时, f (x) x2 (a 1)x a (x a)(x 1) ,且 ,则 BC AP y f (x) y ax b 不可能有三个交点(实际上有一个),排除 A,B (1)当 时,如图 与a 1 y f (x) y ax b (2)当 时,分三种情况,如图 a1 与若有三个交点,则 ,答案选 D b 0 下面证明: a 1时, 时11F(x) f (x) ax b x3 (a 1)x2 b ,F (x) x2 (a 1)x x(x (a 1)) ,则 BC AP 3210 b (a 1)3 F(0) > 0 ,F(a+1)<0 ,才能保证至少有两个零点,即 ,若另一零点在 0 6a,b 【点睛】遇到此类问题,不少考生会一筹莫展.由于方程中涉及 两个参数,故按“一元化”想法,逐步 .分类讨论,这一过程中有可能分类不全面、不彻底 . , ,则( )2aa,b R ,数列 10.设 中,a1=a,an+1=a +b, nnN n11b ,a 10 b ,a 10 A. 当 B. 当 10 10 24b 2,a 10 b 4,a 10 C. 当 D. 当 10 10 【答案】A 【解析】 【分析】 本题综合性较强,注重重要知识、基础知识、运算求解能力、分类讨论思想的考查.本题从确定不动点出发, 通过研究选项得解. 21121122a a 0, ,an 【详解】选项 B:不动点满足 时,如图,若 ,x x x 0 124排除 1212a如图,若 为不动点 a 则n2ax 1 1292a 2 10 选项 C:不动点满足 排除 ,不动点为 ,令 ,则 ,a 2 x x 2 x 0 n2421217 17 1217 2122选项 D:不动点满足 ,不动点为 ,令 ,则 x x 4 x 0 x a 4217 21,排除. an 10 2111131 17 b a a2 , a a2 , a a2 1 选项 A:证明:当 时, ;,213243222242 16 a处理一:可依次迭代到 10 1a a2 a2 1 处理二:当 时, ,则则 n 4 n1 nn22n1 26 64 17 16 17 16 164 6463 1162 ,则 .an1 (n 4) a10 1 1 1 4 7 10 16 16 2故选 A a【点睛】遇到此类问题,不少考生会一筹莫展.利用函数方程思想,通过研究函数的不动点,进一步讨论 的可能取值,利用“排除法”求解. 非选择题部分(共 110分) 二、填空题:本大题共 7小题,多空题每题 6分,单空题每题 4分,共 36分 1i( 为虚数单位),则 | z | ________. z 11.复数 1 i 2【答案】 2【解析】 【分析】 z..本题先计算 ,而后求其模或直接利用模的性质计算 容易题,注重基础知识、运算求解能力的考查. 112【详解】| z | .|1 i | 22【点睛】本题考查了复数模的运算,属于简单题. Cr,半径长是 .若直线 (0,m) 2x y 3 0 A(2,1) 12.已知圆 m 的圆心坐标是 与圆相切于点 ,则 r _____, ______. 【答案】 (1). (2). m2 r 5 【解析】 【分析】 (0,m) 本题主要考查圆的方程、直线与圆的位置关系.首先通过确定直线 的斜率,进一步得到其方程,将 AC m代入后求得 ,计算得解. 11(0,m) kAC AC : y 1 (x 2) 【 详 解 】 可 知 , 把 代 入 得 , 此 时 m 2 22.r | AC | 4 1 5 【点睛】:解答直线与圆的位置关系问题,往往要借助于数与形的结合,特别是要注意应用圆的几何性质. 13.在二项式 9 的展开式中,常数项是________;系数为有理数的项的个数是_______. ( 2 x) 【答案】 (1). (2). 516 2 【解析】 【分析】 本题主要考查二项式定理、二项展开式的通项公式、二项式系数,属于常规题目.从写出二项展开式的通项 x入手,根据要求,考察 的幂指数,使问题得解. Tr1 C9r ( 2)9r xr (r 0,1,29) 【详解】 9 的通项为 ( 2 x) 09可得常数项为 ,T C9 ( 2) 16 2 1r =1,3,5,7,9 T ,T ,T ,T ,T 10 共 5 个项 2 4 6 8 因系数为有理数, ,有 【点睛】此类问题解法比较明确,首要的是要准确记忆通项公式,特别是“幂指数”不能记混,其次,计 算要细心,确保结果正确. VABC A C 上,若 14. 中, ,,,点 在线段 D,则 ABC 90 BC 3 BDC 45 在AB 4 ____; cosABD ________. BD 12 2 57 2 【答案】 (1). (2). 10 【解析】 【分析】 本题主要考查解三角形问题,即正弦定理、三角恒等变换、数形结合思想及函数方程思想.通过引入 BDC .CD x ,在 、中应用正弦定理,建立方程,进而得解. ABD AB BD 3 4AB 4,ADB 【详解】在 中,正弦定理有: ,而 ,ABD sin ADB sin BAC BC AC 3AB 4512 2 522sin BAC ,cosBAC ,,所以 .BD AC AB BC 5 5AC 447 2 10 cosABD cos(BDC BAC) cos cosBAC sin sinBAC 【点睛】解答解三角形问题,要注意充分利用图形特征. x2 y2 x的左焦点为 ,点 在椭圆上且在轴的上方,若线段 15.已知椭圆 的中点在以原点 为PO1 FPF 95O F 圆心, 为半径的圆上,则直线 的斜率是_______. PF 【答案】 15 【解析】 【分析】 结合图形可以发现,利用三角形中位线定理,将线段长度用坐标表示考点圆的方程,与椭圆方程联立可进 一步求解.利用焦半径及三角形中位线定理,则更为简洁. |OF|=|OM |= c= 2 【详解】方法 1:由题意可知 ,可得 (x 2)2 y2 16 ,PF 2 | OM | 4 P(x, y) 由中位线定理可得 ,设 1×2 y2 联立方程 1 95321 2x在椭圆上且在 轴的上方, x , x 可解得 (舍),点 P215 315 221P , 求得 ,所以 kPF 15 22方法 2:焦半径公式应用 |OF |=|OM |= c= 2 解析 1:由题意可知 ,32PF 2 | OM | 4 a ex 4 x 由中位线定理可得 ,即 1pp15 315 221P , 求得 ,所以 .kPF 15 22【点睛】本题主要考查椭圆的标准方程、椭圆的几何性质、直线与圆的位置关系,利用数形结合思想,是 解答解析几何问题的重要途径. 23a,则实数 的最大值是 | f (t 2) f (t) | 16.已知 ____. ,函数 ,若存在 ,使得 a R f (x) ax x t R 34a【答案】 max 3【解析】 【分析】 本 题 主 要 考 查 含 参 绝 对 值 不 等 式 、 函 数 方 程 思 想 及 数 形 结 合 思 想 , 属 于 能 力 型 考 题 . 从 研 究 f (t 2) f (t) 2a 3t2 6t 4 2 入手,令 m 3t2 6t 4[1,),从而使问题加以转化,通过绘制 函数图象,观察得解. f (t 2) f (t) a 2(t 2)2 t(t 2) t2 ) 2 2a 3t2 6t 4 2 【详解】使得 ,13使得令 m 3t2 6t 4[1,),则原不等式转化为存在 ,由折线函数,如图 m 1, |am 1| 134343a,即 的最大值是 a 1 a 只需 ,即 【点睛】对于函数不等式问题,需充分利用转化与化归思想、数形结合思想. (i 1,2,3,4,5,6) 17.已知正方形 的边长为 1,当每个 取遍 时, ABCD i 的最小值是________;最大值是_______. | 1 AB 2 BC 3CD 4 DA 5 AC 6 BD | 【答案】 (1). 0 (2). 2 5 【解析】 【分析】 本题主要考查平面向量的应用,题目难度较大.从引入“基向量”入手,简化模的表现形式,利用转化与化 归思想将问题逐步简化. 【详解】 AB BC CD DA AC BD AB AD 6 6 123456135245 AB BC CD DA AC BD 要使 的最小,只需要 123456 0 1, 1, 1, 1, 1, 1 ,此时只需要取 13562456123456 6 AB BC CD DA AC BD 0 此时 12345min , , , , 等号成立当且仅当 6 均非负或者均非正,并且 6 均非负或者均非正。 135245 1, 1, 1, 1, 1, 1 比如 123456 6 AB BC CD DA AC BD 20 2 5 .则12345max 点睛:对于此题需充分利用转化与化归思想,从“基向量”入手,最后求不等式最值,是一道向量和不等 式的综合题。 【点睛】对于平面向量的应用问题,需充分利用转化与化归思想、数形结合思想. 三、解答题:本大题共 5小题,共 74分,解答应写出文字说明、证明过程或演算步骤. f (x) sinx, xR 18.设函数 . [0,2), f (x ) (1)已知 (2)求函数 函数 是偶函数,求 的值; 12 y [ f (x )]2 [ f (x )]2 的值域. 433 3 , 1 ,1 【答案】(1) ;(2) .222 2 【解析】 【分析】 (1)由函数的解析式结合偶函数的性质即可确定 的值; y asin x b (2)首先整理函数的解析式为 的形式,然后确定其值域即可. f x sin x 【详解】(1)由题意结合函数的解析式可得: ,22 0,2 k 0,1 x k k Z k k Z 函数为偶函数,则当 时, ,即 ,结合 可取 ,x 0 3 2 2 , 相应的 值为 .12 4y sin2 x sin2 x (2)由函数的解析式可得: 62221 cos 2x 1 cos 2x 1 26 1 cos 2x cos 2x 212311 1 1 cos2x sin 2x sin 2x 221233cos2x sin 2x 2236.sin 2x 2331 ,1 的据此可得函数 值域为: .22【点睛】本题主要考查由三角函数的奇偶性确定参数值,三角函数值域的求解,三角函数式的整理变形等 知识,意在考查学生的转化能力和计算求解能力. ABC A B C 1 ,平面 A AC C 19.如图,已知三棱柱 平面 ,,ABC ABC 90 1111BAC 30, A A AC AC, E, F AC, A B 1 的中点. 1分别是 11(1)证明: (2)求直线 ;EF BC A BC 与平面 所成角的余弦值. EF 13【答案】(1)证明见解析;(2) . 5【解析】 【分析】 (1)由题意首先证得线面垂直,然后利用线面垂直的定义即可证得线线垂直; (2)建立空间直角坐标系,分别求得直线的方向向量和平面的法向量,然后结合线面角的正弦值和同角三角 函数基本关系可得线面角的余弦值. A E, B E 【详解】(1)如图所示,连结 ,113△AAC AE EC 等边 中, ,则 ,sin B 0,sin A 12A AC C A ACC AC 平面 ABC⊥平面 1 ,且平面 ABC∩平面 A E ,,111A E⊥BC 由面面垂直的性质定理可得: 平面 ,故 ABC 11A B∥AB A B BC A B A E A 由三棱柱的性质可知 ,而 ,故 ,且 ,AB BC 11111111A B E 由线面垂直的判定定理可得: 平面 ,BC 11A B E 结合 ⊆平面 ,故 .EF BC EF 11EA (2)在底面 ABC 内作 EH⊥AC,以点 E 为坐标原点,EH,EC, 1 方向分别为 x,y,z 轴正方向建立空间直角坐标 E xyz 系.设EH 1,则 ,AA CA 2 3 ,,BC 3, AB 3 AE EC 3 1133A 0, 3,0 ,B ,,0 ,A 0,0,3 ,C 0, 3,0 据此可得: 1 ,2 2 3 3 ,BB3,3 由1 可得点 1 的坐标为 ,AB A B 112 2 3 3 ,E 0,0,0 F3,3 利用中点坐标公式可得: ,由于 ,4 4 3 3 ,EF 3,3 故直线 EF 的方向向量为: 4 4 A BC m x, y, z 设平面 的法向量为 ,则: 1 3333m A B x, y, z ,,3 x y 3z 0 12 2 22, 3333 m BC x, y, z , ,0 x y 0 2 2 22 EF 3 3 ,A BC m 1, 3,1 3,3 据此可得平面 的一个法向量为 ,14 4 cos EF,m EF m 645 此时 ,3 5 2EF m 5 sin cos EF,m ,cos 435A BC 设直线 EF 与平面 所成角为 ,则 .15【点睛】本题考查了立体几何中的线线垂直的判定和线面角的求解问题,意在考查学生的空间想象能力和 逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严 密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向 量的夹角公式求解. n的前 项和为 {a } Sa 4 a S ,b,数列 满足:对每 n20.设等差数列 , nn343nN, Sn bn , Sn1 bn , Sn2 b n 成等比数列. {a },{b } (1)求数列 的通项公式; nnan ,nN, C (2)记 证明: C1 C2 + Cn 2 n,nN . n2bn a 2 n 1 b n n1 ;(2)证明见解析. 【答案】(1) ,nn【解析】 【分析】 aa n(1)首先求得数列 的首项和公差确定数列 的通项公式,然后结合三项成等比数列的充分必要条件整 nb理计算即可确定数列 的通项公式; nc n(2)结合(1)的结果对数列 的不等式. 的通项公式进行放缩,然后利用不等式的性质和裂项求和的方法即可证得题中 a1 2d 4 a 0 1【详解】(1)由题意可得: ,解得: ,32 d 2 a1 3d 3a1 d2a则数列 的通项公式为. n0 2n 2 n 其前 n 项和 .Sn n n1 2n n1 b ,n n1 b , n 1 n 2 b 则n 成等比数列,即: nn2,n n1 b n n1 b n 1 n 2 b nnn 据此有: 2n2 n 1 2n n1 b b2 n n1 n 1 n 2 n 1 n 2 b n n1 b b2 ,n nnnnn2 (n 1)2 n(n 1)(n 1)(n 2) n 1 n 2 n n1 2n n1 b n n1 故.n (2)结合(1)中的通项公式可得: an n 1 n n1 122Cn 2 n n 1 ,2bn nn n n n 1 C C C 2 1 0 2 2 1 2 n n 1 2 n 则.12n【点睛】本题主要考查数列通项公式的求解,,裂项求和的方法,数列中用放缩法证明不等式的方法等知识, 意在考查学生的转化能力和计算求解能力. 2F(1,0) A,B ,点 为焦点,过点 的直线交抛物线于 两点,点 21.如图,已知点 为抛物线 的重心 y 2px( p 0) CFFx在 x 轴上,直线 AC Q Q 轴于点 ,且 在点 右侧.记 在抛物线上,使得 交VABC GFS , S △AFG,△CQG 的面积为 .21p(1)求 的值及抛物线的标准方程; S1 (2)求 的最小值及此时点 的坐标. GS2 3G 2,0 .【答案】(1)1, ;(2) ,x 1 1 2【解析】 【分析】 (1)由焦点坐标确定 p 的值和准线方程即可; (2)设出直线方程,联立直线方程和抛物线方程,结合韦达定理求得面积的表达式,最后结合均值不等式的 S1 结论即可求得 的最小值和点 G 的坐标. S2 py2 4x p 2,2p 4 1 【详解】(1)由题意可得 ,则 ,抛物线方程为 ,准线方程为 .x 1 2A x, y , B x, y (2)设 ,1 2 12设直线 AB 的方程为 ,与抛物线方程 y2 4x 联立可得: y k x1 ,k 0 42 2 22x x 2 , x x1 ,故: ,k x 2k 4 xk 0 222 2 k2 4y y k x x 2 , y y 4x 4×2 4 ,1 12121 2 kC x, y 设点 C 的坐标为 3 ,由重心坐标公式可得: 3141 4 x1 x2 x3 y1 y2 y3 2 x y xG y ,,3 3 G3k2 3 k 33y32 4k2 14418k2 4y 0 x 2 2 y 令可得: ,则 .即 ,x3 GG33k2 k2 3k4y1 y3 y1 y3 4kAC x1 x3 y12 y32 y1 y3 由斜率公式可得: ,444y y x x 直线 AC 的方程为: ,33y1 y3 y y y y y y 3 3 y32 3 3 y1 y3 11y 0 令故且可得: ,,xQ x3 444411 1 8k2 y83k2 13S x x y 2 1 y1 1 F 1G122321y3 y1 y3 138 S x x y 2 3 ,G 2Q224k2 2 y 2841S y 由于 ,代入上式可得: ,23k k3 3k2 k444y1 4y k ,则 y y , y y 4 由则可得 ,1y12 4 121 2 y1 kky81381 42y12 y2 2 2 S1 S2 123k2 48 y12 8 y2 8 16 y2 4 y2 4 2 y 211 11 k k3 3k2 43 2 1 2.48 y12 8 2y2 8 16 148 y12 8 y2 8 2当且仅当 ,即 ,时等号成立 y1 8 4 3y1 6 2 1.4y1 y12 4 18k2 k 2 ,x 2 2 G 2,0 .此时 ,则点 G 的坐标为 G3【点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系, 本题主要考查了抛物线准线方程的求解,直线与抛物线的位置关系,三角形重心公式的应用,基本不等式 求最值的方法等知识,意在考查学生的转化能力和计算求解能力. 22.已知实数 a 0 ,设函数 f (x)=aln x x 1, x 0. 34f (x) a (1)当 时,求函数 的单调区间; 1xa求 的取值范围. x[ ,) (2)对任意 均有 f (x) ,e2 2a 注: 为自然对数的底数. e 2.71828… 2f x 3, 0,3 ,单调递减区间是 ;(2) 【答案】(1) 的单调递增区间是 .0 a 4【解析】 【分析】 (1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可. (2)由题意首先由函数在特殊点的函数值得到 a 的取值范围,然后证明所得的范围满足题意即可. 3430, a f x ln x x 1 【详解】(1)当 时, ,函数的定义域为 ,且: 4x 3 4x 3 313 x 1 2x 4x x1 f ‘ x ,4x 2 x 1 4x x1 3x 1 2x f x 3, 0,3 因此函数 的单调递增区间是 ,单调递减区间是 .x(2)构造函数 ,g x aln x 1 x 2a 1e2 11注意到: g 2a 1 „ 0 ,2ae e2 111111注意到 时恒成立,满足 g 2a 1 „ 0 e2 ;a 0 2a 2 1 1 e2 2ae 2ae ee2 111e2 a 0 当时, g 2a 0 ,不合题意, e2 2ae 122g 1 2 0 且,解得: ,故 .a 0 a 2a 442下面证明 刚好是满足题意的实数 a 的取值范围. 0 a 4分类讨论: x2(a)当 时, ,x 1 g x aln x 1 x ln x 1 x 2x 2a 42令,则: x ln x 1 x 2x 4111 ‘ x 2 2x 2 1 x 2x 1 x 2x 2 x(1 x) 2 2x 1 x 2 2x 1 x 2×2 3x 1 2 2x 1 x( 1 x 2x 2 x(1 x)) 1 x 4×3 8×2 5x 1 ,2 2x 1 x 1 x 2x 2 x(1 x) 22x 1 x 2×2 3x 1 ‘ x 0 x g x x 1 0 易知 ,则函数 单调递减, a ln x x1a a ,满足题意. 11e2 2g x 0 x 1 (b)当 时, 等价于 ,x 0 2左侧是关于 a 的开口向下的二次函数 ,1 x 1 x 2 x ln x x 4ln x x 其判别式 ,x11t2 4t 1 t 4lnt t ‘ 0 令,注意到当 时, ,t x tt2 e115 x 于是 x ,1 2ln 2 0 在上单调递增,而 , 2e4 41 1 x ,2于是当 时命题成立, e 4 1x 1 2ln x xx ,1 a 而当 时,此时 的对称轴为 随着 递增, a 458552于是对称轴在 的右侧,而 成立,(不等式等价于 ). ln 2 a 8ln 2 8ln2 42 a u 因此 1 0 .42综上可得:实数 a 的取值范围是 .0 a 4【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数 的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2) 利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决 生活中的优化问题. (4)考查数形结合思想的应用.
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





