
 第 1 页 共 33 页 2015 年北京市高考数学试卷(文科) 一、选择题(每小题 5 分,共 40 分) 1.(5 分)(2015•北京)若集合 A={x|﹣5<x<2},B={x|﹣3<x<3},则 A∩B=( ) {x|﹣3<x<2} A. {x|﹣5<x<2} B. {x|﹣3<x<3} C. {x|﹣5<x<3} D. 2.(5 分)(2015•北京)圆心为(1,1)且过原点的圆的方程是( ) (x﹣1)2+( y﹣1)2=1 (x﹣1)2+( y﹣1)2=2 22 A. B. C. D. B(x+1) +( y+1)2=1 (x+1) +(y+1 )2=2 3.(5 分)(2015•北京)下列函数中为偶函数的是( ) y=2﹣x 22 A. y=x sinx B. y=x cosx C.y=|lnx| D. 4.(5 分)(2015•北京)某校老年、中年和青年教师的人数见下表,采用分层插样的方法 调查教师的身体状况,在抽取的样本中,青年教师有 320 人,则该样本的老年教师人数为( )类别 人数 900 老年教师 中年教师 青年教师 合计 1800 1600 4300 A.90 B.100 C.180 D.300 5.(5 分)(2015•北京)执行如图所示的程序框图,输出的 k 值为( ) 第 1 页(共 33 页) 第 2 页 共 33 页 A.3 B.4 C.5 D.6 6.(5 分)(2015•北京)设 , 是非零向量,“ A.充分而不必要 B.必要而不充分 =| || |”是“ ”的( ) 条件 条件 C.充分必要条件 D.既不充分也不 必要条件 7.(5 分)(2015•北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) A.1 B. C. D.2 8.(5 分)(2015•北京)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油 时的情况 第 2 页(共 33 页) 第 3 页 共 33 页 加油时间 加油量(升) 加油时的累计 里程(千米) 2015 年 5 月 1 12 35000 日2015 年 5 月 15 48 35600 日注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每 100 千米平均耗 油量为 ( ) A.6 升 B.8 升 C.10 升 D.12 升 二、填空题 9.(5 分)(2015•北京)复数 i(1+i)的实部为 . 10.(5 分)(2015•北京)2﹣3,3 ,log25 三个数中最大数的是 . 11.(5 分)(2015•北京)在△ABC 中,a=3,b= ,∠A= ,则∠B= . 12.(5 分)(2015•北京)已知(2,0)是双曲线 x2﹣ =1(b>0)的一个焦点,则 b= . 13.(5 分)(2015•北京)如图,△ABC 及其内部的点组成的集合记为 D,P(x,y)为 D 中任意一点,则 z=2x+3y 的最大值为 . 14.(5 分)(2015•北京)高三年级 267 位学生参加期末考试,某班 37 位学生的语文成绩 ,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生. 第 3 页(共 33 页) 第 4 页 共 33 页 从这次考试成绩看, ①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是 ; ②在语文和数学系两个科目中,丙同学的成绩名次更靠前的科目是 . 三、解答题(共 80 分) 15.(13 分)(2015•北京)已知函数 f(x)=sinx﹣2 sin2 (1)求 f(x)的最小正周期; (2)求 f(x)在区间[0, ]上的最小值. 16.(13 分)(2015•北京)已知等差数列{an}满足 a1+a2=10,a4﹣a3=2 (1)求{an}的通项公式; (2)设等比数列{bn}满足 b2=a3,b3=a7,问:b6 与数列{an}的第几项相等? 17.(13 分)(2015•北京)某超市随机选取 1000 位顾客,记录了他们购买甲、乙、丙、 丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买. 甲√乙×丙√丁√100 217 200 300 85 ×√×√√√√×√×√×√××××√××98 (1)估计顾客同时购买乙和丙的概率; (2)估计顾客在甲、乙、丙、丁中同时购买 3 种商品的概率; (3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大? 18.(14 分)(2015•北京)如图,在三棱锥 V﹣ABC 中,平面 VAB⊥平面 ABC,△VAB 为等边三角形,AC⊥BC 且 AC=BC= ,O,M 分别为 AB,VA 的中点. (1)求证:VB∥平面 MOC; (2)求证:平面 MOC⊥平面 VAB (3)求三棱锥 V﹣ABC 的体积. 第 4 页(共 33 页) 第 5 页 共 33 页 19.(13 分)(2015•北京)设函数 f(x)= ﹣klnx,k>0. (1)求 f(x)的单调区间和极值; (2)证明:若 f(x)存在零点,则 f(x)在区间(1, )上仅有一个零点. 20.(14 分)(2015•北京)已知椭圆 C:x2+3y2=3,过点 D(1,0)且不过点 E(2,1) 的直线与椭圆 C 交于 A,B 两点,直线 AE 与直线 x=3 交于点 M. (1)求椭圆 C 的离心率; (2)若 AB 垂直于 x 轴,求直线 BM 的斜率; (3)试判断直线 BM 与直线 DE 的位置关系,并说明理由. 第 5 页(共 33 页) 第 6 页 共 33 页 2015 年北京市高考数学试卷(文科) 参考答案与试题解析 一、选择题(每小题 5 分,共 40 分) 1.(5 分)(2015•北京)若集合 A={x|﹣5<x<2},B={x|﹣3<x<3},则 A∩B=( ) {x|﹣3<x<2} A. {x|﹣5<x<2} B. {x|﹣3<x<3} C. {x|﹣5<x<3} D. 考点: 交集及其运算. 菁优网版权所有 专题: 分析: 集合. 直接利用集合 的交集的运算 法则求解即可. 解:集合 解答: A={x|﹣5<x< 2},B={x|﹣3< x<3}, 则 A∩B={x|﹣3 <x<2}. 故选:A. 点评: 本题考查集合 的交集的运算 法则,考查计算 能力. 2.(5 分)(2015•北京)圆心为(1,1)且过原点的圆的方程是( ) (x﹣1)2+( A. (x﹣1)2+( D. 22B. C. B(x+1) +( y+1)2=1 (x+1) +(y+1 )2=2 y﹣1)2=1 y﹣1)2=2 考点: 专题: 分析: 圆的标准方程. 菁优网版权所有 计算题;直线与 圆. 利用两点间距 离公式求出半 径,由此能求出 圆的方程. 解答: 解:由题意知圆 半径 r= ,∴圆的方程为( x﹣1)2+(y﹣1 )2=2. 第 6 页(共 33 页) 第 7 页 共 33 页 故选:D. 点评: 本题考查圆的 方程的求法,解 题时要认真审 题,注意圆的方 程的求法,是基 础题. 3.(5 分)(2015•北京)下列函数中为偶函数的是( ) y=2﹣x D. 22 A. y=x sinx B. y=x cosx C.y=|lnx| 考点: 函数奇偶性的 判断.菁优网版权所有 专题: 分析: 函数的性质及 应用. 首先从定义域 上排除选项 C, 然后在其他选 项中判断﹣x 与 x 的函数值 关系,相等的就 是偶函数. 解答: 解:对于 A,( 2﹣x) sin(﹣x) =﹣x2sinx;是 奇函数; 对于 B,(﹣x) 2cos(﹣x) =x2cosx;是偶 函数; 对于 C,定义域 为(0,+∞), 是非奇非偶的 函数; 对于 D,定义域 为 R,但是 2﹣( ﹣x)=2x≠2﹣x ,2x≠﹣2﹣x;是非 奇非偶的函数; 故选 B 点评: 本题考查了函 数奇偶性的判 第 7 页(共 33 页) 第 8 页 共 33 页 断;首先判断定 义域是否关于 原点对称;如果 不对称,函数是 非奇非偶的函 数;如果对称, 再判断 f(﹣x) 与 f(x) 关系, 相等是偶函数, 相反是奇函数. 4.(5 分)(2015•北京)某校老年、中年和青年教师的人数见下表,采用分层插样的方法 调查教师的身体状况,在抽取的样本中,青年教师有 320 人,则该样本的老年教师人数为( )类别 人数 900 老年教师 中年教师 青年教师 合计 1800 1600 4300 A.90 考点: 专题: 分析: B.100 C.180 D.300 分层抽样方法. 菁优网版权所有 计算题;概率与 统计. 由题意,老年和 青年教师的人 数比为 900: 1600=9:16,即 可得出结论. 解:由题意,老 年和青年教师 的人数比为 900 :1600=9:16, 因为青年教师 有 320 人,所以 老年教师有 180 人, 解答: 故选:C. 点评: 本题考查分层 抽样,考查学生 的计算能力,比 较基础. 第 8 页(共 33 页) 第 9 页 共 33 页 5.(5 分)(2015•北京)执行如图所示的程序框图,输出的 k 值为( ) A.3 B.4 C.5 D.6 考点: 专题: 程序框图.菁优网版权所有 图表型;算法和 程序框图. 分析: 模拟执行程序 框图,依次写出 每次循环得到 的 a,k 的值, 当 a= 时满足 条件 a< ,退 出循环,输出 k 的值为 4. 解答: 解:模拟执行程 序框图,可得 k=0,a=3,q= a= ,k=1 不满足条件 a< ,a= ,k=2 第 9 页(共 33 页) 第 10 页 共 33 页 不满足条件 a< ,a= ,k=3 不满足条件 a< ,a= ,k=4 满足条件 a< , 退出循环,输出 k 的值为 4. 故选:B. 点评: 本题主要考查 了循环结构的 程序框图,属于 基础题. 6.(5 分)(2015•北京)设 , 是非零向量,“ A.充分而不必要 B.必要而不充分 =| || |”是“ ”的( ) 条件 条件 C.充分必要条件 D.既不充分也不 必要条件 考点: 必要条件、充分 条件与充要条 件的判断;平面 向量数量积的 运算.菁优网版权所有 专题: 分析: 平面向量及应 用;简易逻辑. 由便可得到 夹角为 0,从而 得到 ∥ ,而 ∥ 并不能得到 夹角为 0,从而 得不到 ,这样根据充分 条件、必要条件 第 10 页(共 33 页) 第 11 页 共 33 页 的概念即可找 出正确选项. 解:(1) 解答: ;∴时,cos =1; ∴;∴ ∥ ; ∴“ ”是“ ∥ ”的充分 条件; (2) ∥ 时, 的夹角为 0 或 π; ∴,或﹣ ;即 ∥ 得不到 ;∴“ ”不是“ ∥ ”的必 要条件; ∴总上可得“ 第 11 页(共 33 页) 第 12 页 共 33 页 ”是“ ∥ ”的充分 不必要条件. 故选 A. 点评: 考查充分条件, 必要条件,及充 分不必要条件 的概念,以及判 断方法与过程, 数量积的计算 公式,向量共线 的定义,向量夹 角的定义. 7.(5 分)(2015•北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) A.1 考点: 专题: 分析: B. C. D.2 由三视图求面 积、体积.菁优网版权所有 空间位置关系 与距离. 几何体是四棱 锥,且四棱锥的 一条侧棱与底 面垂直,结合直 观图求相关几 何量的数据,可 得答案 解答: 解:由三视图知 :几何体是四棱 锥,且四棱锥的 一条侧棱与底 第 12 页(共 33 页) 第 13 页 共 33 页 面垂直, 底面为正方形 如图: 其中 PA⊥平面 ABCD,底面 ABCD 为正方 形∴PA=1,AB=1, AD=1, ∴PB= ,PC= =.PD= 该几何体最长 棱的棱长为: 故选:C. 点评: 本题考查了由 三视图求几何 体的最长棱长 问题,根据三视 图判断几何体 的结构特征是 解答本题的关 键 8.(5 分)(2015•北京)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油 时的情况 加油时间 加油量(升) 加油时的累计 里程(千米) 2015 年 5 月 1 12 35000 日2015 年 5 月 15 48 35600 日注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每 100 千米平均耗 油量为 ( ) A.6 升 B.8 升 C.10 升 D.12 升 第 13 页(共 33 页) 第 14 页 共 33 页 考点: 专题: 分析: 一次函数的性 质与图象.菁优网版权所有 函数的性质及 应用. 由表格信息,得 到该车加了 48 升的汽油,跑了 600 千米,由此 得到该车每 100 千米平均耗油 量. 解答: 解:由表格信息 ,得到该车加了 48 升的汽油,跑 了 600 千米,所 以该车每 100 千米平均耗油 量 48÷6=8; 故选:B. 点评: 本题考查了学 生对表格的理 解以及对数据 信息的处理能 力. 二、填空题 9.(5 分)(2015•北京)复数 i(1+i)的实部为 ﹣1 . 考点: 专题: 分析: 复数的基本概 念.菁优网版权所有 数系的扩充和 复数. 直接利用复数 的乘法运算法 则,求解即可. 解:复数 i(1+i )=﹣1+i, 解答: 点评: 所求复数的实 部为:﹣1. 故答案为:﹣1. 本题考查复数 的基本运算,复 数的基本概念, 第 14 页(共 33 页) 第 15 页 共 33 页 考查计算能力. 10.(5 分)(2015•北京)2﹣3,3 ,log25 三个数中最大数的是 log25 . 考点: 专题: 分析: 不等式比较大 小.菁优网版权所有 函数的性质及 应用. 运用指数函数 和对数函数的 单调性,可得 0 <2﹣3<1,1<3 <2,log25> log24=2,即可得 到最大数. 解答: 解:由于 0< 2﹣3<1,1<3 <2, log25>log24=2 ,则三个数中最 大的数为 log25 .故答案为:log25 .点评: 本题考查数的 大小比较,主要 考查指数函数 和对数函数的 单调性的运用, 属于基础题. 11.(5 分)(2015•北京)在△ABC 中,a=3,b= ,∠A= ,则∠B= . 考点: 专题: 分析: 正弦定理.菁优网版权所有 解三角形. 由正弦定理可 得 sinB,再由三 角形的边角关 系,即可得到角 第 15 页(共 33 页) 第 16 页 共 33 页 B. 解答: 解:由正弦定理 可得, =,即有 sinB= ==,由 b<a,则 B< A, 可得 B= .故答案为: .点评: 本题考查正弦 定理的运用,同 时考查三角形 的边角关系,属 于基础题. 12.(5 分)(2015•北京)已知(2,0)是双曲线 x2﹣ =1(b>0)的一个焦点,则 b= .考点: 专题: 双曲线的简单 性质.菁优网版权所有 圆锥曲线的定 义、性质与方程 .分析: 求得双曲线 x2﹣ =1(b> 0)的焦点为( ,0),( ﹣,0), 可得 b 的方程, 即可得到 b 的 第 16 页(共 33 页) 第 17 页 共 33 页 值. 解:双曲线 x2﹣ 解答: =1(b>0) 的焦点为( ,0),( ﹣,0), 由题意可得 =2, 解得 b= .故答案为: 本题考查双曲 线的方程和性 .点评: 质,主要考查双 曲线的焦点的 求法,属于基础 题. 13.(5 分)(2015•北京)如图,△ABC 及其内部的点组成的集合记为 D,P(x,y)为 D 中任意一点,则 z=2x+3y 的最大值为 7 . 考点: 专题: 分析: 简单线性规划. 菁优网版权所有 不等式的解法 及应用. 利用线性规划 的知识,通过平 移即可求 z 的 最大值. 解答: 解:由 z=2x+3y, 第 17 页(共 33 页) 第 18 页 共 33 页 得 y= ,平移直线 y= ,由图 象可知当直线 y= 经过点 A 时,直线 y= 的截距最大,此时 z 最大. 即 A(2,1). 此时 z 的最大 值为 z=2×2+3×1=7, 故答案为:7. 点评: 本题主要考查 线性规划的应 用,利用数形结 合是解决线性 规划题目的常 用方法. 14.(5 分)(2015•北京)高三年级 267 位学生参加期末考试,某班 37 位学生的语文成绩 ,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生. 第 18 页(共 33 页) 第 19 页 共 33 页 从这次考试成绩看, ①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是 乙 ; ②在语文和数学系两个科目中,丙同学的成绩名次更靠前的科目是 数学 . 考点: 两个变量的线 性相关.菁优网版权所有 专题: 分析: 概率与统计. 根据散点图分 析三位同学总 成绩名次,语文 、数学名次. 解:由高三年级 267 位学生参加 期末考试,某班 37 位学生的语 文成绩,数学成 绩与总成绩在 全年级的排名 情况的散点图 可知 解答: ①在甲、乙两人 中,其语文成绩 名次比其总成 绩名次靠前的 学生是 乙; ②在语文和数 学两个科目中, 丙同学的成绩 名次更靠前的 科目是数学; 故答案为:乙; 数学. 点评: 本题考查了对 散点图的认识; 第 19 页(共 33 页) 第 20 页 共 33 页 属于基础题. 三、解答题(共 80 分) 15.(13 分)(2015•北京)已知函数 f(x)=sinx﹣2 sin2 (1)求 f(x)的最小正周期; (2)求 f(x)在区间[0, ]上的最小值. 考点: 三角函数的周 期性及其求法; 两角和与差的 正弦函数;三角 函数的最值.菁优网版权所有 三角函数的图 像与性质. 专题: 分析: (1)由三角函 数恒等变换化 简函数解析式 可得 f(x) =2sin(x+ )﹣,由三角 函数的周期性 及其求法即可 得解; (2)由 x∈[0, ],可求范围 x+ ∈[ ,π], 即可求得 f(x) 的取值范围,即 可得解. 解答: 解:(1)∵f(x )=sinx﹣2 sin2 =sinx﹣2 ×=sinx+ cosx ﹣第 20 页(共 33 页) 第 21 页 共 33 页 =2sin(x+ )﹣∴f(x)的最小 正周期 T= =2π; (2)∵x∈[0, ], ∴x+ ∈[ ,π], ∴sin(x+ )∈[0,1],即有:f (x)=2sin(x+ )﹣ ∈[﹣ ,2﹣ ], ∴可解得 f(x) 在区间[0, ]上的最小 值为:﹣ .点评: 本题主要考查 了三角函数恒 等变换的应用, 三角函数的周 期性及其求法, 三角函数的最 值的应用,属于 基本知识的考 查. 16.(13 分)(2015•北京)已知等差数列{an}满足 a1+a2=10,a4﹣a3=2 (1)求{an}的通项公式; (2)设等比数列{bn}满足 b2=a3,b3=a7,问:b6 与数列{an}的第几项相等? 考点: 专题: 分析: 等差数列的性 质.菁优网版权所有 计算题;等差数 列与等比数列. (I)由 a4﹣a3=2,可求 第 21 页(共 33 页) 第 22 页 共 33 页 公差 d,然后由 a1+a2=10,可求 a1,结合等差数 列的通项公式 可求 (II)由 b2=a3=8, b3=a7=16,可求 等比数列的首 项及公比,代入 等比数列的通 项公式可求 b6, 结合(I)可求 解:(I)设等差 数列{an}的公差 为 d. 解答: ∵a4﹣a3=2,所以 d=2 ∵a1+a2=10,所以 2a1+d=10 ∴a1=4, ∴an=4+2(n﹣1 )=2n+2(n=1, 2,…) (II)设等比数 列{bn}的公比为 q, ∵b2=a3=8, b3=a7=16, ∴∴q=2,b1=4 ∴=128,而 128=2n+2 ∴n=63 ∴b6 与数列{an} 中的第 63 项相 等点评: 本题主要考查 了等差数列与 第 22 页(共 33 页) 第 23 页 共 33 页 等比数列通项 公式的简单应 用,属于对基本 公式应用的考 查,试题比较容 易. 17.(13 分)(2015•北京)某超市随机选取 1000 位顾客,记录了他们购买甲、乙、丙、 丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买. 甲√乙×丙√丁√100 217 200 300 85 ×√×√√√√×√×√×√××××√××98 (1)估计顾客同时购买乙和丙的概率; (2)估计顾客在甲、乙、丙、丁中同时购买 3 种商品的概率; (3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大? 考点: 相互独立事件 的概率乘法公 式.菁优网版权所有 专题: 分析: 概率与统计. (1)从统计表 可得,在这 1000 名顾客中,同时 购买乙和丙的 有 200 人,从而 求得顾客同时 购买乙和丙的 概率. (2)根据在甲、 乙、丙、丁中同 时购买 3 种商 品的有 300 人, 求得顾客顾客 在甲、乙、丙、 丁中同时购买 3 种商品的概率 .(3)在这 1000 名顾客中,求出 同时购买甲和 第 23 页(共 33 页) 第 24 页 共 33 页 乙的概率、同时 购买甲和丙的 概率、同时购买 甲和丁的概率, 从而得出结论. 解:(1)从统 计表可得,在这 1000 名顾客中, 同时购买乙和 解答: 丙的有 200 人, 故顾客同时购 买乙和丙的概 率为 =0.2. (2)在这 1000 名顾客中,在甲 、乙、丙、丁中 同时购买 3 种 商品的有 100+200=300( 人), 故顾客顾客在 甲、乙、丙、丁 中同时购买 3 种商品的概率 为=0.3. (3)在这 1000 名顾客中,同时 购买甲和乙的 概率为 =0.2, 同时购买甲和 丙的概率为 =0.6, 同时购买甲和 丁的概率为 =0.1, 故同时购买甲 和丙的概率最 第 24 页(共 33 页) 第 25 页 共 33 页 大. 点评: 本题主要考查 古典概率、互斥 事件的概率加 法公式的应用, 属于基础题. 18.(14 分)(2015•北京)如图,在三棱锥 V﹣ABC 中,平面 VAB⊥平面 ABC,△VAB 为等边三角形,AC⊥BC 且 AC=BC= ,O,M 分别为 AB,VA 的中点. (1)求证:VB∥平面 MOC; (2)求证:平面 MOC⊥平面 VAB (3)求三棱锥 V﹣ABC 的体积. 考点: 棱柱、棱锥、棱 台的体积;直线 与平面平行的 判定;平面与平 面垂直的判定. 菁优网版权所有 专题: 分析: 综合题;空间位 置关系与距离. (1)利用三角 形的中位线得 出 OM∥VB,利 用线面平行的 判定定理证明 VB∥平面 MOC ;(2)证明:OC⊥ 平面 VAB,即 可证明平面 MOC⊥平面 VAB (3)利用等体 积法求三棱锥 V﹣ABC 的体 积. 第 25 页(共 33 页) 第 26 页 共 33 页 解答: (1)证明:∵O, M 分别为 AB, VA 的中点, ∴OM∥VB, ∵VB⊄平面 MOC,OM⊂平 面 MOC, ∴VB∥平面 MOC; (2)∵AC=BC, O 为 AB 的中 点, ∴OC⊥AB, ∵平面 VAB⊥平 面 ABC,OC⊂ 平面 ABC, ∴OC⊥平面 VAB, ∵OC⊂平面 MOC, ∴平面 MOC⊥平 面 VAB (3)在等腰直 角三角形 ACB 中,AC=BC= ,∴AB=2,OC=1 ,∴S△VAB =,∵OC⊥平面 VAB, ∴VC﹣VAB •S△VAB ==,∴VV﹣ABC=VC﹣ =.VAB 点评: 本题考查线面 平行的判定,考 查平面与平面 垂直的判定,考 查体积的计算, 正确运用线面 平行、平面与平 第 26 页(共 33 页) 第 27 页 共 33 页 面垂直的判定 定理是关键. 19.(13 分)(2015•北京)设函数 f(x)= ﹣klnx,k>0. (1)求 f(x)的单调区间和极值; (2)证明:若 f(x)存在零点,则 f(x)在区间(1, )上仅有一个零点. 考点: 利用导数研究 函数的单调性; 利用导数研究 函数的极值.菁优网版权所有 导数的综合应 用. 专题: 分析: (1)利用 f’(x )≥0 或 f’(x) ≤0 求得函数的 单调区间并能 求出极值; (2)利用函数 的导数的极值 求出最值,利用 最值讨论存在 零点的情况. 解:(1)由 f( x)= 解答: f’(x)=x﹣ 由 f’(x)=0 解 得 x= f(x)与 f’(x) 在区间(0,+∞ )上的情况如下 :Xf’(x) f(x) 所以,f(x)的 单调递增区间 第 27 页(共 33 页) 第 28 页 共 33 页 为( ), 单调递减区间 为(0, ); f(x)在 x= 处的极小值为 f ()= .(2)证明:由( 1)知,f(x)在 区间(0,+∞) 上的最小值为 f ()= .因为 f(x)存在 零点,所以 ,从而 k≥e 当 k=e 时,f(x) 在区间(1, 上单调递减,且 f )=0 )(所以 x= 是 f (x)在区间(1 ,]上唯一零 点. 当 k>e 时,f(x) 在区间(0, )上单调递减, 且,所以 f(x)在区 间(1, ]上仅 有一个零点. 综上所述,若 f (x)存在零点, 则 f(x)在区间 (1, ]上仅 第 28 页(共 33 页) 第 29 页 共 33 页 有一个零点. 本题考查利用 函数的导数求 单调区间和导 数的综合应用, 在高考中属于 常见题型. 点评: 20.(14 分)(2015•北京)已知椭圆 C:x2+3y2=3,过点 D(1,0)且不过点 E(2,1) 的直线与椭圆 C 交于 A,B 两点,直线 AE 与直线 x=3 交于点 M. (1)求椭圆 C 的离心率; (2)若 AB 垂直于 x 轴,求直线 BM 的斜率; (3)试判断直线 BM 与直线 DE 的位置关系,并说明理由. 考点: 直线与圆锥曲 线的综合问题; 椭圆的标准方 程.菁优网版权所有 专题: 分析: 圆锥曲线的定 义、性质与方程 .(1)通过将椭 圆 C 的方程化 成标准方程,利 用离心率计算 公式即得结论; (2)通过令直 线 AE 的方程中 x=3,得点 M 坐 标,即得直线 BM 的斜率; (3)分直线 AB 的斜率不存 在与存在两种 情况讨论,利用 韦达定理,计算 即可. 解答: 解:(1)∵椭圆 C:x2+3y2=3, ∴椭圆 C 的标准 方程为: +y2=1, ∴a= ,b=1,c= 第 29 页(共 33 页) 第 30 页 共 33 页 ,∴椭圆 C 的离心 率 e= = ;(2)∵AB 过点 D(1,0)且垂 直于 x 轴, ∴可设 A(1,y1) ,B(1,﹣y1) ,∵E(2,1),∴ 直线 AE 的方程 为:y﹣1=( 1﹣y1)(x﹣2), 令 x=3,得 M(3 ,2﹣y1), ∴直线 BM 的斜 率 kBM ==1; (3)结论:直 线 BM 与直线 DE 平行. 证明如下: 当直线 AB 的 斜率不存在时, 由(2)知 kBM=1, 又∵直线 DE 的 斜率 kDE ==1, ∴BM∥DE; 当直线 AB 的 斜率存在时,设 其方程为 y=k( x﹣1)(k≠1), 设 A(x1,y1),B (x2,y2), 则直线 AE 的方 程为 y﹣1= (x﹣2) 第 30 页(共 33 页) 第 31 页 共 33 页 ,令 x=3,则点 M (3, ), ∴直线 BM 的斜 率 kBM =,联立 ,得(1+3k2) x2﹣6k2x+3k2﹣ 3=0, 由韦达定理,得 x1+x2= ,x1x2= ,∵kBM﹣1= ===0, ∴kBM=1=kDE ,即 BM∥DE; 综上所述,直线 第 31 页(共 33 页) 第 32 页 共 33 页 BM 与直线 DE 平行. 点评: 本题是一道直 线与椭圆的综 合题,涉及到韦 达定理等知识, 考查计算能力, 注意解题方法 的积累,属于中 档题. 第 32 页(共 33 页) 第 33 页 共 33 页 第 33 页(共 33 页)
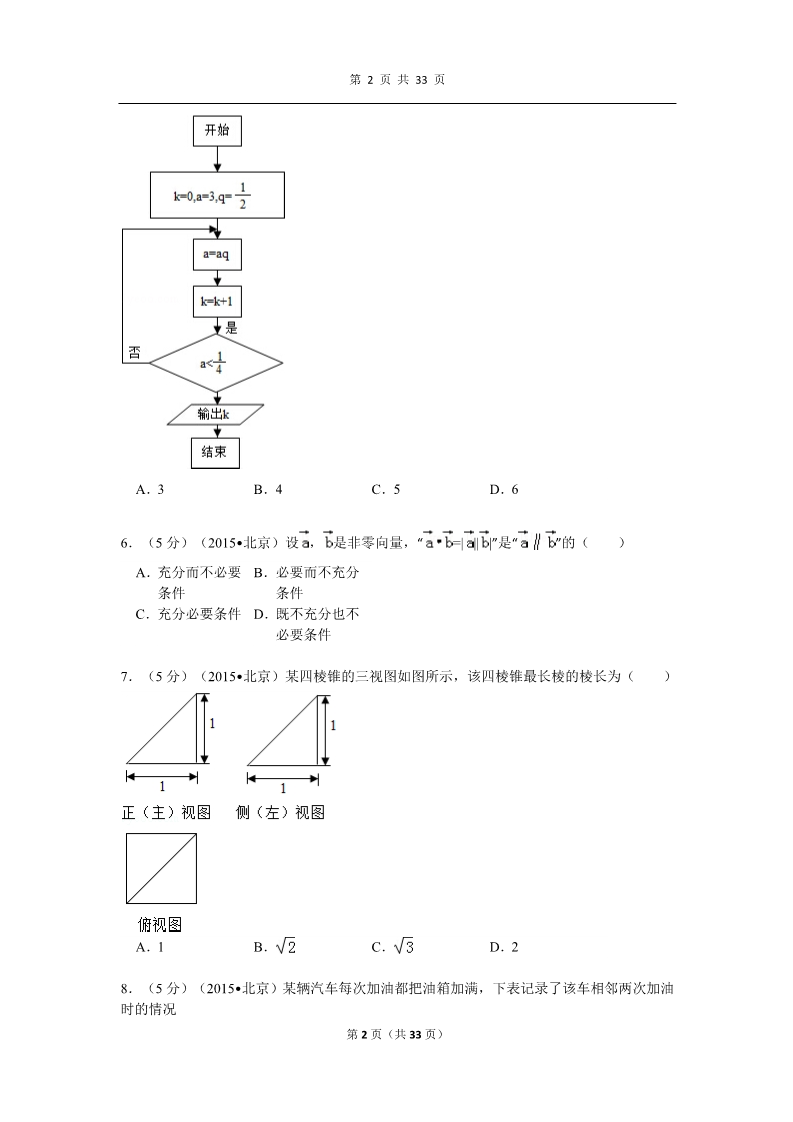
第 1 页 共 33 页 2015 年北京市高考数学试卷(文科) 一、选择题(每小题 5 分,共 40 分) 1.(5 分)(2015•北京)若集合 A={x|﹣5<x<2},B={x|﹣3<x<3},则 A∩B=( ) {x|﹣3<x<2} A. {x|﹣5<x<2} B. {x|﹣3<x<3} C. {x|﹣5<x<3} D. 2.(5 分)(2015•北京)圆心为(1,1)且过原点的圆的方程是( ) (x﹣1)2+( y﹣1)2=1 (x﹣1)2+( y﹣1)2=2 22 A. B. C. D. B(x+1) +( y+1)2=1 (x+1) +(y+1 )2=2 3.(5 分)(2015•北京)下列函数中为偶函数的是( ) y=2﹣x 22 A. y=x sinx B. y=x cosx C.y=|lnx| D. 4.(5 分)(2015•北京)某校老年、中年和青年教师的人数见下表,采用分层插样的方法 调查教师的身体状况,在抽取的样本中,青年教师有 320 人,则该样本的老年教师人数为( )类别 人数 900 老年教师 中年教师 青年教师 合计 1800 1600 4300 A.90 B.100 C.180 D.300 5.(5 分)(2015•北京)执行如图所示的程序框图,输出的 k 值为( ) 第 1 页(共 33 页) 第 2 页 共 33 页 A.3 B.4 C.5 D.6 6.(5 分)(2015•北京)设 , 是非零向量,“ A.充分而不必要 B.必要而不充分 =| || |”是“ ”的( ) 条件 条件 C.充分必要条件 D.既不充分也不 必要条件 7.(5 分)(2015•北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) A.1 B. C. D.2 8.(5 分)(2015•北京)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油 时的情况 第 2 页(共 33 页) 第 3 页 共 33 页 加油时间 加油量(升) 加油时的累计 里程(千米) 2015 年 5 月 1 12 35000 日2015 年 5 月 15 48 35600 日注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每 100 千米平均耗 油量为 ( ) A.6 升 B.8 升 C.10 升 D.12 升 二、填空题 9.(5 分)(2015•北京)复数 i(1+i)的实部为 . 10.(5 分)(2015•北京)2﹣3,3 ,log25 三个数中最大数的是 . 11.(5 分)(2015•北京)在△ABC 中,a=3,b= ,∠A= ,则∠B= . 12.(5 分)(2015•北京)已知(2,0)是双曲线 x2﹣ =1(b>0)的一个焦点,则 b= . 13.(5 分)(2015•北京)如图,△ABC 及其内部的点组成的集合记为 D,P(x,y)为 D 中任意一点,则 z=2x+3y 的最大值为 . 14.(5 分)(2015•北京)高三年级 267 位学生参加期末考试,某班 37 位学生的语文成绩 ,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生. 第 3 页(共 33 页) 第 4 页 共 33 页 从这次考试成绩看, ①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是 ; ②在语文和数学系两个科目中,丙同学的成绩名次更靠前的科目是 . 三、解答题(共 80 分) 15.(13 分)(2015•北京)已知函数 f(x)=sinx﹣2 sin2 (1)求 f(x)的最小正周期; (2)求 f(x)在区间[0, ]上的最小值. 16.(13 分)(2015•北京)已知等差数列{an}满足 a1+a2=10,a4﹣a3=2 (1)求{an}的通项公式; (2)设等比数列{bn}满足 b2=a3,b3=a7,问:b6 与数列{an}的第几项相等? 17.(13 分)(2015•北京)某超市随机选取 1000 位顾客,记录了他们购买甲、乙、丙、 丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买. 甲√乙×丙√丁√100 217 200 300 85 ×√×√√√√×√×√×√××××√××98 (1)估计顾客同时购买乙和丙的概率; (2)估计顾客在甲、乙、丙、丁中同时购买 3 种商品的概率; (3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大? 18.(14 分)(2015•北京)如图,在三棱锥 V﹣ABC 中,平面 VAB⊥平面 ABC,△VAB 为等边三角形,AC⊥BC 且 AC=BC= ,O,M 分别为 AB,VA 的中点. (1)求证:VB∥平面 MOC; (2)求证:平面 MOC⊥平面 VAB (3)求三棱锥 V﹣ABC 的体积. 第 4 页(共 33 页) 第 5 页 共 33 页 19.(13 分)(2015•北京)设函数 f(x)= ﹣klnx,k>0. (1)求 f(x)的单调区间和极值; (2)证明:若 f(x)存在零点,则 f(x)在区间(1, )上仅有一个零点. 20.(14 分)(2015•北京)已知椭圆 C:x2+3y2=3,过点 D(1,0)且不过点 E(2,1) 的直线与椭圆 C 交于 A,B 两点,直线 AE 与直线 x=3 交于点 M. (1)求椭圆 C 的离心率; (2)若 AB 垂直于 x 轴,求直线 BM 的斜率; (3)试判断直线 BM 与直线 DE 的位置关系,并说明理由. 第 5 页(共 33 页) 第 6 页 共 33 页 2015 年北京市高考数学试卷(文科) 参考答案与试题解析 一、选择题(每小题 5 分,共 40 分) 1.(5 分)(2015•北京)若集合 A={x|﹣5<x<2},B={x|﹣3<x<3},则 A∩B=( ) {x|﹣3<x<2} A. {x|﹣5<x<2} B. {x|﹣3<x<3} C. {x|﹣5<x<3} D. 考点: 交集及其运算. 菁优网版权所有 专题: 分析: 集合. 直接利用集合 的交集的运算 法则求解即可. 解:集合 解答: A={x|﹣5<x< 2},B={x|﹣3< x<3}, 则 A∩B={x|﹣3 <x<2}. 故选:A. 点评: 本题考查集合 的交集的运算 法则,考查计算 能力. 2.(5 分)(2015•北京)圆心为(1,1)且过原点的圆的方程是( ) (x﹣1)2+( A. (x﹣1)2+( D. 22B. C. B(x+1) +( y+1)2=1 (x+1) +(y+1 )2=2 y﹣1)2=1 y﹣1)2=2 考点: 专题: 分析: 圆的标准方程. 菁优网版权所有 计算题;直线与 圆. 利用两点间距 离公式求出半 径,由此能求出 圆的方程. 解答: 解:由题意知圆 半径 r= ,∴圆的方程为( x﹣1)2+(y﹣1 )2=2. 第 6 页(共 33 页) 第 7 页 共 33 页 故选:D. 点评: 本题考查圆的 方程的求法,解 题时要认真审 题,注意圆的方 程的求法,是基 础题. 3.(5 分)(2015•北京)下列函数中为偶函数的是( ) y=2﹣x D. 22 A. y=x sinx B. y=x cosx C.y=|lnx| 考点: 函数奇偶性的 判断.菁优网版权所有 专题: 分析: 函数的性质及 应用. 首先从定义域 上排除选项 C, 然后在其他选 项中判断﹣x 与 x 的函数值 关系,相等的就 是偶函数. 解答: 解:对于 A,( 2﹣x) sin(﹣x) =﹣x2sinx;是 奇函数; 对于 B,(﹣x) 2cos(﹣x) =x2cosx;是偶 函数; 对于 C,定义域 为(0,+∞), 是非奇非偶的 函数; 对于 D,定义域 为 R,但是 2﹣( ﹣x)=2x≠2﹣x ,2x≠﹣2﹣x;是非 奇非偶的函数; 故选 B 点评: 本题考查了函 数奇偶性的判 第 7 页(共 33 页) 第 8 页 共 33 页 断;首先判断定 义域是否关于 原点对称;如果 不对称,函数是 非奇非偶的函 数;如果对称, 再判断 f(﹣x) 与 f(x) 关系, 相等是偶函数, 相反是奇函数. 4.(5 分)(2015•北京)某校老年、中年和青年教师的人数见下表,采用分层插样的方法 调查教师的身体状况,在抽取的样本中,青年教师有 320 人,则该样本的老年教师人数为( )类别 人数 900 老年教师 中年教师 青年教师 合计 1800 1600 4300 A.90 考点: 专题: 分析: B.100 C.180 D.300 分层抽样方法. 菁优网版权所有 计算题;概率与 统计. 由题意,老年和 青年教师的人 数比为 900: 1600=9:16,即 可得出结论. 解:由题意,老 年和青年教师 的人数比为 900 :1600=9:16, 因为青年教师 有 320 人,所以 老年教师有 180 人, 解答: 故选:C. 点评: 本题考查分层 抽样,考查学生 的计算能力,比 较基础. 第 8 页(共 33 页) 第 9 页 共 33 页 5.(5 分)(2015•北京)执行如图所示的程序框图,输出的 k 值为( ) A.3 B.4 C.5 D.6 考点: 专题: 程序框图.菁优网版权所有 图表型;算法和 程序框图. 分析: 模拟执行程序 框图,依次写出 每次循环得到 的 a,k 的值, 当 a= 时满足 条件 a< ,退 出循环,输出 k 的值为 4. 解答: 解:模拟执行程 序框图,可得 k=0,a=3,q= a= ,k=1 不满足条件 a< ,a= ,k=2 第 9 页(共 33 页) 第 10 页 共 33 页 不满足条件 a< ,a= ,k=3 不满足条件 a< ,a= ,k=4 满足条件 a< , 退出循环,输出 k 的值为 4. 故选:B. 点评: 本题主要考查 了循环结构的 程序框图,属于 基础题. 6.(5 分)(2015•北京)设 , 是非零向量,“ A.充分而不必要 B.必要而不充分 =| || |”是“ ”的( ) 条件 条件 C.充分必要条件 D.既不充分也不 必要条件 考点: 必要条件、充分 条件与充要条 件的判断;平面 向量数量积的 运算.菁优网版权所有 专题: 分析: 平面向量及应 用;简易逻辑. 由便可得到 夹角为 0,从而 得到 ∥ ,而 ∥ 并不能得到 夹角为 0,从而 得不到 ,这样根据充分 条件、必要条件 第 10 页(共 33 页) 第 11 页 共 33 页 的概念即可找 出正确选项. 解:(1) 解答: ;∴时,cos =1; ∴;∴ ∥ ; ∴“ ”是“ ∥ ”的充分 条件; (2) ∥ 时, 的夹角为 0 或 π; ∴,或﹣ ;即 ∥ 得不到 ;∴“ ”不是“ ∥ ”的必 要条件; ∴总上可得“ 第 11 页(共 33 页) 第 12 页 共 33 页 ”是“ ∥ ”的充分 不必要条件. 故选 A. 点评: 考查充分条件, 必要条件,及充 分不必要条件 的概念,以及判 断方法与过程, 数量积的计算 公式,向量共线 的定义,向量夹 角的定义. 7.(5 分)(2015•北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) A.1 考点: 专题: 分析: B. C. D.2 由三视图求面 积、体积.菁优网版权所有 空间位置关系 与距离. 几何体是四棱 锥,且四棱锥的 一条侧棱与底 面垂直,结合直 观图求相关几 何量的数据,可 得答案 解答: 解:由三视图知 :几何体是四棱 锥,且四棱锥的 一条侧棱与底 第 12 页(共 33 页) 第 13 页 共 33 页 面垂直, 底面为正方形 如图: 其中 PA⊥平面 ABCD,底面 ABCD 为正方 形∴PA=1,AB=1, AD=1, ∴PB= ,PC= =.PD= 该几何体最长 棱的棱长为: 故选:C. 点评: 本题考查了由 三视图求几何 体的最长棱长 问题,根据三视 图判断几何体 的结构特征是 解答本题的关 键 8.(5 分)(2015•北京)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油 时的情况 加油时间 加油量(升) 加油时的累计 里程(千米) 2015 年 5 月 1 12 35000 日2015 年 5 月 15 48 35600 日注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每 100 千米平均耗 油量为 ( ) A.6 升 B.8 升 C.10 升 D.12 升 第 13 页(共 33 页) 第 14 页 共 33 页 考点: 专题: 分析: 一次函数的性 质与图象.菁优网版权所有 函数的性质及 应用. 由表格信息,得 到该车加了 48 升的汽油,跑了 600 千米,由此 得到该车每 100 千米平均耗油 量. 解答: 解:由表格信息 ,得到该车加了 48 升的汽油,跑 了 600 千米,所 以该车每 100 千米平均耗油 量 48÷6=8; 故选:B. 点评: 本题考查了学 生对表格的理 解以及对数据 信息的处理能 力. 二、填空题 9.(5 分)(2015•北京)复数 i(1+i)的实部为 ﹣1 . 考点: 专题: 分析: 复数的基本概 念.菁优网版权所有 数系的扩充和 复数. 直接利用复数 的乘法运算法 则,求解即可. 解:复数 i(1+i )=﹣1+i, 解答: 点评: 所求复数的实 部为:﹣1. 故答案为:﹣1. 本题考查复数 的基本运算,复 数的基本概念, 第 14 页(共 33 页) 第 15 页 共 33 页 考查计算能力. 10.(5 分)(2015•北京)2﹣3,3 ,log25 三个数中最大数的是 log25 . 考点: 专题: 分析: 不等式比较大 小.菁优网版权所有 函数的性质及 应用. 运用指数函数 和对数函数的 单调性,可得 0 <2﹣3<1,1<3 <2,log25> log24=2,即可得 到最大数. 解答: 解:由于 0< 2﹣3<1,1<3 <2, log25>log24=2 ,则三个数中最 大的数为 log25 .故答案为:log25 .点评: 本题考查数的 大小比较,主要 考查指数函数 和对数函数的 单调性的运用, 属于基础题. 11.(5 分)(2015•北京)在△ABC 中,a=3,b= ,∠A= ,则∠B= . 考点: 专题: 分析: 正弦定理.菁优网版权所有 解三角形. 由正弦定理可 得 sinB,再由三 角形的边角关 系,即可得到角 第 15 页(共 33 页) 第 16 页 共 33 页 B. 解答: 解:由正弦定理 可得, =,即有 sinB= ==,由 b<a,则 B< A, 可得 B= .故答案为: .点评: 本题考查正弦 定理的运用,同 时考查三角形 的边角关系,属 于基础题. 12.(5 分)(2015•北京)已知(2,0)是双曲线 x2﹣ =1(b>0)的一个焦点,则 b= .考点: 专题: 双曲线的简单 性质.菁优网版权所有 圆锥曲线的定 义、性质与方程 .分析: 求得双曲线 x2﹣ =1(b> 0)的焦点为( ,0),( ﹣,0), 可得 b 的方程, 即可得到 b 的 第 16 页(共 33 页) 第 17 页 共 33 页 值. 解:双曲线 x2﹣ 解答: =1(b>0) 的焦点为( ,0),( ﹣,0), 由题意可得 =2, 解得 b= .故答案为: 本题考查双曲 线的方程和性 .点评: 质,主要考查双 曲线的焦点的 求法,属于基础 题. 13.(5 分)(2015•北京)如图,△ABC 及其内部的点组成的集合记为 D,P(x,y)为 D 中任意一点,则 z=2x+3y 的最大值为 7 . 考点: 专题: 分析: 简单线性规划. 菁优网版权所有 不等式的解法 及应用. 利用线性规划 的知识,通过平 移即可求 z 的 最大值. 解答: 解:由 z=2x+3y, 第 17 页(共 33 页) 第 18 页 共 33 页 得 y= ,平移直线 y= ,由图 象可知当直线 y= 经过点 A 时,直线 y= 的截距最大,此时 z 最大. 即 A(2,1). 此时 z 的最大 值为 z=2×2+3×1=7, 故答案为:7. 点评: 本题主要考查 线性规划的应 用,利用数形结 合是解决线性 规划题目的常 用方法. 14.(5 分)(2015•北京)高三年级 267 位学生参加期末考试,某班 37 位学生的语文成绩 ,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生. 第 18 页(共 33 页) 第 19 页 共 33 页 从这次考试成绩看, ①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是 乙 ; ②在语文和数学系两个科目中,丙同学的成绩名次更靠前的科目是 数学 . 考点: 两个变量的线 性相关.菁优网版权所有 专题: 分析: 概率与统计. 根据散点图分 析三位同学总 成绩名次,语文 、数学名次. 解:由高三年级 267 位学生参加 期末考试,某班 37 位学生的语 文成绩,数学成 绩与总成绩在 全年级的排名 情况的散点图 可知 解答: ①在甲、乙两人 中,其语文成绩 名次比其总成 绩名次靠前的 学生是 乙; ②在语文和数 学两个科目中, 丙同学的成绩 名次更靠前的 科目是数学; 故答案为:乙; 数学. 点评: 本题考查了对 散点图的认识; 第 19 页(共 33 页) 第 20 页 共 33 页 属于基础题. 三、解答题(共 80 分) 15.(13 分)(2015•北京)已知函数 f(x)=sinx﹣2 sin2 (1)求 f(x)的最小正周期; (2)求 f(x)在区间[0, ]上的最小值. 考点: 三角函数的周 期性及其求法; 两角和与差的 正弦函数;三角 函数的最值.菁优网版权所有 三角函数的图 像与性质. 专题: 分析: (1)由三角函 数恒等变换化 简函数解析式 可得 f(x) =2sin(x+ )﹣,由三角 函数的周期性 及其求法即可 得解; (2)由 x∈[0, ],可求范围 x+ ∈[ ,π], 即可求得 f(x) 的取值范围,即 可得解. 解答: 解:(1)∵f(x )=sinx﹣2 sin2 =sinx﹣2 ×=sinx+ cosx ﹣第 20 页(共 33 页) 第 21 页 共 33 页 =2sin(x+ )﹣∴f(x)的最小 正周期 T= =2π; (2)∵x∈[0, ], ∴x+ ∈[ ,π], ∴sin(x+ )∈[0,1],即有:f (x)=2sin(x+ )﹣ ∈[﹣ ,2﹣ ], ∴可解得 f(x) 在区间[0, ]上的最小 值为:﹣ .点评: 本题主要考查 了三角函数恒 等变换的应用, 三角函数的周 期性及其求法, 三角函数的最 值的应用,属于 基本知识的考 查. 16.(13 分)(2015•北京)已知等差数列{an}满足 a1+a2=10,a4﹣a3=2 (1)求{an}的通项公式; (2)设等比数列{bn}满足 b2=a3,b3=a7,问:b6 与数列{an}的第几项相等? 考点: 专题: 分析: 等差数列的性 质.菁优网版权所有 计算题;等差数 列与等比数列. (I)由 a4﹣a3=2,可求 第 21 页(共 33 页) 第 22 页 共 33 页 公差 d,然后由 a1+a2=10,可求 a1,结合等差数 列的通项公式 可求 (II)由 b2=a3=8, b3=a7=16,可求 等比数列的首 项及公比,代入 等比数列的通 项公式可求 b6, 结合(I)可求 解:(I)设等差 数列{an}的公差 为 d. 解答: ∵a4﹣a3=2,所以 d=2 ∵a1+a2=10,所以 2a1+d=10 ∴a1=4, ∴an=4+2(n﹣1 )=2n+2(n=1, 2,…) (II)设等比数 列{bn}的公比为 q, ∵b2=a3=8, b3=a7=16, ∴∴q=2,b1=4 ∴=128,而 128=2n+2 ∴n=63 ∴b6 与数列{an} 中的第 63 项相 等点评: 本题主要考查 了等差数列与 第 22 页(共 33 页) 第 23 页 共 33 页 等比数列通项 公式的简单应 用,属于对基本 公式应用的考 查,试题比较容 易. 17.(13 分)(2015•北京)某超市随机选取 1000 位顾客,记录了他们购买甲、乙、丙、 丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买. 甲√乙×丙√丁√100 217 200 300 85 ×√×√√√√×√×√×√××××√××98 (1)估计顾客同时购买乙和丙的概率; (2)估计顾客在甲、乙、丙、丁中同时购买 3 种商品的概率; (3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大? 考点: 相互独立事件 的概率乘法公 式.菁优网版权所有 专题: 分析: 概率与统计. (1)从统计表 可得,在这 1000 名顾客中,同时 购买乙和丙的 有 200 人,从而 求得顾客同时 购买乙和丙的 概率. (2)根据在甲、 乙、丙、丁中同 时购买 3 种商 品的有 300 人, 求得顾客顾客 在甲、乙、丙、 丁中同时购买 3 种商品的概率 .(3)在这 1000 名顾客中,求出 同时购买甲和 第 23 页(共 33 页) 第 24 页 共 33 页 乙的概率、同时 购买甲和丙的 概率、同时购买 甲和丁的概率, 从而得出结论. 解:(1)从统 计表可得,在这 1000 名顾客中, 同时购买乙和 解答: 丙的有 200 人, 故顾客同时购 买乙和丙的概 率为 =0.2. (2)在这 1000 名顾客中,在甲 、乙、丙、丁中 同时购买 3 种 商品的有 100+200=300( 人), 故顾客顾客在 甲、乙、丙、丁 中同时购买 3 种商品的概率 为=0.3. (3)在这 1000 名顾客中,同时 购买甲和乙的 概率为 =0.2, 同时购买甲和 丙的概率为 =0.6, 同时购买甲和 丁的概率为 =0.1, 故同时购买甲 和丙的概率最 第 24 页(共 33 页) 第 25 页 共 33 页 大. 点评: 本题主要考查 古典概率、互斥 事件的概率加 法公式的应用, 属于基础题. 18.(14 分)(2015•北京)如图,在三棱锥 V﹣ABC 中,平面 VAB⊥平面 ABC,△VAB 为等边三角形,AC⊥BC 且 AC=BC= ,O,M 分别为 AB,VA 的中点. (1)求证:VB∥平面 MOC; (2)求证:平面 MOC⊥平面 VAB (3)求三棱锥 V﹣ABC 的体积. 考点: 棱柱、棱锥、棱 台的体积;直线 与平面平行的 判定;平面与平 面垂直的判定. 菁优网版权所有 专题: 分析: 综合题;空间位 置关系与距离. (1)利用三角 形的中位线得 出 OM∥VB,利 用线面平行的 判定定理证明 VB∥平面 MOC ;(2)证明:OC⊥ 平面 VAB,即 可证明平面 MOC⊥平面 VAB (3)利用等体 积法求三棱锥 V﹣ABC 的体 积. 第 25 页(共 33 页) 第 26 页 共 33 页 解答: (1)证明:∵O, M 分别为 AB, VA 的中点, ∴OM∥VB, ∵VB⊄平面 MOC,OM⊂平 面 MOC, ∴VB∥平面 MOC; (2)∵AC=BC, O 为 AB 的中 点, ∴OC⊥AB, ∵平面 VAB⊥平 面 ABC,OC⊂ 平面 ABC, ∴OC⊥平面 VAB, ∵OC⊂平面 MOC, ∴平面 MOC⊥平 面 VAB (3)在等腰直 角三角形 ACB 中,AC=BC= ,∴AB=2,OC=1 ,∴S△VAB =,∵OC⊥平面 VAB, ∴VC﹣VAB •S△VAB ==,∴VV﹣ABC=VC﹣ =.VAB 点评: 本题考查线面 平行的判定,考 查平面与平面 垂直的判定,考 查体积的计算, 正确运用线面 平行、平面与平 第 26 页(共 33 页) 第 27 页 共 33 页 面垂直的判定 定理是关键. 19.(13 分)(2015•北京)设函数 f(x)= ﹣klnx,k>0. (1)求 f(x)的单调区间和极值; (2)证明:若 f(x)存在零点,则 f(x)在区间(1, )上仅有一个零点. 考点: 利用导数研究 函数的单调性; 利用导数研究 函数的极值.菁优网版权所有 导数的综合应 用. 专题: 分析: (1)利用 f’(x )≥0 或 f’(x) ≤0 求得函数的 单调区间并能 求出极值; (2)利用函数 的导数的极值 求出最值,利用 最值讨论存在 零点的情况. 解:(1)由 f( x)= 解答: f’(x)=x﹣ 由 f’(x)=0 解 得 x= f(x)与 f’(x) 在区间(0,+∞ )上的情况如下 :Xf’(x) f(x) 所以,f(x)的 单调递增区间 第 27 页(共 33 页) 第 28 页 共 33 页 为( ), 单调递减区间 为(0, ); f(x)在 x= 处的极小值为 f ()= .(2)证明:由( 1)知,f(x)在 区间(0,+∞) 上的最小值为 f ()= .因为 f(x)存在 零点,所以 ,从而 k≥e 当 k=e 时,f(x) 在区间(1, 上单调递减,且 f )=0 )(所以 x= 是 f (x)在区间(1 ,]上唯一零 点. 当 k>e 时,f(x) 在区间(0, )上单调递减, 且,所以 f(x)在区 间(1, ]上仅 有一个零点. 综上所述,若 f (x)存在零点, 则 f(x)在区间 (1, ]上仅 第 28 页(共 33 页) 第 29 页 共 33 页 有一个零点. 本题考查利用 函数的导数求 单调区间和导 数的综合应用, 在高考中属于 常见题型. 点评: 20.(14 分)(2015•北京)已知椭圆 C:x2+3y2=3,过点 D(1,0)且不过点 E(2,1) 的直线与椭圆 C 交于 A,B 两点,直线 AE 与直线 x=3 交于点 M. (1)求椭圆 C 的离心率; (2)若 AB 垂直于 x 轴,求直线 BM 的斜率; (3)试判断直线 BM 与直线 DE 的位置关系,并说明理由. 考点: 直线与圆锥曲 线的综合问题; 椭圆的标准方 程.菁优网版权所有 专题: 分析: 圆锥曲线的定 义、性质与方程 .(1)通过将椭 圆 C 的方程化 成标准方程,利 用离心率计算 公式即得结论; (2)通过令直 线 AE 的方程中 x=3,得点 M 坐 标,即得直线 BM 的斜率; (3)分直线 AB 的斜率不存 在与存在两种 情况讨论,利用 韦达定理,计算 即可. 解答: 解:(1)∵椭圆 C:x2+3y2=3, ∴椭圆 C 的标准 方程为: +y2=1, ∴a= ,b=1,c= 第 29 页(共 33 页) 第 30 页 共 33 页 ,∴椭圆 C 的离心 率 e= = ;(2)∵AB 过点 D(1,0)且垂 直于 x 轴, ∴可设 A(1,y1) ,B(1,﹣y1) ,∵E(2,1),∴ 直线 AE 的方程 为:y﹣1=( 1﹣y1)(x﹣2), 令 x=3,得 M(3 ,2﹣y1), ∴直线 BM 的斜 率 kBM ==1; (3)结论:直 线 BM 与直线 DE 平行. 证明如下: 当直线 AB 的 斜率不存在时, 由(2)知 kBM=1, 又∵直线 DE 的 斜率 kDE ==1, ∴BM∥DE; 当直线 AB 的 斜率存在时,设 其方程为 y=k( x﹣1)(k≠1), 设 A(x1,y1),B (x2,y2), 则直线 AE 的方 程为 y﹣1= (x﹣2) 第 30 页(共 33 页) 第 31 页 共 33 页 ,令 x=3,则点 M (3, ), ∴直线 BM 的斜 率 kBM =,联立 ,得(1+3k2) x2﹣6k2x+3k2﹣ 3=0, 由韦达定理,得 x1+x2= ,x1x2= ,∵kBM﹣1= ===0, ∴kBM=1=kDE ,即 BM∥DE; 综上所述,直线 第 31 页(共 33 页) 第 32 页 共 33 页 BM 与直线 DE 平行. 点评: 本题是一道直 线与椭圆的综 合题,涉及到韦 达定理等知识, 考查计算能力, 注意解题方法 的积累,属于中 档题. 第 32 页(共 33 页) 第 33 页 共 33 页 第 33 页(共 33 页)
声明:如果本站提供的资源有问题或者不能下载,请点击页面底部的"联系我们";
本站提供的资源大部分来自网络收集整理,如果侵犯了您的版权,请联系我们删除。





