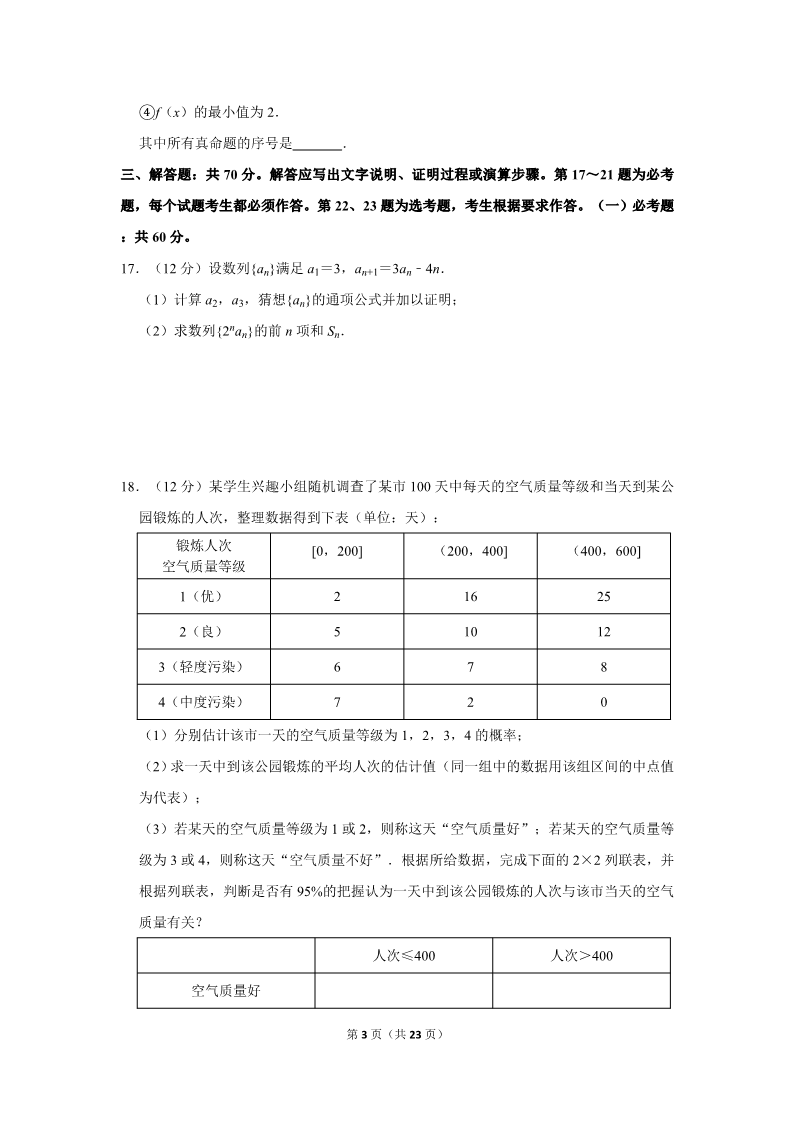
2020年全国统一高考数学试卷（理科）（新课标ⅲ）（含解析版）下载

2020 年全国统一高考数学试卷（理科）（新课标Ⅲ） 一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 1．（5 分）已知集合 A＝{（x，y）|x，y∈N*，y≥x}，B＝{（x，y）|x+y＝8}，则 A∩B 中 元素的个数为（　　） A．2 B．3 C．4 D．6 2．（5 分）复数 的虚部是（　　） A．﹣ B．﹣ C． D． 3．（5 分）在一组样本数据中，1，2，3，4 出现的频率分别为 p1，p2，p3，p4，且 1，则下面四种情形中，对应样本的标准差最大的一组是（　　） pi＝ A．p1＝p4＝0.1，p2＝p3＝0.4 C．p1＝p4＝0.2，p2＝p3＝0.3 B．p1＝p4＝0.4，p2＝p3＝0.1 D．p1＝p4＝0.3，p2＝p3＝0.2 4．（5 分）Logistic 模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数 据建立了某地区新冠肺炎累计确诊病例数 I（t）（t 的单位：天）的 Logistic 模型：I（t）＝ ，其中 K 为最大确诊病例数．当 I（t*）＝0.95K 时，标志着已初步遏制 疫情，则 t*约为（　　）（ln19≈3） A．60 B．63 C．66 D．69 5．（5 分）设 O 为坐标原点，直线 x＝2 与抛物线 C：y2＝2px（p＞0）交于 D，E 两点， 若 OD⊥OE，则 C 的焦点坐标为（　　） A．（ ，0） B．（ ，0） C．（1，0） D．（2，0） 6．（5 分）已知向量 ， 满足| |＝5，| |＝6， • ＝﹣6，则 cos＜ ， + ＞＝（　　） A．﹣ B．﹣ C． D． 7．（5 分）在△ABC 中，cosC＝ ，AC＝4，BC＝3，则 cosB＝（　　） A． B． C． D． 8．（5 分）如图为某几何体的三视图，则该几何体的表面积是（　　） 第 1 页（共 23 页） A．6+4 9．（5 分）已知 2tanθ﹣tan（θ+ A．﹣2 B．﹣1 B．4+4 C．6+2 D．4+2 D．2 ）＝7，则 tanθ＝（　　） C．1 10．（5 分）若直线 l 与曲线 y＝ 和圆x2+y2＝ 都相切，则l 的方程为（　　） A．y＝2x+1 B．y＝2x+ C．y＝ x+1 D．y＝ x+ 11．（5 分）设双曲线 C： ﹣＝1（a＞0，b＞0）的左、右焦点分别为 F1，F2，离心 率为 ．P 是 C 上一点，且 F1P⊥F2P．若△PF1F2 的面积为 4，则 a＝（　　） A．1 B．2 C．4 D．8 12．（5 分）已知 55＜84，134＜85．设 a＝log53，b＝log85，c＝log138，则（　　） A．a＜b＜c B．b＜a＜c C．b＜c＜a D．c＜a＜b 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．（5 分）若 x，y 满足约束条件 则 z＝3x+2y 的最大值为　 　． 14．（5 分）（x2+ ）6 的展开式中常数项是　 　（用数字作答）． 15．（5 分）已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的体积为　 　．16．（5 分）关于函数 f（x）＝sinx+ 有如下四个命题： ①f（x）的图象关于 y 轴对称． ②f（x）的图象关于原点对称． ③f（x）的图象关于直线 x＝ 对称． 第 2 页（共 23 页） ④f（x）的最小值为 2． 其中所有真命题的序号是　 　． 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17～21 题为必考 题，每个试题考生都必须作答。第 22、23 题为选考题，考生根据要求作答。（一）必考题 ：共 60 分。 17．（12 分）设数列{an}满足 a1＝3，an+1＝3an﹣4n． （1）计算 a2，a3，猜想{an}的通项公式并加以证明； （2）求数列{2nan}的前 n 项和 Sn． 18．（12 分）某学生兴趣小组随机调查了某市 100 天中每天的空气质量等级和当天到某公 园锻炼的人次，整理数据得到下表（单位：天）： 锻炼人次 [0，200] （200，400] （400，600] 空气质量等级 1（优） 256716 10 725 12 82（良） 3（轻度污染） 4（中度污染） 20（1）分别估计该市一天的空气质量等级为 1，2，3，4 的概率； （2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值 为代表）； （3）若某天的空气质量等级为 1 或 2，则称这天“空气质量好”；若某天的空气质量等 级为 3 或 4，则称这天“空气质量不好”．根据所给数据，完成下面的 2×2 列联表，并 根据列联表，判断是否有 95%的把握认为一天中到该公园锻炼的人次与该市当天的空气 质量有关？ 人次≤400 人次＞400 空气质量好 第 3 页（共 23 页） 空气质量不好 附：K2＝ P（K2≥k） 0.050 3.841 0.010 6.635 0.001 k10.828 19．（12 分）如图，在长方体 ABCD﹣A1B1C1D1 中，点 E，F 分别在棱 DD1，BB1 上，且 2DE ＝ED1，BF＝2FB1． （1）证明：点 C1 在平面 AEF 内； （2）若 AB＝2，AD＝1，AA1＝3，求二面角 A﹣EF﹣A1 的正弦值． 第 4 页（共 23 页） 20．（12 分）已知椭圆 C： +＝1（0＜m＜5）的离心率为 ，A，B 分别为 C 的左、 右顶点． （1）求 C 的方程； （2）若点 P 在 C 上，点 Q 在直线 x＝6 上，且|BP|＝|BQ|，BP⊥BQ，求△APQ 的面积． 21．（12 分）设函数 f（x）＝x3+bx+c，曲线 y＝f（x）在点（ ，f（ ））处的切线与y 轴垂直． （1）求 b； （2）若 f（x）有一个绝对值不大于 1 的零点，证明：f（x）所有零点的绝对值都不大于 1 ．（二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的 第一题计分。[选修 4-4：坐标系与参数方程]（10 分） 22．（10 分）在直角坐标系 xOy 中，曲线 C 的参数方程为 （t 为参数且 t≠1 ），C 与坐标轴交于 A，B 两点． （1）求|AB|； （2）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求直线 AB 的极坐标方程． 第 5 页（共 23 页） [选修 4-5：不等式选讲]（10 分） 23．设 a，b，c∈R，a+b+c＝0，abc＝1． （1）证明：ab+bc+ca＜0； （2）用 max{a，b，c}表示 a，b，c 的最大值，证明：max{a，b，c}≥ ．第 6 页（共 23 页） 2020 年全国统一高考数学试卷（理科）（新课标Ⅲ） 参考答案与试题解析 一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 1．（5 分）已知集合 A＝{（x，y）|x，y∈N*，y≥x}，B＝{（x，y）|x+y＝8}，则 A∩B 中 元素的个数为（　　） A．2 B．3 C．4 D．6 【分析】利用交集定义求出 A∩B＝{（7，1），（6，2），（5，3），（4，4）}．由此 能求出 A∩B 中元素的个数． 【解答】解：∵集合 A＝{（x，y）|x，y∈N*，y≥x}，B＝{（x，y）|x+y＝8}， ∴A∩B＝{（x，y）| }＝{（7，1），（6，2），（5，3），（4，4 ）}． ∴A∩B 中元素的个数为 4． 故选：C． 【点评】本题考查交集中元素个数的求法，考查交集定义等基础知识，考查运算求解能 力，是基础题． 2．（5 分）复数 A．﹣ 的虚部是（　　） B．﹣ C． D． 【分析】直接利用复数代数形式的乘除运算化简得答案． 【解答】解：∵ ＝，∴复数 的虚部是 ．故选：D． 【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题． 3．（5 分）在一组样本数据中，1，2，3，4 出现的频率分别为 p1，p2，p3，p4，且 pi＝ 1，则下面四种情形中，对应样本的标准差最大的一组是（　　） 第 7 页（共 23 页） A．p1＝p4＝0.1，p2＝p3＝0.4 C．p1＝p4＝0.2，p2＝p3＝0.3 B．p1＝p4＝0.4，p2＝p3＝0.1 D．p1＝p4＝0.3，p2＝p3＝0.2 【分析】根据题意，求出各组数据的方差，方差大的对应的标准差也大． 【解答】解：选项 A：E（x）＝1×0.1+2×0.4+3×0.4+4×0.1＝2.5，所以 D（x）＝（1﹣ 2.5）2×0.1+（2﹣2.5）2×0.4+（3﹣2.5）2×0.4+（4﹣2.5）2×0.1＝0.65； 同理选项 B：E（x）＝2.5，D（x）＝2.05； 选项 C：E（x）＝2.5，D（x）＝1.05； 选项 D：E（x）＝2.5，D（x）＝1.45； 故选：B． 【点评】本题考查了方差和标准差的问题，记住方差、标准差的公式是解题的关键． 4．（5 分）Logistic 模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数 据建立了某地区新冠肺炎累计确诊病例数 I（t）（t 的单位：天）的 Logistic 模型：I（t）＝ ，其中 K 为最大确诊病例数．当 I（t*）＝0.95K 时，标志着已初步遏制 疫情，则 t*约为（　　）（ln19≈3） A．60 B．63 C．66 D．69 【分析】根据所给材料的公式列出方程 【解答】解：由已知可得 ＝0.95K，解出 t 即可． ＝0.95K，解得 e﹣0.23（t﹣53） ＝，两边取对数有﹣0.23（t﹣53）＝﹣ln19， 解得 t≈66， 故选：C． 【点评】本题考查函数模型的实际应用，考查学生计算能力，属于中档题 5．（5 分）设 O 为坐标原点，直线 x＝2 与抛物线 C：y2＝2px（p＞0）交于 D，E 两点， 若 OD⊥OE，则 C 的焦点坐标为（　　） A．（ ，0） B．（ ，0） C．（1，0） D．（2，0） 【分析】利用已知条件转化求解 E、D 坐标，通过 kOD•kOE＝﹣1，求解抛物线方程，即 可得到抛物线的焦点坐标． 【解答】解：将 x＝2 代入抛物线 y2＝2px，可得 y＝±2 ，OD⊥OE，可得 kOD•kOE＝﹣ 1， 第 8 页（共 23 页） 即，解得 p＝1， 所以抛物线方程为：y2＝2x，它的焦点坐标（ ，0）． 故选：B． 【点评】本题考查抛物线的简单性质的应用，是基本知识的考查． 6．（5 分）已知向量 ， 满足| |＝5，| |＝6， • ＝﹣6，则 cos＜ ， + ＞＝（　　） A．﹣ B．﹣ C． D． 【分析】利用已知条件求出| |，然后利用向量的数量积求解即可． 【解答】解：向量 ， 满足| |＝5，| |＝6， • ＝﹣6， 可得| |＝ ＝＝7， cos＜ ， + ＞＝ 故选：D． ＝＝＝．【点评】本题考查平面向量的数量积的应用，数量积的运算以及向量的夹角的求法，是 中档题． 7．（5 分）在△ABC 中，cosC＝ ，AC＝4，BC＝3，则 cosB＝（　　） A． B． C． D． 【分析】先根据余弦定理求出 AB，再代入余弦定理求出结论． 【解答】解：在△ABC 中，cosC＝ ，AC＝4，BC＝3， 由余弦定理可得 AB2＝AC2+BC2﹣2AC•BC•cosC＝42+32﹣2×4×3× ＝9； 故 AB＝3； ∴cosB＝ ＝＝ ， 故选：A． 【点评】本题主要考查了余弦定理的应用，熟练掌握余弦定理是解本题的关键． 8．（5 分）如图为某几何体的三视图，则该几何体的表面积是（　　） 第 9 页（共 23 页） A．6+4 B．4+4 C．6+2 D．4+2 【分析】先由三视图画出几何体的直观图，利用三视图的数据，利用三棱锥的表面积公 式计算即可． 【解答】解：由三视图可知，几何体的直观图是正方体的一个角，如图： PA＝AB＝AC＝2，PA、AB、AC 两两垂直， 故 PB＝BC＝PC＝2 ，几何体的表面积为：3× 故选：C． ＝6+2 ，【点评】本题考查多面体的表面积的求法，几何体的三视图与直观图的应用，考查空间 想象能力，计算能力． 9．（5 分）已知 2tanθ﹣tan（θ+ A．﹣2 B．﹣1 ）＝7，则 tanθ＝（　　） C．1 D．2 【分析】利用两角和差的正切公式进行展开化简，结合一元二次方程的解法进行求解即 可． 【解答】解：由 2tanθ﹣tan（θ+ ）＝7，得 2tanθ﹣ ＝7， 即 2tanθ﹣2tan2θ﹣tanθ﹣1＝7﹣7tanθ， 得 2tan2θ﹣8tanθ+8＝0， 第 10 页（共 23 页） 即 tan2θ﹣4tanθ+4＝0， 即（tanθ﹣2）2＝0， 则 tanθ＝2， 故选：D． 【点评】本题主要考查三角函数值的化简和求解，结合两角和差的正切公式以及配方法 是解决本题的关键．难度中等． 10．（5 分）若直线 l 与曲线 y＝ 和圆x2+y2＝ 都相切，则l 的方程为（　　） A．y＝2x+1 B．y＝2x+ C．y＝ x+1 D．y＝ x+ 【分析】根据直线 l 与圆 x2+y2＝ 相切，利用选项到圆心的距离等于半径，在将直线与 曲线 y＝ 求一解可得答案； 【解答】解：直线 l 与圆 x2+y2＝ 相切，那么直线到圆心（0，0）的距离等于半径 ，四个选项中，只有 A，D 满足题意； 对于 A 选项：y＝2x+1 与 y＝ 联立可得：2x﹣ +1＝0，此时：无解； 对于 D 选项：y＝ x+ 与 y＝ 联立可得：x﹣ + ＝0，此时解得 x＝1； ∴直线 l 与曲线 y＝ 和圆x2+y2＝ 都相切，方程为y＝ x+ 故选：D． ，【点评】本题考查直线与圆的位置关系，属于基础题，采用选项检验，排除思想做题， 有时事半功倍． 11．（5 分）设双曲线 C： ﹣＝1（a＞0，b＞0）的左、右焦点分别为 F1，F2，离心 率为 ．P 是 C 上一点，且 F1P⊥F2P．若△PF1F2 的面积为 4，则 a＝（　　） A．1 B．2 C．4 D．8 【分析】利用双曲线的定义，三角形的面积以及双曲线的离心率，转化求解 a 即可． 【解答】解：由题意，设 PF2＝m，PF1＝n，可得 m﹣n＝2a， ，m2+n2＝4c2，e＝ ，可得 4c2＝16+4a2，可得 5a2＝4+a2， 解得 a＝1． 第 11 页（共 23 页） 故选：A． 【点评】本题考查双曲线的简单性质的应用，双曲线的定义以及勾股定理的应用，考查 转化思想以及计算能力． 12．（5 分）已知 55＜84，134＜85．设 a＝log53，b＝log85，c＝log138，则（　　） A．a＜b＜c B．b＜a＜c C．b＜c＜a D．c＜a＜b 【分析】根据 ，可得a＜b，然后由 b＝log85＜0.8 和 c＝log138＞0.8，得到 c＞b，再确 定 a，b，c 的大小关系． 【解答】解：∵ ＝＝log53•log58＜ ＝＜1，∴ a＜b； ∵55＜84，∴5＜4log58，∴log58＞1.25，∴b＝log85＜0.8； ∵134＜85，∴4＜5log138，∴c＝log138＞0.8，∴c＞b， 综上，c＞b＞a． 故选：A． 【点评】本题考查了三个数大小的判断，指数对的运算和基本不等式的应用，考查了转 化思想，是基础题． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．（5 分）若 x，y 满足约束条件 则 z＝3x+2y 的最大值为　7　． 【分析】先根据约束条件画出可行域，再利用几何意义求最值，z＝3x+2y 表示直线在 y 轴上的截距的一半，只需求出可行域内直线在 y 轴上的截距最大值即可． 【解答】解：先根据约束条件画出可行域，由 解得 A（1，2）， 如图，当直线 z＝3x+2y 过点 A（1，2）时，目标函数在 y 轴上的截距取得最大值时，此 时 z 取得最大值， 即当 x＝1，y＝2 时，zmax＝3×1+2×2＝7． 故答案为：7． 第 12 页（共 23 页） 【点评】本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题． 14．（5 分）（x2+ ）6 的展开式中常数项是　240　（用数字作答）． 【分析】先求出二项式展开式的通项公式，再令 x 的幂指数等于 0，求得 r 的值，即可求 得展开式中的常数项的值． 【解答】解：由于（x2+ ）6 的展开式的通项公式为 Tr+1 ＝•2r•x12﹣3r ，令 12﹣3r＝0，求得 r＝4，故常数项的值等于 故答案为：240． •24＝240， 【点评】本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公 式，求展开式中某项的系数，属于基础题． 15．（5 分）已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的体积为　 π　． 【分析】易知圆锥内半径最大的球应为圆锥的内切球，作图，求得出该内切球的半径即 可求出球的体积． 【解答】解：因为圆锥内半径最大的球应该为该圆锥的内切球， 如图，圆锥母线 BS＝3，底面半径 BC＝1， 则其高 SC＝ ＝2 ，不妨设该内切球与母线 BS 切于点 D， 令 OD＝OC＝r，由△SOD∽△SBC，则 ＝，即＝，解得 r＝ ，第 13 页（共 23 页） V＝ πr3＝ π， π． 故答案为： 【点评】本题考查圆锥内切球，考查球的体积公式，数形结合思想，属于中档题． 16．（5 分）关于函数 f（x）＝sinx+ 有如下四个命题： ①f（x）的图象关于 y 轴对称． ②f（x）的图象关于原点对称． ③f（x）的图象关于直线 x＝ 对称． ④f（x）的最小值为 2． 其中所有真命题的序号是　②③　． 【分析】根据函数奇偶性的定义，对称性的判定，对称轴的求法，逐一判断即可． 【解答】解：对于①，由 sinx≠0 可得函数的定义域为{x|x≠kπ，k∈Z}，故定义域关于原 点对称，由 f（﹣x）＝sin（﹣x）+ 所以该函数为奇函数，关于原点对称，所以①错②对； 对于③，由 f（π﹣x）＝sin（π﹣x）+ ＝sinx+ x）关于 x＝ 对称，③对； ＝﹣sinx﹣ ＝﹣f（x）； ＝f（x），所以该函数 f（ 对于④，令 t＝sinx，则 t∈[﹣1，0）∪（0，1]，由双勾函数 g（t）＝t+ 的性质，可知， g（t）＝t+ ∈（﹣∞，﹣2]∪[2，+∞），所以 f（x）无最小值，④错； 故答案为：②③． 【点评】本题考查了函数的基本性质，奇偶性的判断，求函数的对称轴、值域，属于基 第 14 页（共 23 页） 础题． 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17～21 题为必考 题，每个试题考生都必须作答。第 22、23 题为选考题，考生根据要求作答。（一）必考题 ：共 60 分。 17．（12 分）设数列{an}满足 a1＝3，an+1＝3an﹣4n． （1）计算 a2，a3，猜想{an}的通项公式并加以证明； （2）求数列{2nan}的前 n 项和 Sn． 【分析】（1）利用数列的递推关系式求出 a2，a3，猜想{an}的通项公式，然后利用数学 归纳法证明即可． （2）化简数列的通项公式，利用错位相减法求解数列的前 n 项和 Sn． 【解答】解：（1）数列{an}满足 a1＝3，an+1＝3an﹣4n， 则 a2＝3a1﹣4＝5，a3＝3a2﹣4×2＝7，…， 猜想{an}的通项公式为 an＝2n+1． 证明如下：（i）当 n＝1，2，3 时，显然成立， （ii）假设 n＝k 时，ak＝2k+1（k∈N+）成立， 当 n＝k+1 时，ak+1＝3ak﹣4k＝3（2k+1）﹣4k＝2k+3＝2（k+1）+1，故 n＝k+1 时成立， 由（i）（ii）知，an＝2n+1，猜想成立， 所以{an}的通项公式 an＝2n+1． （2）令 bn＝2nan＝（2n+1）•2n，则数列{2nan}的前 n 项和 Sn＝3×21+5×22+…+（2n+1）2n，…① 两边同乘 2 得，2Sn＝3×22+5×23+…+（2n+1）2n+1，…② ①﹣②得，﹣Sn＝3×2+2×22+…+2×2n﹣（2n+1）2n+1 ＝6+ ﹣（2n+1）2n+1 ，所以 Sn＝（2n﹣1）2n+1+2． 【点评】本题考查数列的递推关系式的应用，数学归纳法和数列求和，考查了转化思想 和计算能力，属中档题． 18．（12 分）某学生兴趣小组随机调查了某市 100 天中每天的空气质量等级和当天到某公 园锻炼的人次，整理数据得到下表（单位：天）： 锻炼人次 [0，200] （200，400] （400，600] 第 15 页（共 23 页） 空气质量等级 1（优） 256716 10 725 12 82（良） 3（轻度污染） 4（中度污染） 20（1）分别估计该市一天的空气质量等级为 1，2，3，4 的概率； （2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值 为代表）； （3）若某天的空气质量等级为 1 或 2，则称这天“空气质量好”；若某天的空气质量等 级为 3 或 4，则称这天“空气质量不好”．根据所给数据，完成下面的 2×2 列联表，并 根据列联表，判断是否有 95%的把握认为一天中到该公园锻炼的人次与该市当天的空气 质量有关？ 人次≤400 人次＞400 空气质量好 空气质量不好 附：K2＝ P（K2≥k） 0.050 3.841 0.010 6.635 0.001 k10.828 【分析】（1）用频率估计概率，从而得到估计该市一天的空气质量等级为 1，2，3，4 的概率； （2）采用频率分布直方图估计样本平均值的方法可得得答案； （3）由公式 计算 k 的值，从而查表即可， 【解答】解：（1）该市一天的空气质量等级为 1 的概率为： ＝；该市一天的空气质量等级为 2 的概率为： 该市一天的空气质量等级为 3 的概率为： 该市一天的空气质量等级为 4 的概率为： ＝；＝＝；；第 16 页（共 23 页） （2）由题意可得：一天中到该公园锻炼的平均人次的估计值为： ＝100×0.20+300× 0.35+500×0.45＝350； （3）根据所给数据，可得下面的 2×2 列联表， 人次≤400 人次＞400 总计 70 空气质量好 空气质量不好 总计 33 22 55 37 830 45 100 由表中数据可得：K2＝ ＞3.841， ＝≈5.820 所以有 95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关． 【点评】本题考查了独立性检验与频率估计概率，估计平均值的求法，属于中档题． 19．（12 分）如图，在长方体 ABCD﹣A1B1C1D1 中，点 E，F 分别在棱 DD1，BB1 上，且 2DE ＝ED1，BF＝2FB1． （1）证明：点 C1 在平面 AEF 内； （2）若 AB＝2，AD＝1，AA1＝3，求二面角 A﹣EF﹣A1 的正弦值． 【分析】（1）在 AA1 上取点 M，使得 A1M＝2AM，连接 EM，B1M，EC1，FC1，由已知 证明四边形 B1FAM 和四边形 EDAM 都是平行四边形，可得 AF∥MB1，且 AF＝MB1，AD ∥ME，且 AD＝ME，进一步证明四边形 B1C1EM 为平行四边形，得到 EC1∥MB1，且 EC1 ＝MB1，结合 AF∥MB1，且 AF＝MB1，可得 AF∥EC1，且 AF＝EC1，则四边形 AFC1E 为平行四边形，从而得到点 C1 在平面 AEF 内； 第 17 页（共 23 页） （2）在长方体 ABCD﹣A1B1C1D1 中，以 C1 为坐标原点，分别以 C1D1，C1B1，C1C 所在 直线为 x，y，z 轴建立空间直角坐标系．分别求出平面 AEF 的一个法向量与平面 A1EF 的一个法向量，由两法向量所成角的余弦值可得二面角 A﹣EF﹣A1 的余弦值，再由同角 三角函数基本关系式求得二面角 A﹣EF﹣A1 的正弦值． 【解答】（1）证明：在 AA1 上取点 M，使得 A1M＝2AM，连接 EM，B1M，EC1，FC1， 在长方体 ABCD﹣A1B1C1D1 中，有 DD1∥AA1∥BB1，且 DD1＝AA1＝BB1． 又 2DE＝ED1，A1M＝2AM，BF＝2FB1，∴DE＝AM＝FB1． ∴四边形 B1FAM 和四边形 EDAM 都是平行四边形． ∴AF∥MB1，且 AF＝MB1，AD∥ME，且 AD＝ME． 又在长方体 ABCD﹣A1B1C1D1 中，有 AD∥B1C1，且 AD＝B1C1， ∴B1C1∥ME 且 B1C1＝ME，则四边形 B1C1EM 为平行四边形， ∴EC1∥MB1，且 EC1＝MB1， 又 AF∥MB1，且 AF＝MB1，∴AF∥EC1，且 AF＝EC1， 则四边形 AFC1E 为平行四边形， ∴点 C1 在平面 AEF 内； （2）解：在长方体 ABCD﹣A1B1C1D1 中，以 C1 为坐标原点， 分别以 C1D1，C1B1，C1C 所在直线为 x，y，z 轴建立空间直角坐标系． ∵AB＝2，AD＝1，AA1＝3，2DE＝ED1，BF＝2FB1， ∴A（2，1，3），B（2，0，2），F（0，1，1），A1（2，1，0）， 则，，．设平面 AEF 的一个法向量为 ．则，取 x1＝1，得 ；设平面 A1EF 的一个法向量为 ．则，取 x2＝1，得 ．∴cos＜ ＞＝ ＝．第 18 页（共 23 页） 设二面角 A﹣EF﹣A1 为 θ，则 sinθ＝ ∴二面角 A﹣EF﹣A1 的正弦值为 ．．【点评】本题考查平面的基本性质与推理，考查空间想象能力与思维能力，训练了利用 空间向量求解空间角，是中档题． 20．（12 分）已知椭圆 C： +＝1（0＜m＜5）的离心率为 ，A，B 分别为 C 的左 、右顶点． （1）求 C 的方程； （2）若点 P 在 C 上，点 Q 在直线 x＝6 上，且|BP|＝|BQ|，BP⊥BQ，求△APQ 的面积． 【分析】（1）根据 e＝ ，a2＝25，b2＝m2，代入计算 m2 的值，求出 C 的方程即可； （2）设出 P，Q 的坐标，得到关于 s，t，n 的方程组，求出 AP（8，1），AQ（11，2） ，从而求出△APQ 的面积． 【解答】解：（1）由 e＝ 得e2＝1﹣ ，即 ＝1﹣ ，∴m2＝ ，故 C 的方程是： +＝1； （2）由（1）A（﹣5，0），设 P（s，t），点 Q（6，n）， 根据对称性，只需考虑 n＞0 的情况， 第 19 页（共 23 页） 此时﹣5＜s＜5，0＜t≤ ，∵|BP|＝|BQ|，∴有（s﹣5）2+t2＝n2+1①， 又∵BP⊥BQ，∴s﹣5+nt＝0②， 又+＝1③， 联立①②③得 或，当则时，则 P（3，1），Q（6，2），而 A（﹣5，0）， ＝（8，1）， ＝（11，2）， ∴S△APQ＝ ＝ |8×2﹣11×1|＝ ， 同理可得当 时，S△APQ＝ ， 综上，△APQ 的面积是 ．【点评】本题考查求椭圆方程以及了直线和椭圆的关系，考查转化思想，是一道综合题． 21．（12 分）设函数 f（x）＝x3+bx+c，曲线 y＝f（x）在点（ ，f（ ））处的切线与y 轴垂直． （1）求 b； （2）若 f（x）有一个绝对值不大于 1 的零点，证明：f（x）所有零点的绝对值都不大于 1 ．【分析】（1）求出原函数的导函数，由题意可得 f′（ ）＝3× ，由此求 得 b 值； （2）设 x0 为 f（x）的一个零点，根据题意， ，且|x0|≤1，得到 ，由|x0|≤1，对 c（x）求导数，可得 c（x）在[﹣1，1]上的单调性，得到 ． 设x1 为 f （ x ） 的 零 点 ， 则 必 有 ，由此求得 x1 的范围得答案． ， 可 得 【解答】（1）解：由 f（x）＝x3+bx+c，得 f′（x）＝3×2+b， 第 20 页（共 23 页） ∴f′（ ）＝3× ，即 b＝﹣ ； （2）证明：设 x0 为 f（x）的一个零点，根据题意， ，且|x0|≤1 ，则，由|x0|≤1， （﹣1≤x≤1）， 令 c（x）＝ ∴c′（x）＝ ＝，当 x∈（﹣1，﹣ ）∪（ ，1）时，c′（x）＜0，当 x∈（﹣ 可知 c（x）在（﹣1，﹣ ），（ ，1）上单调递减，在（ ，，，）时，c′（x）＞0 ）上单调递增． 又 c（﹣1）＝ ，c（1）＝ ，c（ ）＝﹣ ，c（ ）＝ ∴．设 x1 为 f（x）的零点，则必有 ，即，∴，得﹣1≤x1≤1， 即|x1|≤1． ∴f（x）所有零点的绝对值都不大于 1． 【点评】本题考查利用导数研究过曲线上某点处的切线方程，考查函数零点与方程根的 关系，考查逻辑思维能力与推理论证能力，是中档题． （二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的 第一题计分。[选修 4-4：坐标系与参数方程]（10 分） 22．（10 分）在直角坐标系 xOy 中，曲线 C 的参数方程为 （t 为参数且 t≠1 ），C 与坐标轴交于 A，B 两点． （1）求|AB|； （2）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求直线 AB 的极坐标方程． 【分析】（1）可令 x＝0，求得 t，对应的 y；再令 y＝0，求得 t，对应的 x；再由两点的 第 21 页（共 23 页） 距离公式可得所求值； （2）运用直线的截距式方程可得直线 AB 的方程，再由由 x＝ρcosθ，y＝ρsinθ，可得所 求极坐标方程． 【解答】解：（1）当 x＝0 时，可得 t＝﹣2（1 舍去），代入 y＝2﹣3t+t2，可得 y＝2+6+4 ＝12， 当 y＝0 时，可得 t＝2（1 舍去），代入 x＝2﹣t﹣t2，可得 x＝2﹣2﹣4＝﹣4， 所以曲线 C 与坐标轴的交点为（﹣4，0），（0，12）， 则|AB|＝ ＝4 ；（2）由（1）可得直线 AB 过点（0，12），（﹣4，0）， 可得 AB 的方程为 ﹣ ＝1， 即为 3x﹣y+12＝0， 由 x＝ρcosθ，y＝ρsinθ， 可得直线 AB 的极坐标方程为 3ρcosθ﹣ρsinθ+12＝0． 【点评】本题考查曲线的参数方程的运用，考查直线方程的求法和两点的距离公式的运 用，考查极坐标方程和直角坐标方程的互化，属于基础题． [选修 4-5：不等式选讲]（10 分） 23．设 a，b，c∈R，a+b+c＝0，abc＝1． （1）证明：ab+bc+ca＜0； （2）用 max{a，b，c}表示 a，b，c 的最大值，证明：max{a，b，c}≥ ．【分析】（1）将 a+b+c＝0 平方之后，化简得到 2ab+2ac+2bc＝﹣（a2+b2+c2）＜0，即 可得证； （2）利用反证法，假设 a≤b＜0＜c＜ ，结合条件推出矛盾． 【解答】证明：（1）∵a+b+c＝0，∴（a+b+c）2＝0， ∴a2+b2+c2+2ab+2ac+2bc＝0， ∴2ab+2ac+2bc＝﹣（a2+b2+c2）， ∵abc＝1，∴a，b，c 均不为 0， ∴2ab+2ac+2bc＝﹣（a2+b2+c2）＜0， ∴ab+ac+bc＜0； 第 22 页（共 23 页） （2）不妨设 a≤b＜0＜c＜ ∵a+b+c＝0，∴﹣a﹣b＝c＜ ，则 ab＝ ＞，，而﹣a﹣b≥2 ＞＝＝＝，与假设矛盾， 故 max{a，b，c}≥ ．【点评】本题考查基本不等式的应用和利用综合法与反正法证明不等式，考查了转化思 想，属于中档题． 第 23 页（共 23 页）