2011年海南省高考文科数学试题及答案下载

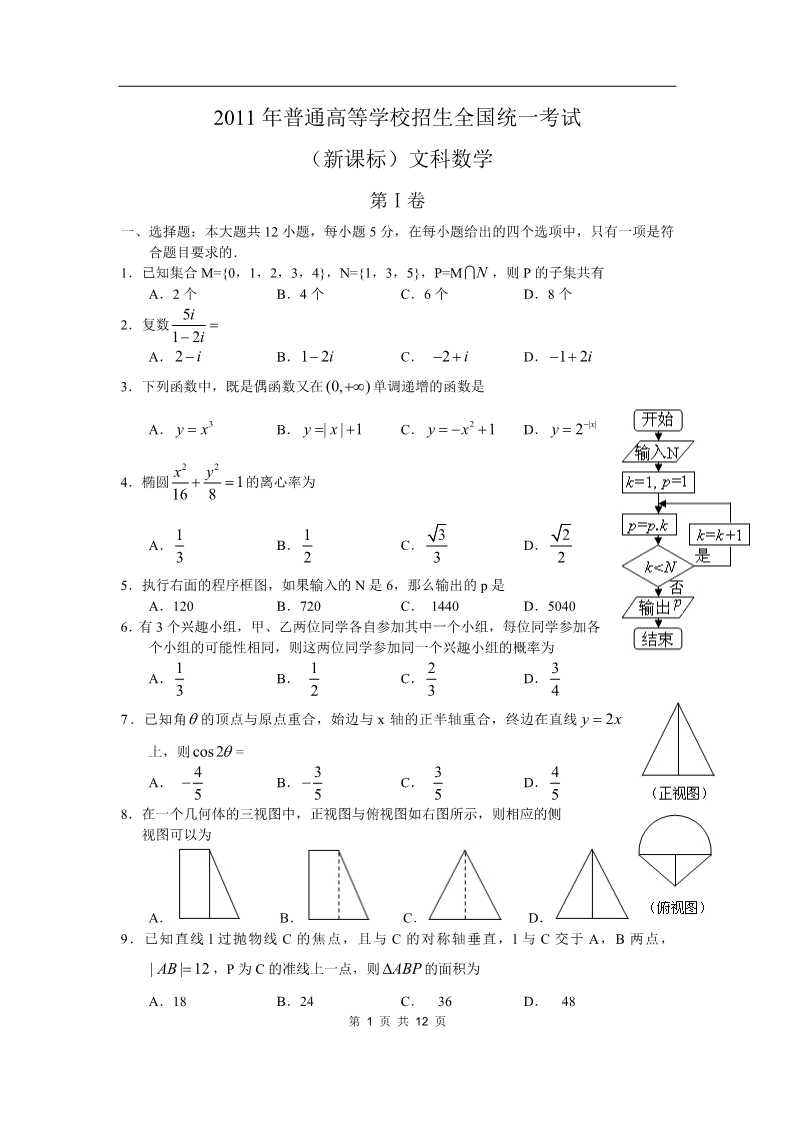
2011 年普通高等学校招生全国统一考试 （新课标）文科数学 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符 合题目要求的． 1．已知集合 M={0，1，2，3，4}，N={1，3，5}，P=M N ，则 P 的子集共有 A．2 个 5i B．4 个 C．6 个 D．8 个 2．复数 1 2i A． 2 i B．1 2i C． 2  i D． 1 2i 3．下列函数中，既是偶函数又在 (0,)单调递增的函数是 A． y  x3 B． y | x | 1 C． y  x2 1 D． y  2|x| x2 y2 4．椭圆 1的离心率为 16 811232A． B． C． D． 3325．执行右面的程序框图，如果输入的 N 是 6，那么输出的 p 是 A．120 B．720 C． 1440 D．5040 6．有 3 个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各 个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 13122334A． B． C． D． 7．已知角  的顶点与原点重合，始边与 x 轴的正半轴重合，终边在直线 y  2x 上，则 cos2 =4353545A． B． C． D． 58．在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧 视图可以为 A． B． C． D． 9．已知直线 l 过抛物线 C 的焦点，且与 C 的对称轴垂直，l 与 C 交于 A，B 两点， | AB |12 ，P 为 C 的准线上一点，则 ABP 的面积为 A．18 B．24 C． 36 D． 48 第 1 页 共 12 页 10．在下列区间中，函数 f (x)  ex  4x 3的零点所在的区间为 111 1 1 3 A． ( ,0) B． (0, ) C． ( , ) D． ( , ) 444 2 2 4 4411．设函数 f (x)  sin(2x  )  cos(2x  ) ，则 22224242A． y  f (x) B． y  f (x) C． y  f (x) D． y  f (x) 在在在在(0, )单调递增，其图象关于直线 x  对称 (0, )单调递增，其图象关于直线 x  对称 (0, )单调递减，其图象关于直线 x  对称 (0, )单调递减，其图象关于直线 x  对称 12．已知函数 y  f (x) 的周期为 2，当 x[1,1] 与函数 y | lg x |的图象的交点共有 时f (x)  x2 ，那么函数 y  f (x) 的图象 A．10 个 B．9 个 C．8 个 D．1 个 第Ⅱ卷 本卷包括必考题和选考题两部分．第 13 题-第 21 题为必考题，每个试题考生都必须做 答．第 22 题-第 24 题为选考题，考生根据要求做答． 二、填空题：本大题共 4 小题，每小题 5 分． 13．已知 a 与 b 为两个不共线的单位向量，k 为实数，若向量 a+b 与向量 ka-b 垂直，则 k=_____________． 3  2x  y  9 6  x  y  9 14．若变量 x，y 满足约束条件 ，则 z  x  2y 的最小值是_________． 15． ABC 中， B 120, AC  7, AB  5 ，则 ABC 的面积为_________． 16．已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底 3面面积是这个球面面积的 ，则这两个圆锥中，体积较小者的高与体积较大者的高的 16 比值为______________． 三、解答题：解答应写文字说明，证明过程或演算步骤． 17．（本小题满分 12 分） 113已知等比数列{an}中， a1  ，公比 q  ．31 an （I） Sn 为{an}的前 n 项和，证明： Sn  2（II）设bn  log3 a1  log3 a2  log3 an ，求数列{bn}的通项公式． 第 2 页 共 12 页 18．（本小题满分 12 分） 如 图 ， 四 棱 锥P  ABCD 中 ， 底 面ABCD 为 平 行 四 边 形 ，DAB  60 ，AB  2AD （I）证明： PA  BD （II）设 PD=AD=1，求棱锥 D-PBC 的高． ，PD  底面 ABCD． ；19．（本小题满分 12 分） 某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好，且质量指标值大于 或等于 102 的产品为优质品．现用两种新配方（分别称为 A 配方和 B 配方）做试验，各生 产了 100 件这种产品，并测量了每产品的质量指标值，得到时下面试验结果： A 配方的频数分布表 指标值分组 频数 [90，94） [94，98） [98，102） [102，106） [106，110] 820 42 22 8B 配方的频数分布表 指标值分组 频数 [90，94） [94，98） [98，102） [102，106） [106，110] 412 42 32 10 （I）分别估计用 A 配方，B 配方生产的产品的优质品率； （II）已知用 B 配方生产的一种产品利润 y（单位：元）与其质量指标值 t 的关系式为 2,t  94 y  2,94  t 102 4,t 102 估计用 B 配方生产的一件产品的利润大于 0 的概率，并求用 B 配方生产的上述 100 件 产品平均一件的利润． 20．（本小题满分 12 分） 在平面直角坐标系 xOy 中，曲线 y  x2  6x 1与坐标轴的交点都在圆 C 上． （I）求圆 C 的方程； （II）若圆 C 与直线 x  y  a  0交于 A，B 两点，且OA  OB, 求 a 的值． 第 3 页 共 12 页 21．（本小题满分 12 分） 已 知 函 数f (x)  aln x x 1 bx， 曲 线y  f (x) 在 点(1, f (1))处 的 切 线 方 程 为 x  2y 3  0 ．（I）求 a，b 的值； （II）证明：当 x>0，且 x 1时， f (x)  ln x ．x 1 请考生在第 22、23、24 三题中任选一题做答，如果多做，则按所做的第一题计分．做 答是用 2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑． 22．（本小题满分 10 分）选修 4-1：几何证明选讲 如图，D，E 分别为 ABC 的边 AB，AC 上的点，且不与 ABC 的顶点重合．已知 AE 的长为 m，AC 的长为 n，AD，AB 的长是关于 x 的方程 x2 14x  mn  0 的两个根． （I）证明：C，B，D，E 四点共圆； （II）若 A  90，且 m  4,n  6,求 C，B，D，E 所在圆的半径． 23．（本小题满分 10 分）选修 4-4：坐标系与参数方程 x  2cos 在直角坐标系 xOy 中，曲线 C1 的参数方程为 ( 为参数），M 为 C1 上 y  2  2sin   的动点，P 点满足OP  2OM ，点 P 的轨迹为曲线C2 （I）求 2 的方程； （II）在以 O 为极点，x 轴的正半轴为极轴的极坐标系中，射线  ．C3与C1 的异于极点 的交点为 A，与C2 的异于极点的交点为 B，求|AB|． 24．（本小题满分 10 分）选修 4-5：不等式选讲 设函数 f (x) | x  a | 3x，其中 a  0 ．（I）当 a=1 时，求不等式 f (x)  3x  2 的解集． 第 4 页 共 12 页 （II）若不等式 f (x)  0的解集为｛x| x  1}，求 a 的值． 参考答案 一、选择题 （1）B （2）C （3）B （4）D （5）B （6）A （7）B （8）D （9）C （10）C （11）D （12）A 二、填空题 15 3 41（13）1 （14）-6 （15） （16） 31．解析：本题考查交集和子集概念，属于容易题。显然 P= 1,3 ，子集数为 22=4 故选 B 2．解析：本题考查复数的运算，属容易题。 5i 5i 1 2i 解法一：直接法  2  i ，故选 C 1 2i 1 2i1 2i 解法二：验证法 验证每个选项与1-2i的积，正好等于 5i的便是答案。 3． 解析：本题考查函数的奇偶性和单调性，属于简单题 0, 的增函数，故选 B。 可以直接判断：A是奇函数，B是偶函数，又是 c2 2 424．解析;本题考查椭圆离心率的概念，属于容易题，直接求 e= ,故选 D。也 a228122 1 b 可以用公式  1  .e  故选 D。 ea2 5.解析：本题考查程序框图，属于容易题。 16 22可设 则 1 , 2 P1 K1  2，  3 P2 K,2  6，  4 P3 K,3  24，  5 P4 P5 K,4  120，  6 K,5 第 5 页 共 12 页  720，  7  6 P6 K,6 输出 720.故选 B 6.解析：本题考查古典概型，属于容易题。设三个兴趣小组分别为 A,B,C. 31他们参加情况共一下 9种情况，其中参加同一小组情况共 3中，故概率为  . 故选 A。 937.解析：本题考查三角公式，属于容易题。 135易知 tan =2，cos =.由 cos2 =2 2 -1= cos 5故选 B 8.解析：本题考查三视图的知识，同时考察空间想象能力。属于难题。 由正视图和俯视图可以判断此几何体前部分是一个的三棱锥，后面是一个圆锥，由此可 选 D 9.解析：本题考查抛物线的方程，属于中等题。 易知 2P=12，即 AB=12，三角形的高是 P=6，所以面积为 36，故选 C。 10.解析：本题考查零点存在定理，属于中等题。只需验证端点值，凡端点值异号就是答案。 故选 C。 11. 解析：本题考查三角函数的性质。属于中等题。 2π解法一：f(x)= 2sin(2x+ )= 2cos2x.所以 f(x) 在（0， ）单调递减，其图像关于直线 2πx = 对称。故选 D。 2π解法二：直接验证 由选项知（0， ）不是递增就是递减，而端点值又有意义，故只需验 2π证端点值，知递减，显然 x = 故选 D。 4不会是对称轴 12.解析：本题考查函数的图象和性质，属于难题。 本题可用图像法解。易知共 10 个交点 13. 解析：本题考查向量的基本运算和性质，属于容易题。 第 6 页 共 12 页 解法一：直接法 (a+b)(ka-b)=0展开易得 k=1. 解法二：凭经验 k=1时 a+b, a-b数量积为 0，易知 k=1. 14.解析：本题考查线性规划的基本知识，属于容易题。只需画出线性区域即可。 易得 z=x+2y的最小值为-6。 15.解析：本题考查余弦定理和面积公式，属于容易题。 0有余弦定理得 2  2  2  2AC  BC cos AC BC 120 AB 15 3 4所以 BC=3，有面积公式得 S= 16.解析：本题考查球内接圆锥问题，属于较难的题目。 3由圆锥底面面积是这个球面面积的 16  r2 3r3R3R 13得所以 ，则小圆锥的高为 ,大圆锥的高为 ，所以比值为 4 R2 三、解答题 16 R222（17）解： 1113n （Ⅰ）因为 an  ( )n1 .331313n 11(1 1 )1 3n Sn  ,231 an 所以 Sn  ,2（Ⅱ）bn  log3 a1  log3 a2  log3 an  (1 2  n) n(n 1)   2n(n 1) 所以{bn }的通项公式为bn   (18)解： .2（Ⅰ）因为 DAB  60, AB  2AD ， 由余弦定理 第 7 页 共 12 页 得BD  3AD 从而 BD2+AD2= AB2，故 BD AD PD BD PB，垂足为 E。已知 PD AD，又 BC//AD，所以 BC BD。 又 PD 所以 BD （Ⅱ）如图，作 DE 底面 ABCD，可得 BD 平面 PAD. 故 PA 底面 ABCD，则 PD BC。由（Ⅰ） 知 BD 故 BC 则 DE 平面 PBD，BC 平面 PBC。 DE。 由题设知，PD=1，则 BD= 3，PB=2， 3根据 BE·PB=PD·BD，得 DE= ，23即棱锥 D—PBC 的高为 .2（19）解 22 8 100 （Ⅰ）由试验结果知，用 A 配方生产的产品中优质的频率为 方生产的产品的优质品率的估计值为 0.3。 =0.3，所以用 A 配 32 10 100 由试验结果知，用 B 配方生产的产品中优质品的频率为 方生产的产品的优质品率的估计值为 0.42  0.42，所以用 B 配 （Ⅱ）由条件知用 B 配方生产的一件产品的利润大于 0 当且仅当其质量指标值 t≥94， 由试验结果知，质量指标值 t≥94 的频率为 0.96，所以用 B 配方生产的一件产品的利润 大于 0 的概率估计值为 0.96. 用 B 配方生产的产品平均一件的利润为 1 (4 (2)  54 2  42 4)  2.68（元） 100 (20）解： （ Ⅰ ） 曲 线y  x2  6x 1与 y 轴 的 交 点 为 （ 0 ， 1 ） ， 与x 轴 的 交 点 为 3  2 2,0),(3 2 2,0). （第 8 页 共 12 页 故可设 C 的圆心为（3，t），则有32  (t 1)2  (2 2)2  t2 , 解得 t=1. 则圆 C 的半径为 32  (t 1)2  3. 所以圆 C 的方程为 (x  3)2  (y 1)2  9. （Ⅱ）设 A（ x1, y1 ），B（ x2 , y2 ），其坐标满足方程组： x  y  a  0, (x  3)2  (y 1)2  9. 消去 y，得到方程 2×2  (2a  8)x  a2  2a 1  0. 由已知可得，判别式   56 16a  4a2  0. (8  2a)  56 16a  4a2 因此， x1,2 ,从而 4a2 0  2a 1 x1  x2  4  a, x1x2  ①2由于 OA⊥OB，可得 x1x2  y1 y2  0, y1  x1  a, y2  x2  a, 所以 又2x1x2  a(x1  x2 )  a2  0. ②由①，②得 a  1，满足   0, 故a  1. （21）解： x 1 (  ln x) bx2 x（Ⅰ） f ‘(x)  (x 1)2 f (1) 1, 1由于直线 x  2y 3  0的斜率为 ，且过点 (1,1) ，故 即12f ‘(1)  , 2b 1, 解得 a 1 ，b 1 。a 1b  , 2 2第 9 页 共 12 页 ln x 1（Ⅱ）由（Ⅰ）知 f (x)  ，所以 x 1 x x2 1 ln x 1f (x)  (2ln x  )1 x2 x 1 xx2 1 考虑函数 h(x)  2ln x  (x  0) ，则 x2x2  (x2 1) 2(x 1)2 h (x)    x2 x2 x所以当 x  1时， h (x)  0,而h(1)  0, 故1当当x (0,1) 时， h(x)  0,可得 h(x)  0; h(x)  0; 1 x2 1x (1,)时， h(x)  0,可得 ln x 1 x2 ln x 从而当 x  0,且x  1, f (x)   0,即f (x)  .x 1 x 1 （22）解： （I）连接 DE，根据题意在△ADE 和△ACB 中， AD×AB=mn=AE×AC， AD AE 即.又∠DAE=∠CAB，从而△ADE∽△ACB AC AB 因此∠ADE=∠ACB 所以 C，B，D，E 四点共圆。 （Ⅱ）m=4， n=6 时，方程 x2-14x+mn=0 的两根为 x1=2，x2=12. 故AD=2，AB=12. 取 CE 的中点 G，DB 的中点 F，分别过 G，F 作 AC，AB 的垂线，两垂线相交于 H 点， 连接 DH.因为 C，B，D，E 四点共圆，所以 C，B，D，E 四点所在圆的圆心为 H，半 径为 DH. 1由于∠A=900，故 GH∥AB， HF∥AC. HF=AG=5，DF= (12-2)=5. 2故 C，B，D，E 四点所在圆的半径为 5 2第 10 页 共 12 页 （23）解： （I）设 P(x，y)，则由条件知 M( X Y ,).由于 M 点在 C1 上，所以 2 2 x2y 2cos, x  4cos 即y  4  4sin  2  2sin 2 从而 C2 的参数方程为 x  4cos （为参数） y  4  4sin （Ⅱ）曲线 C1的极坐标方程为   4sin ，曲线 C2的极坐标方程为   8sin 。3333射线  射线  与与CC12的交点 的交点 AB的极径为 的极径为 .1 4sin  8sin ，2。所以| AB || 2  （24）解： （Ⅰ）当 a 1时， f (x)  3x  2 可化为 | x 1| 2 由此可得 x  3 故不等式 f (x)  3x  2 的解集为 1| 2 3 。或x  1 。{x | x  3 或x  1} 。(Ⅱ) 由 f (x)  0 x  a  3x  0 得此不等式化为不等式组 x  a x  a 或即x  a  3x  0 a  x  3x  0 第 11 页 共 12 页 aa因为 a  0 ，所以不等式组的解集为 x |x   ，由题设可得 =1，故 a  2 .22第 12 页 共 12 页