2009年山东省高考数学试卷(理科)word版试卷及解析下载

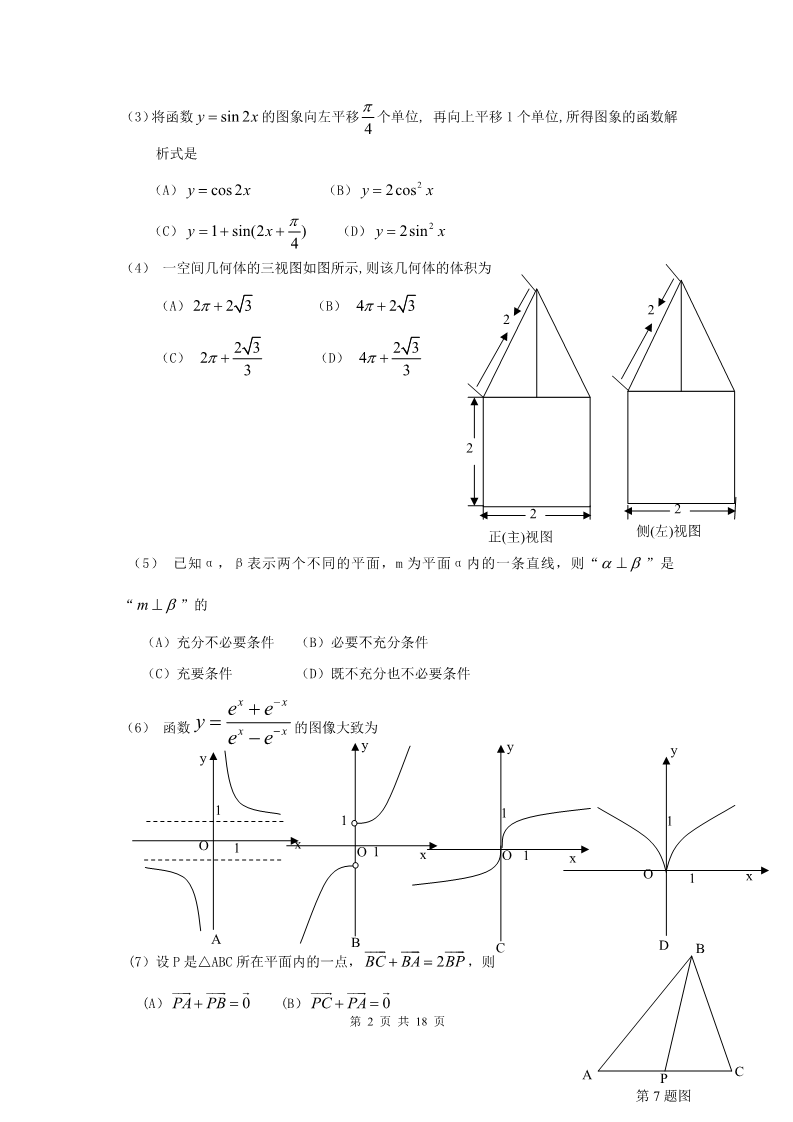
2009年普通高等学校招生全国统一考试(山东卷) 理 科 数 学 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共 4页，满分 150分，考试时间 120分钟。考试结束 后,将本试卷和答题卡一并交回. 注意事项： 1．答题前，考生务必用 0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类 填写在答题卡和试卷规定的位置上.，并将准考证号条形码粘贴在答题卡上指定位置。 2．第Ⅰ卷每小题选出答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上。 3．第Ⅱ卷必须用 0.5毫米黑色签字笔在答题卡各题的答题区域内作答;不能写在试题卷上; 如需改动，先画掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸,修正带, 不按以上要求作答的答案无效。 4．填空题请直接填写答案,解答题应写出文字说明,证明过程或演算步骤.。 参考公式： 柱体的体积公式 V=Sh，其中 S是柱体的底面积，h是锥体的高。 1锥体的体积公式 V= Sh ，其中 S是锥体的底面积，h是锥体的高。 3如果事件 A,B互斥,那么 P(A+B)=P(A)+P(B);R如果事件 A,B独立,那么 P(AB)=P(A)P(B). 事件 A在一次试验中发生的概率是 p ,那么 n 次独立重复试验中事件 A 次的概率:P (k)  Ck pk (1 p)nk (k  0,1,2,,n) . 第Ⅰ卷(共 60分) 恰好发生 knn一、选择题：本大题共 12小题，每小题 5分，共 60分。在每小题给出的四个选项中，只 有一项是符合题目要求的。 （1）集合 A  0,2,a ,B  1,a2 ,若 A B  0,1,2,4,16 ,则 a 的值为 （A）0 （B）1 （C）2 （D）4 3i 1i （2）复数 等于 （A）1 2i B）1 2i C） 2  i D） 2 i 第 1 页 共 18 页 4（3）将函数 y  sin 2x 的图象向左平移 个单位, 再向上平移 1个单位,所得图象的函数解 析式是 （A） y  cos2x （C） y  1 sin(2x  ) （B） y  2cos2 x （D） y  2sin2 x 4（4） 一空间几何体的三视图如图所示,则该几何体的体积为 （A） 2  2 3 2 3 （B） 4  2 3 222 3 （C） 2  （D） 4  33222侧(左)视图 正(主)视图 （5） 已知α，β表示两个不同的平面，m 为平面α内的一条直线，则“   ”是 “m   ”的 （A）充分不必要条件 （C）充要条件 （B）必要不充分条件 （D）既不充分也不必要条件 ex  ex （6） 函数 y  的图像大致为 yex  ex yyy1111xO11OxO1xOx1ABD   CB(7）设 P是△ABC所在平面内的一点， BC  BA  2BP ，则     (A） PA PB  0 (B） PC  PA  0 第 2 页 共 18 页 CAP第 7 题图      (C） PB  PC  0 (D） PA PB  PC  0 (８）某工厂对一批产品进行了抽样检测.有图是根据抽样检测 后的产品净重（单位：克）数据绘制的频率分布直方图，其中产 品净重的范围是[96，106]，样本数据分组为[96，98），[98，100), [100，102)，[102，104),[104，106],已知样本中产品净重小 于 100克的个数是 36，则样本中净重大于或等于 98克并且小于 104克的产品的个数是 频率/组距 0.150 0.125 0.100 0.075 0.050 (A）90 (B）75 (C） 60 (D）45 96 98 100 102 104 106 克x2 y2 第 8 题图 (9）设双曲线  1的一条渐近线与抛物线 y=x2 +1只有 a2 b2 一个公共点，则双曲线的离心率为 55(A） (B） 5 (C） (D） 5 42log (1 x), x  0 2(10） 定义在R上的函数 f(x)满足 f(x)= ，则 f（2009）的值 f (x 1)  f (x  2), x  0 为(A）-1 (B） 0 (C）1 (D） 2  x 21（11）在区间[-1，1]上随机取一个数 x， cos 的值介于 0到 之间的概率为( 2). 132122（A） （B） （C） （D） 33x  y  6  0 （12） 设x，y满足约束条件 x  y  2  0 ，x  0, y  0 x-y+2=0 y若目标函数 z=ax+by（a>0，b>0）的是最大值为 12， 23则的最小值为( ). a b 25 z=ax+by 8311 2（A） （B） （C） （D） 4 63-2 Ox23x-y-6=0 第 3 页 共 18 页 第Ⅱ卷（共 90分） 二、填空题：本大题共 4小题，每小题 4分，共 16分。 （13）不等式 2x 1  x  2  0 的解集为 （14）若函数 f(x)=ax -x-a(a>0且 a 1)有两个零 点，则实数 a的取值范围是 （15）执行右边的程序框图，输入的 T= .开始 ..S=0,T=0,n=0 （ 16）已 知 定 义 在R 上 的 奇 函 数f (x) ，满 足 f (x  4)   f (x),且在区间[0,2]上是增函数,若 是T>S 方程 f(x)=m(m>0) 在区间  8,8 上有四个不同的根 则否S=S+5 x1, x2 , x3, x4 ,输出 T x1  x2  x3  x4  _________. n=n+2 T=T+n 结束 三、解答题：本大题共 6分，共 74分。 （ 17 ） ( 本 小 题 满 分12 分 ) 设 函 数 f(x)=cos(2x+ )+sin2 x. 3(1)求函数 f(x)的最大值和最小正周期. 1C1(2)设 A,B,C为 ABC的三个内角，若 cosB= ，f( )=－ ，且C为锐角，求 sinA. 433第 4 页 共 18 页 （18）（本小题满分 12分） 如图，在直四棱柱 ABCD-A1 B1 C1 D1 中，底面 ABCD 为等腰梯形，AB//CD，AB=4, BC=CD=2, AA1 =2, E、E1 、F分别是棱 AD、AA1 、AB的中点。 D1 C1 （1） 证明：直线EE1 //平面 FCC1 ； A1 B1 （2） 求二面角B-FC1 -C的余弦值。 DE1 CEABF(19)(本小题满分 12分) 在某校组织的一次篮球定点投篮训练中，规定每人最多投 3次；在 A处每投进一球得 3 分，在 B处每投进一球得 2分；如果前两次得分之和超过 3分即停止投篮，否则投第三次， 某同学在 A处的命中率 q1 为 0.25，在 B处的命中率为 q2 ，该同学选择先在 A处投一球， 以后都在 B处投，用 表示该同学投篮训练结束后所得的总分，其分布列为 02345p0.03 （1） 求q2 的值； （2） 求随机变量 P1 P2 P3 P4 的数学期望 E ; （3） 试比较该同学选择都在B处投篮得分超过 3分与选择上述方式投篮得分超过 3分的 概率的大小。 第 5 页 共 18 页 （20）（本小题满分 12分） 等 比 数 列 { n }的 前n 项 和 为 aSn ， 已 知 对 任 意 的n N ， 点(n, Sn ) ， 均 在 函 数 y  bx  r(b  0 且b 1,b,r 均为常数)的图像上. （1）求 r的值； bn  2(log2 an 1)(n N ) （11）当 b=2时，记 b 1 b2 1 bn 1 bn 证明：对任意的 n N ，不等式 ·······  n 1 成立 1bb2 1（21）（本小题满分 12分） 两县城 A和 B相距 20km，现计划在两县城外以 AB为直径的半圆弧 上选择一点C建造垃 圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城 A和城 B的总影响度为 城 A与城 B的影响度之和，记 C点到城 A的距离为 xkm，建在 C处的垃圾处理厂对城 A和城 B的总影响度为 y,统计调查表明：垃圾处理厂对城 A的影响度与所选地点到城 A的距离的平 方成反比，比例系数为 4；对城 B的影响度与所选地点到城 B的距离的平方成反比，比例系 数为 k ,当垃圾处理厂建在 的中点时，对城A和城 B的总影响度为 0.065. （I）将 y表示成 x的函数； （Ⅱ）讨论（I）中函数的单调性，并判断弧 上是否存在一点，使建在此处的垃圾处理厂 对城 A和城 B的总影响度最小？若存在，求出该点到城 A的距离;若不存在，说明理由。 第 6 页 共 18 页 （22）（本小题满分 14分） x2 y2 设椭圆 E: 1（a,b>0）过 M（2， 2 ） ，N( 6 ,1)两点，O为坐标原点， a2 b2 （I）求椭圆 E的方程； （II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆 E恒有两个交点 A,B,且   OA  OB ？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。 第 7 页 共 18 页 2009 年高考数学山东理科解析 一、选择题 1【答案】 ．DA B  0,1,2,4,16 .,选D. 【解题关键点】因为 所以 a  4 2【答案】 ．C3  i (3  i)(1 i) 4 2i  2  i ，故选 C. 【解题关键点】因为 1 i (1 i)(1 i) 23．B【答案】 【 解 题 关 键 点 】 由 题 意 知 ： 平 移 后 的 函 数 解 析 式 为 42y  1 2sin 2(x  )  1 2sin(2x  ) ，2B. ，选  1 2cos2x  2cos x 4【答案】 ．C【解题关键点】由题意可知该几何体为一正四棱锥与一圆柱拼接而成的，所以改几何体的体 22积为这个圆柱的体积与这个正四棱锥的体积之和，其中圆柱的底面园直径为 ，高为 ，所 ，正四棱锥的测棱长为 ，底面正方形的对角线为 ，所以此正四棱锥 22以圆柱的体积为 2 1 2 2 2 3  22 1  ,C. 为故选 的体积 3235【答案】 ．Bm【解题关键点】由 为平面 内的一条直线且 m      得出 ；但是，反过来，若 m为平面 内的一条直线，则不一定有 m，还可能有 与平面 相交但不    m   且m //  m   、. B. 故选 垂直、 6【答案】 ．Aex  ex ex  ex B,C, D ,故选 【解题关键点】排除法：因为当 时，函数 无意义，故排除 x  0 y  第 8 页 共 18 页 A. 7【答案】 ．B.的中点， 即有 【解题关键点】因为 ，所以点 为，故 AC PBC  BA  2BP PC  PA  0 B. 选8【答案】 ．A【解题关键点】因为样品中产品净重小于 100 36 克的个数为 ，所以样本容量为 36  120 98 104 ，所以样本中产品净重大于或等于 克并且小于 克的个数为 2（0.05  0.1） A. ，故选 120（0..1 2  0.15 2  0.125 2） 90 9【答案】 ．Dx2 y2 bxay  【解题关键点】由题意知：双曲线 的一条渐近线为 ，由方程组  1 ax b2 by  xbby消去 ，得 x2  x 1  0   ( )2  4  0 有唯一解，所以 ，所以 a2aay  x 1 baca2  b2 b2D. ，故选  2,e   1 ( )  5 aaa10 ．C【答案】 f (1)  log 21, f (0)  0, f (1)  f (0)  f (1)  1 【解题关键点】由已知得 2f (2)  f (1)  f (0)  1, f (3)  f (2)  f (1)  1 (1)  0, f (4)  f (3)  f (2)  0  (1)  1, f (5)  f (4)  f (3)  1, f (6)  f (5)  f (4)  0, f (x) f (2009)  f (5)  1 6的值以 为周期重复性出现，所以 C所以函数 ，故选 11 ．A【答案】 x 2122x 233x 220  cos 1,1   【解题关键点】当 时，在区间 上，只有 或第 9 页 共 18 页 2213x  (1, )  ( ,1) .，即 ，根据几何概型的计算方法，这个概率值是 3312 ．A【答案】 【解题关键点】不等式表示的平面区域如图所示的阴影部分，由题意知： z  ax  by(a  0,b  0) x  y  2  0 当直线 过直线 与直线 3x  y  6  0 z  ax  by(a  0,b  0) 4,6 的交点 时，目标函数 ，即 12 取最大值 ，即 ，4a  6b  12 2a  3b  6 2323 2a  3b 13 ba13 25 6 (  )  (  )  2  而当，当且仅 abab6时取等号，故选 6ab6A . a  b 二、填空题 13 ．【答案】 （1，1） 22x 1  x  2 【解题关键点】原不等式等价于 ，两边平方并整理得： ，解得 3x  3 .1  x  1 14 ．【答案】 （1， ） x【 解 题 关 键 点 】函 数 f (x) 有 两 个 零 点 ，方 程 =()且a  0 a 1 a  x  a 有两个不相等的实数根，即两个函数 y  ax 与的图像有两个不同 xy  x  a a  x  a  0 的交点，当 时，两个函数的图像有且仅有一个交点，不合题意；当 时，两个 a  1 0  a  1 函数的图像有两个交点，满足题意 .15 ．30 【答案】 【解题关键点】由框图知， S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12; 第 10 页 共 18 页 S=20.n=8,T=12+8=20;S=25,n=10,T=20+10=30>S, 输出 T=30. 16 ．【答案】 8 f (x  4)   f (x) f (x  4)  f (x) f (0)  0 【解题关键点】因为定义在 上的奇函数，满足 R，所以 f (x) ， 所 以 ， 由 为 奇 函 数 ， 所 以 函 数 图 像 关 于 直 线 对 称 且 ， 由 x  2 f (x  4)   f (x) f (x  8)  f (x) 知f (x) 8，所以函数是以 为周期的周期函数，又因为 f (x) 0，2  2，0 在区间 上是增函数，所以 在区间 上也是增函数，如下图所示，那么方程 f (x)  m(m  0) x , x , x , x 4 ，不妨设 1x  x  x  x  8，8 在区间 上有四个不同的根 123234，由对称性知， x  x  4 x  x  x  x  8 x1  x2  4  (4)  (4)  12 .，，所以 341234三、解答题 17 ．【I答案】（）31312f(x)cos2(x )sin x cos2x sin2x (1cos2x) 222312，  sin 2x  21 3 ，最小正周期为 f (x) .当时，函数 的最大值为 ，得到 sin 2x  1 2C131233II f ( ) （ ） ==－C  ，又 为锐角，故 C，sinC sinC  242212 2 3cos B  sin B  32 33 1 1 22 22  3 .故sin A  sin(  B)     2323618 ．I【答案】解法一：（ ）在在直四棱柱 ABCD  A B C D 1111第 11 页 共 18 页 A B FFF C F 中，取 1 的中点 1 ，连结 ，1 由于 111FF // BB1 //CC F  FCC FCC C CFF A D 1 ，连结 ， 11 ，所以 平面 1 ，因此平面 1 即为平面 111// // CF 1 ，由于 ，CDA1F D1C1 CD 1A F CD CF // A D EAA 所以四边形 为平行四边形，因此 ，又因为 、分别是棱 、EAD 111111EE // A D CF // EE EE  FCC CF  ，FCC 平面 的中点，所以 ，所以 1 ，又因为 平面 1111111EE // FCC .1，所以直线 平面 1AB  4, BC  CD  2, F BF  BC  CF, BDF II （ ）因为 是棱 的中点，所以 为正三 1 平面 AB ABCD  A B C D CC 角形，取 的中点 ，则 O，又因为直四棱柱 1 中， CF OB  CF 111CC  BO OB  平面CC F FCC OP  C F ，所以 ，所以 ，过 在平面 O1 内作 ，ABCD 111B  FC  C 垂足为 ，连接 P，则为 二面角 的一个平面角，在 为正三角 OPB BCF BP 1OP OF RtCC F CC F 形中， ，在 中， ～，∵ OPF OB  3 11CC1 C1F 121214 BP  OP2  OB2   3  OP  2  ∴， 在 中 ， ，RtOPF 22  22 222OP BP 77214 cosOPB  B – FC C .，所以二面角 的余弦值为 1772AB  4, BC  CD  2, F :I解法二 （ ）因为 是棱 的中点 AB BF  BC  CF, BDF 所以 ，为正三角形，因为 为ABCD ,等腰梯形 所以 ,,M取的中点 BAC  ABC  60 AF 第 12 页 共 18 页 ,,所以 连接 以则，DM  CD DM DM  AB yxzDD 1 为 轴建立空间直 ,,为轴为轴DC DM ,角坐标系如图所示 0,0,0 则（）， ，，，C（0，2，0） DAF（ 3，1，0） （ 3，1，0） 31E（CE，，，所以 （0，2，2） ， ，0） （ 3，1，1） 1122    31,,CC F 设平面 的法 1CC1  (0,0,2) FC1  ( 3,1,2) CF  ( 3,1,0) EE1  ( , ,1) 22  nCF  0 3x  y  0 z  0 ,向 量 为 则  所 以 取则n  (x, y, z) n  (1, 3,0) nCC  0 1 ,所以直线   31,EE // FCC .平面 1所以 n  EE1 n EE1  1  3 10  0 122  n  FB  0   1II （ ） ,BFC ,则n1  (x1, y1, z1) 设 平 面 的 法 向 量 为 所 以 FB  (0,2,0)   1n  FC  0 11y1  0  ，取 ，则 n1  (2,0, 3)  3x  y  2z  0 111  ，nn1  21 30  0 3  2  222,，| n | 1 ( 3)  2 | n1 | 2  0  ( 3)  7     nn1 27  所以 cosn,n1  ,B – FC C ,为锐角 所以二 由图可知二面角 17| n || n1 | 2 7 第 13 页 共 18 页 7B – FC C .面角 的余弦值为 1719 ．I【答案】（ ）设该同学在处投中为事件 ,,处投中为事件 则事件 ,A B ,,在相互独立 AABBP(A)  0.25 ,,P(B)  q2 ,.且P(B) 1 q2 P(A)  0.75 :=0 时2 =0.03, 所以 1 q  0.2 根据分布列知 P(ABB)  P(A)P(B)P(B)  0.75(1 q2 ) 2q2  0.8 .II =2 ,时P=P(ABB  ABB)  P(ABB)  P(ABB) 1（） 当 1 q2 )2 1.5 q(，， 0.75  P(A)P(B)P(B)  P(A)P(B)P(B) 1 q2 2q2 () 0.24 2=3 =4 =5 ,,,P=P(ABB)  P(A)P(B)P(B)  0.25(1 q2 )  0.01 2当当当时时时；2P=； 0.48 P(ABB)  P(A)P(B)P(B)  0.75q2 3P=P(ABB  AB)  P(ABB)  P(AB) 4 P(A)P(B)P(B)  P(A)P(B)  0.25q2 (1 q2 )  0.25q2  0.24 所以随机变量 的分布列为 随机变量 的数学期望 E  00.03 20.24  30.01 40.48 50.24  3.63 .III 3（ ）该同学选择都在处投篮得分超过 分的概率为 BP(BBB  BBB  BB) 22 2(1 q )q  q  0.896 ； P(BBB)  P(BBB)  P(BB) 222I30.48+0.24=0.72. 因此该同学选择都在 处投篮得分超过 分的概率大于该同学选择第一次在 处投以后都 该同学选择（ ）中方式投篮得分超过分的概率为 3BA3 . 处投得分超过 分的概率 在B第 14 页 共 18 页 20 ．nI【答案】（ ）由题意知： .当时， Sn  b  r n  2 an  Sn  Sn1  bn  r  (bn1  r)  bn bn1  (b 1)bn1 ，由于 且b  0 b  1 ，所以当 a2  b ，，即 aa  S  b  r a2  b(b 1) {}时， 是以 为公比的等比数列，又 bn  2 n11a1 b(b 1) b  r  b .，解得 r  1 nII Sn  2 1 （ ） 当时， an  Sn  Sn1  (2n 1)  (2n1 1)  2n1 ，n  2 a1  S1  21 1  1 n1 an  2 又当时，，适合上式，，n 1 bn  2(log2 an 1)  2(log2 2n1 1)  2n b 1 b2 1 bn 1 35 72n 1     1······· ，bb2 bn 2 4 6 2n 1下面有数学归纳法来证明不等式： b 1 b2 1 bn 1 35 72n 1     1·······  n 1 bb2 bn 2 4 6 2n 13941证明：（ ）当 .右边，不等式成立 时，左边 n 1  2  2n  k(k  N*) 2（ ）假设当 时，不等式成立，即 b 1 b2 1 bk 1 35 72k 1     2 4 6 1·······  k 1 ，当时，左边n  k 1 bb2 bk 2k 1b 1 b2 1 bk 1 bk1 1 35 7     2 4 6 2k 1 2k  3 2k 2k  2 1······· ，bb2 bk bk1 12k  3 2k  2 (2k  3)2 4(k 1) 4(k 1)2  4(k 1) 1 4(k 1) 1 k 1  (k 1) 1  (k 1) 1 4(k 1) , . 时 不等式也成立 所以当 n  k 1 357（2n 1）  n 1  时，不等式 恒成立，所以对 12由（ ）、（ ）可得当 n N 2n 123n b 1 b2 1 bn 1 bn 1 ，不等式 ·······  n 1 成立 .任意的 n N bb2 1第 15 页 共 18 页 21 ．I,【答案】（ ）如右图 由题意知 4k22,y  (0  x  20) , BC  400  x AC  BC x2 400  x2 当垃圾处理厂建在弧 的中点时，垃圾处理厂到 、的距离都相等，且为 ，所 AB10 2km 4k0.065  以有 解得 ，(10 2)2 (10 2)2 ，k  9 49y  (0  x  20) x2 400  x2 89(2x) 18×4 8(400  x2 )2 x3 (400  x2 )2 49II （ ） y  ,y’   x2 400  x2 x3 (400  x2 )2 422y’  0 令，得 ，解得 ，即 ，x  640x 128000  0 x  160 x  4 10 49y  又 因 为 ， 所 以 函 数 在上 是 减 函 数 ， 在 x （0，4 10） 0  x  20 x2 400  x2 上是增函数， x （4 10，20） y时， 取得最小值， 当x  4 10 所以在弧 上存在一点，且此点到城市的距离为 A，使建在此处的垃圾 4 10km .处理厂对城市 A【解题关键点】 、的总影响度最小 B【结束】 22 ．x2 y2 【答案】（ ）椭圆 (a,b  0) I:2（ ， (,1) 两点， 6过）， NE1 M2a2 b2 42b2 1b2 1 1 2×2 y2 a，解得 a2  8,b2  4 ，所以椭圆 的方程为 .1 E6842aII （ ）假设存在该圆，满足条件，则要使得该圆的任意一条切线与椭圆恒有两个交点， 第 16 页 共 18 页 只该圆在椭圆内部，设该圆的方程为 x2  y2  r2 (r  4) ，则当直线 的斜率存在时， AB y  kx  m 2y2 y  kx  m 设该圆的切线方程为 ，解方程组 得x1 8422222,,x  2(kx  m)  8 即(1 2k )x  4kmx  2m 8  0 22222222,即则16k m  4(1 2k )(2m 8)  8(8k  m  4)  0   8k  m  4  0 4km x1  x2   1 2k2 ,2m2 8 1 2k2 x1x2  k2 (2m2 8) 4k2m2 m2 8k2 1 2k2 y1 y2  (kx1  m)(kx2  m)  k2 x1x2  km(x1  x2 )  m2   m2  1 2k2 1 2k2 2m2 8 m2 8k2   22x x y y 0 ,,,所以 ,要使 需使 即 0 3m 8k 8  0 OA  OB 121 2 1 2k2 1 2k2 23m2 8 m  2 82 6 3222,,m2  ,即所 以 又所 以 所 以 或k   0 8k  m  4  0 m  3m2  8 382 6 3y  kx  m ，因为直线 为圆心在原点的圆的一条切线，所以圆的半径为 m   m2 1 k2 m2 3m2 8 88r2  m1 k2 82 6 x2  y2  ,此时圆的切 r  ,,,所求的圆为 r  331 32 6 32 6 32 6 y  kx  m ,而当切线的斜率不存在时切线为 线都满足 或m  m   x   3×2 y2   满足 2 62 6 2 62 6 ,与椭圆 的两个交点为 或1 (, )( , )OA  OB 8433338(8k2  m2  4) (1 2k2 )2 2| AB | (x  x )2  y  y  (1 k2 )(x1  x2 )2  (1 k2 ) 2  12132 4k4  5k2 1 32 k2 ，[1 ]3 4k4  4k2 1 34k4  4k2 1 第 17 页 共 18 页 4 6 3,当时时，k  0 k  0 | AB | 32 1| AB | [1 ]当，134k2  4 k2 11810  4 69 4k2  4  8 ,故1因为 所以 AB   12  2 3 4k2  4 k2 38k2 m2 134 6 AB ,.当的斜率不存在时 AB  4 1 x2  y2   4 1 838综上，存在圆心在原点的圆 ，使得该圆的任意一条切线与椭圆 恒有两个交点 E34 6 3AB ,2 3 .,且的取值范围是 A B 第 18 页 共 18 页